McGraw Hill My Math Grade 4 Chapter 14 Review Answer Key

All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 14 Review will give you a clear idea of the concepts.

McGraw-Hill My Math Grade 4 Chapter 14 Review Answer Key

Vocabulary Check

Draw an example of each vocabulary word.

Question 1.
acute angle
Answer:

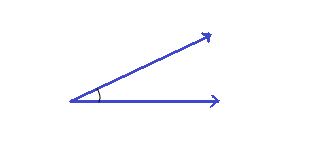
An angle that measures greater than 0° and less than 90° is called acute angle.

Question 2.
acute triangle
Answer:

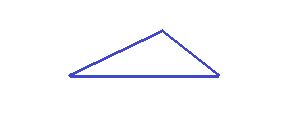
An acute triangle has three acute angles. You can observe this in the above figure.

Question 3.
Intersecting lines
Answer:

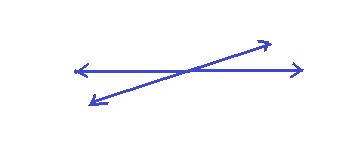
When two or more lines cross each other in a plane, they are called intersecting lines. The intersecting lines share a common point, which exists on all the intersecting lines, and is called the point of intersection.

Question 4.
line
Answer:

A line is a straight set of points that extends in opposite directions without ending. The line doesn’t have an endpoint. The length of the line cannot be measured. The line is represented as – AB and a horizontal line with arrow marks above the AB, i.e. \(\overleftrightarrow{A B}\).

Question 5.
line segment
Answer:

The line segment does not extend in both directions since it has a starting and an ending point. A line segment is part of a line between two endpoints. The length of the line segment can be measured. The line segment is denoted as – AB and a horizontal line above the AB, i.e. \(\overline{A B}\).

Question 6.
obtuse angle
Answer:

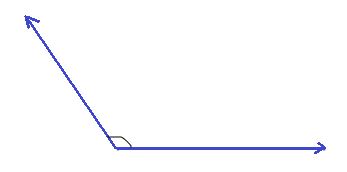
An angle measures greater than 90° but less than 180° is called Obtuse angle.

Question 7.
obtuse triangle
Answer:

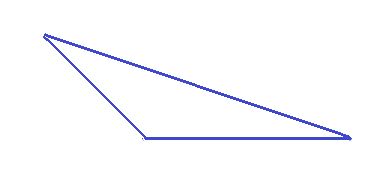
As you can observe the above figure, there is one obtuse angle, so the triangle is called as obtuse angled triangle.
The obtuse angle triangle cannot have perpendicular sides.

Question 8.
parallel lines
Answer:

The pairs of line segments that do not intersect or meet at any point are called parallel line segments. The lines are in a plane such that they are always the same distance apart and never meet, no matter how far they are extended.

Question 9.
perpendicular lines
Answer:

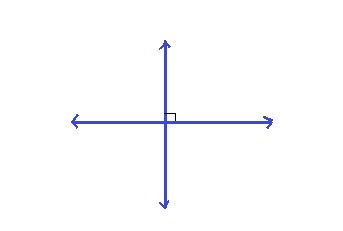
A straight line that forms a right angle (90 degrees) with another line is referred to as  perpendicular lines. In other words, two lines are said to be perpendicular to one another if they intersect at a right angle.

Question 10.
ray
Answer:

A ray is a part of a line that has one endpoint and extends in one direction without ending.

Question 11.
right triangle
Answer:

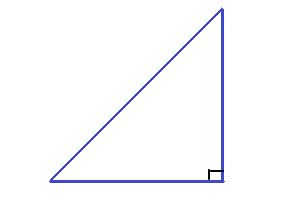
As you can observe the above figure, there is a 90 degrees angle, so the triangle is called as right angled triangle.
Only the pair of sides that form a right angle in right triangle are perpendicular to each other. Therefore, two sides are appear to be in perpendicular to each other.

Question 12.
line symmetry
Answer:

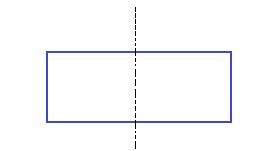
If a figure can be folded over a line so that one half of the figure matches the other half, it has line symmetry. The fold line indicating that a figure’s two halves match exactly is called Line of symmetry.
The dotted line here indicated the line of symmetry. If you fold the figure along the dotted line as shown above, the two halves of the folded part are symmetrical to each other.

Concept Check

Describe each figure. Use parallel, perpendicular, or intersecting. Use the most specific term.

Question 13.

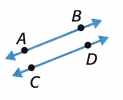
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are _____________.
Answer: Parallel lines
\(\overleftrightarrow{A B}\) and \(\overleftrightarrow{C D}\) are Parallel lines. AB and CD are two lines given in the figure.
The pairs of line segments that do not intersect or meet at any point are called parallel line segments. The lines are in a plane such that they are always the same distance apart and never meet, no matter how far they are extended.

Question 14.

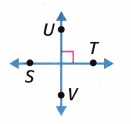
\(\overleftrightarrow{S T}\) and \(\overleftrightarrow{U V}\) are _____________.
Answer: Perpendicular lines
\(\overleftrightarrow{S T}\) and \(\overleftrightarrow{U V}\) are Perpendicular lines. Here, UV and ST are two lines. Both of them intersect each other at right angle (90 degrees) as shown in the figure.
A straight line that forms a right angle (90 degrees) with another line is referred to as  perpendicular lines. In other words, two lines are said to be perpendicular to one another if they intersect at a right angle.

Question 15.
Draw an angle with a measure greater than \(\frac{1}{4}\) turn.
Answer:

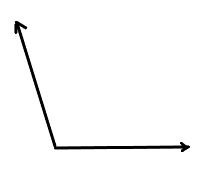
The above figure represents an angle which is greater than \(\frac{1}{4}\) turn. At first draw an horizontal ray from the imaginary point. Then, draw a ray as shown in the above figure to form an angle greater than \(\frac{1}{4}\) turn. The angle which is greater than \(\frac{1}{4}\) turn is treated as obtuse angle.

Question 16.
Classify the angle as right, acute, or obtuse.

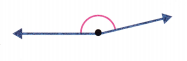
Answer: Obtuse angle
An angle measures greater than 90° but less than 180° is called Obtuse angle.

Question 17.
Classify the triangle as acute, right, or obtuse.

Answer: Obtuse triangle
As you can observe the above figure, there is one obtuse angle, so the triangle is called as obtuse angled triangle.
The obtuse angle triangle cannot have perpendicular sides.

Question 18.
Write the type of quadrilateral that best describes the shape at the right.

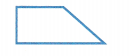
Answer: Trapezoid
Trapezoid is a type of quadrilateral, where it has one pair of parallel lines (i.e., opposite lines are parallel to each other).

Draw the line(s) of symmetry in each figure.

Question 19.

Answer:

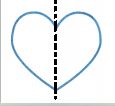
If a figure can be folded over a line so that one half of the figure matches the other half, it has line symmetry. The fold line indicating that a figure’s two halves match exactly is called Line of symmetry.
Here, in the above figure, we have 1 line of symmetry. The line of symmetry is indicated using a black line in the figure.

Question 20.

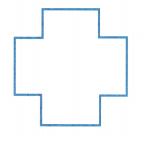
Answer:

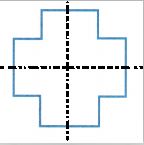
If a figure can be folded over a line so that one half of the figure matches the other half, it has line symmetry. The fold line indicating that a figure’s two halves match exactly is called Line of symmetry.
Here, in the above figure, we have 2 lines of symmetry. The line of symmetry is indicated using a black line in the figure.

Problem Solving

Question 21.
Brent started his homework at 4:00 P.M. He completed it at the time shown. Write how far the minute hand has turned in degrees and as a fraction of a full turn.

Answer: 90 degrees and \(\frac{90}{360}\) = \(\frac{1}{4}\)
The minutes hand is supposed to be on 12, but turned to be on 3. So, it minute hand has turned to 90 degrees.
A full turn is known as 360 degrees. In order to convert it into fraction, divide it with 360. Therefore, The minute hand has turned to \(\frac{90}{360}\) in fraction, which is \(\frac{1}{4}\) after simplification.

Question 22.
Sam draws a quadrilateral. It has one pair of parallel sides. What figure did Sam draw?
Answer: Trapezoid

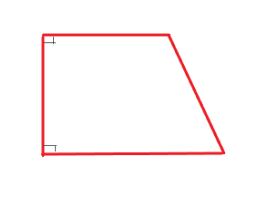
Trapezoid is a type of quadrilateral, where it has one pair of parallel lines (i.e., opposite lines are parallel to each other).

Question 23.
Sergio saw an angle that measures greater than 0° and less than 90°. What type of angle did he see?
Answer: Acute angle
An angle that measures greater than 0° and less than 90° is called acute angle.

Test Practice

Question 24.
Levi’s school is at the corner of High Street and Second Avenue. The corner forms a right angle. How might he describe the way the streets meet at his school?
(A) The streets are parallel.
(B) The streets are intersecting, but not perpendicular.
(C) The streets never meet.
(D) The streets are perpendicular.
Answer: D (The streets are perpendicular)
A straight line that forms a right angle (90 degrees) with another line is referred to as  perpendicular lines. In other words, two lines are said to be perpendicular to one another if they intersect at a right angle. So clearly, we can see that both the streets are perpendicular to each other.

Reflect

Use what you learned about geometry to complete the graphic organizer.

ESSENTIAL QUESTION
How are different ideas about geometry connected?

Now reflect on the ESSENTIAL QUESTION Write your answer below.
Answer:

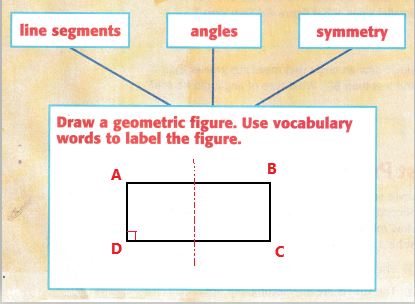
The above figure Rectangle can be illustrated as an example for line segments, angles and symmetry. The sides of the rectangle such as AB, BC, CD, DA act as line segments, which have two endpoints at the end. Each corner of the rectangle makes 90 degrees, which is a right angle. If a rectangle can be folded over a line so that one half of the figure matches the other half, it has line symmetry. The line of symmetry is indicated using a red line.
Line segments:
The line segment does not extend in both directions since it has a starting and an ending point. A line segment is part of a line between two endpoints. The length of the line segment can be measured. The line segment is denoted as – AB and a horizontal line above the AB, i.e. \(\overline{A B}\).
Angle:
An angle is a geometric shape that is formed when two rays have the same endpoint. The rotation of a ray’s beginning point to its endpoint is referred to as an angle. The amount of rotation from a ray’s initial point to its endpoint is measured as an angle. If the rotation is in the clockwise direction, the angle is said to be positive; if in the anticlockwise direction, it is said to be negative.
Angles are measured by the amount of rotation, or turning, from one ray to another. Angles are typically expressed in terms of degrees. A complete rotation in either a clockwise or counterclockwise direction, with the beginning and ending points being the same, is referred to as a degree. There are 360 parts in a rotation. It is said to be 1 degree if the rotation from the initial and ending side is \(\frac{1}{360}\)th of the rotation.
Symmetry:
If a figure can be folded over a line so that one half of the figure matches the other half, it has line symmetry. The fold line indicating that a figure’s two halves match exactly is called Line of symmetry.