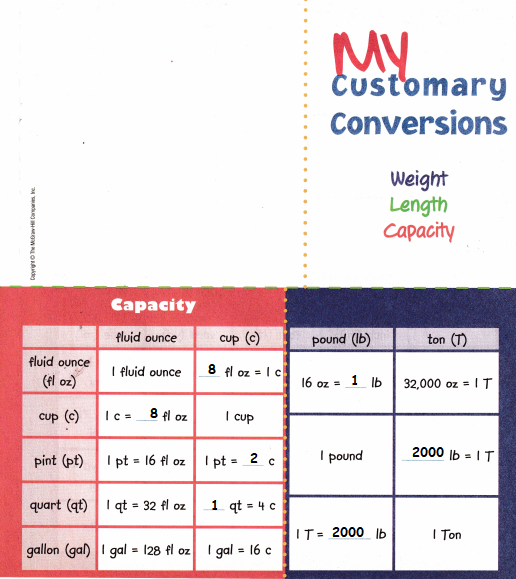
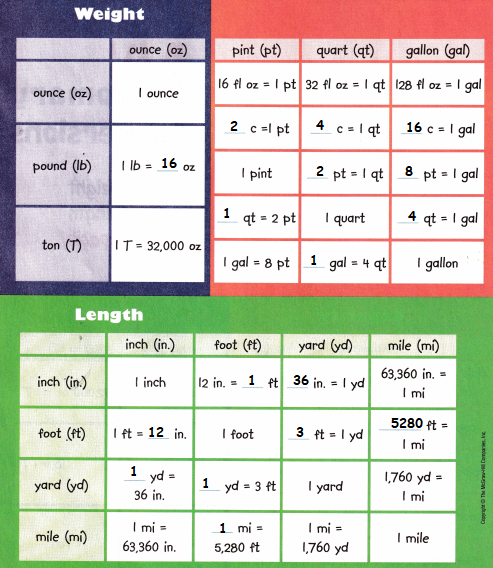
All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 11 Customary Measurement will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Chapter 11 Answer Key Customary Measurement
Essential Question
Why do we convert measurements?
Answer:
We must convert one unit to another in order to ensure accuracy and prevent confusion in measurements.
For example, we cannot measure table in kilometer and distance in feet or inchres.
Am I Ready
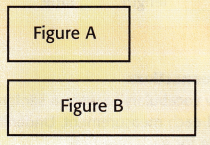
Circle the longer figure.
Question 1.
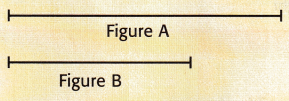
Answer:
From the given figures, we can observe that the Figure A is longer.
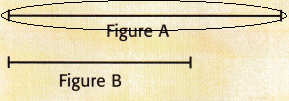
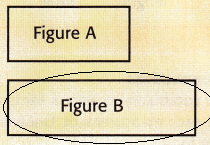
Question 2.
Answer:
From the given figures, we can observe that the Figure A is longer.
Multiply.
Question 3.
![]()
Answer:
Step 1: Multiply ones digit of the top number by the ones digit of the bottom number,which is 9×2=18 and carry the 1 over the 1. Now, the unit’s digit will be 8.
Step 2: Now mutiply tens digit of the top number by the ones digit of the bottom number, which is 9×1=9. Now, the tens digit will be 9+1=10. Now, the ten’s digit will be 10.
Final product will be 108
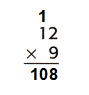
Question 4.
![]()
Answer:
Step 1: Multiply ones digit of the top number by the ones digit of the bottom number,which is 5×6=30 and carry the 3 over the 1. Now, the unit’s digit will be 0.
Step 2: Now mutiply tens digit of the top number by the ones digit of the bottom number, which is 5×1=5. Now, the tens digit will be 5+3=8. Now, the ten’s digit will be 8.
Final product will be 80
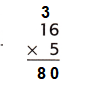
Question 5.
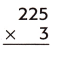
Answer:
Step 1: Multiply ones digit of the top number by the ones digit of the bottom number,which is 3×5=15 and carry the 1 over the 2. Now, the unit’s digit will be 5.
Step 2: Now mutiply tens digit of the top number by the ones digit of the bottom number, which is 3×2=6. Now, the tens digit will be 6+1=7. Now, the ten’s digit will be 7.
Step 3: Now mutiply tens digit of the top number by the ones digit of the bottom number, which is 3×2=6. Now, the tens digit will be 6. Now, the ten’s digit will be 6.
Final product will be 675
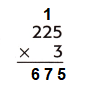
Add. Write in simplest form.
Question 6.
\(\frac{2}{10}\) + \(\frac{5}{10}\) = _____________
Answer:
Step 1: As the denominators of the given fraction is same, add the numerators directly.
Step 2: \(\frac{2}{10}\) + \(\frac{5}{10}\) = \(\frac{7}{10}\)
Thus, the sum of \(\frac{2}{10}\) + \(\frac{5}{10}\) equals \(\frac{7}{10}\)
Question 7.
\(\frac{1}{4}\) + \(\frac{1}{4}\) = ______________
Answer:
Step 1: As the denominators of the given fraction is same, add the numerators directly.
Step 2: \(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{2}{4}\)
Simplified fraction will be \(\frac{1}{2}\)
Thus, the sum of \(\frac{1}{4}\) + \(\frac{1}{4}\) equals \(\frac{1}{2}\)
Question 8.
\(\frac{1}{6}\) + \(\frac{3}{6}\) = ______________
Answer:
Step 1: As the denominators of the given fraction is same, add the numerators directly.
Step 2: \(\frac{1}{6}\) + \(\frac{3}{6}\) = \(\frac{4}{6}\)
Simplified fraction will be \(\frac{2}{3}\)
Thus, the sum of \(\frac{1}{6}\) + \(\frac{3}{6}\) equals \(\frac{2}{3}\)
Write the time shown on each clock.
Question 9.

Answer:
The small hand indicates hours and the large hand indicates minutes.
The hour hand is at 3 and the minutes hand is at 12.
Therefore, we can say it is 3’o clock.
Question 10.

Answer:
The small hand indicates hours and the large hand indicates minutes.
The hour hand is between 4 and 5. So, we say it as 4 hours.
The minute hand is eaxctly at 3, 3×5=15 minutes.
Therefore, we can say it as 15 minutes past 4.
Question 11.
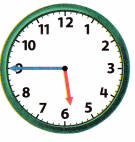
Answer:
The small hand indicates hours and the large hand indicates minutes.
The hour hand is between 5 and 6. So, we say it as 5 hours.
The minute hand is eaxctly at 9, 9×5=45 minutes.
Therefore, we can say it as 45 minutes past 5 or Quarter to 6.
My Math Words
Review Vocabulary
estimate
length
time
weight
Making Connections
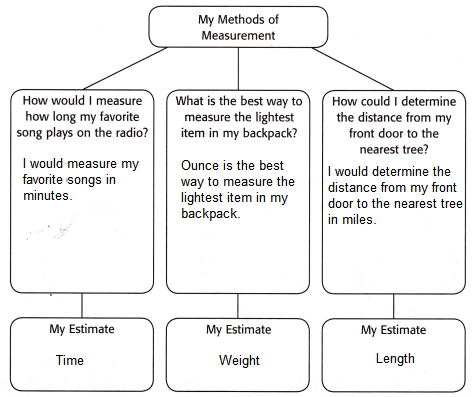
Use review vocabulary to write a sentence describing how you would find each measurement. Underline the word. Then provide an estimate for each question.
Answer:
My Vocabulary Cards

Ideas for Use
- Group 2 or 3 common words. Add a word that is unrelated to the group. Then work with a friend to name the unrelated word.
- Design a crossword puzzle. Use the definitions for the words as the clues,
To change to different units.
Which operation would you use to find the number of feet in 2 miles? Solve.
Answer:
1 mile equals 5280 feets.
So, to calculate the number of feet in 2 miles, we need to multiply the feet value with 2.
Multiply the ones digit of the top number by the ones digit of the bottom number, 2×0=0
Multiply the tens digit of the top number by the tens digit of the bottom number, 2×8=16. Carry 1 over 2.
Multiply the hundreds digit of the top number by the hundreds digit of the bottom number, 2×2=4, 4+1=5
Multiply the thousand digit of the top number by the thousand digit of the bottom number, 2×5=10
Final product will be 10560
5280×2=10560 feet.
The amount a container can hold.
Write a sentence describing the capacity of a bathtub.
Answer:
The capcity of a bathtub is 300 litres.It can hold upto 300 litres of water.
The units of measurement most often used in the United States, such as the inch, yard, and mile.
What customary unit of measurement would you use to describe the distance from California to New York?
Answer:
The customary unit of measurement used to describe the distance from California to New York will be mile.
A customary unit of capacity.
Write a sentence using the multiple-meaning word cup as a verb.
Answer:
She put down her cup of coffee and held the injured bird gently in her cupped hands.
A customary unit for measuring length.
This unit of length is based on the length of an adult’s foot. How could this information be useful?
Answer:
Foot is not a constant measurement. The size of the foot varies from person to person.
A customary unit of capacity.
Give examples of two things at the grocery store that are measured in fluid ounces.
Answer:
Oil and Milk are the two things at the grocery store that are measured in fluid ounces.
A diagram showing the frequency of data on a number line.
Describe what the line plot on the front of the card might represent.
Answer:
A line plot displays data on a number line. The number line displays the frequency of the data.
A customary unit of capacity.
Write a riddle to help you remember how many quarts, pints, and cups are in a gallon.
Answer:
A Gallon container has 4 Quarts of milk.
Each Quart has two pints of water.
Each Pint has 2 Cups of sugar in it.
In simple words, two “C’s” fit inside a “P,” two “P’s” fit inside a “Q,” and four “Q’s” fit inside a big, enormous “G.”

Ideas for Use
- Write a tally mark on each card every time you read the word in this chapter or use it in your writing. Challenge yourself to use at least 10 tally marks for each card.
- During this school year, create a separate stack of cards for key math verbs, such as convert. These verbs will help you in your problem solving.
A customary unit for measuring weight.
An 8-week old kitten weighs about 32 ounces. xplain if it is reasonable to weigh an adult cat in ounces.
Answer:
Since an ounce is a small unit of measurement, it can be used to determine the weight of a kitten. Adult cats shouldn’t be weighed in ounces; instead, they should be weighed in larger units of measurement like pounds.
A customary unit for measuring length.
It takes Tamika about 12 minutes to walk 1 mile. About how many minutes would it take Tamika to walk 3 miles?
Answer:
Tamika takes about 12 minutes to walk 1 mile.
Therefore, it will take 12×3=36 minutes to walk 3 miles.
A customary unit for measuring weight.
Estimate the weight of one of your textbooks to the nearest pound. Explain your reasoning.
Answer:
My maths textbook weighs around 1 pound.
A customary unit for measuring capacity.
1 pint = 2 cups
How many pints are in a quart? In a gallon?
Answer:
2 pints are in a quart.
8 pints are in a gallon.
A unit of time.
60 seconds = 1 minute
If there are 60 seconds in 1 minute, how many seconds are in 10 minutes?
Answer:
1 minute equals to 60 seconds.
10 minutes equals to 60×10=600 seconds.
A customary unit for measuring capacity.
Is 6 quarts greater than, less than, or equal to 2 gallons? Explain.
Answer:
1 gallon equals to 4 quarts.Thus, 2 gallons will be equal to 2×4=8 quarts.
Therefore, 6 quarts is less than 2 gallons.
A measurement that tells how heavy an object is.
Homophones are words that sounds alike, but are spelled differently. New and knew are homophones. Write a homophone for weight and its definition.
Answer:
The words “wait” and “weight” are homophones.
Wait means to stay and weight is used to tell how heavy an object is.
A customary unit for measuring weight.
What unit of weight would you use to measure a school desk? Explain.
Answer:
Pounds is the unit of weight used to measure a school desk. Pounds is used to measure the weight of heavy objects like desk.

Ideas for Use
- Pick a few lessons from the chapter. Write the name of each lesson on the front of the blank cards. Write a few study tips for each lesson on the back of each card.
- Have students use the blank cards to write summaries of the conversions they learned in the chapter.
A customary unit for measuring length.
Give examples of three things you might measure in yards.
Answer:
Examples of three things measured in yards are a classroom, a bus, and a door.
My Foldable
Follow the steps on the back to make your Foldable.
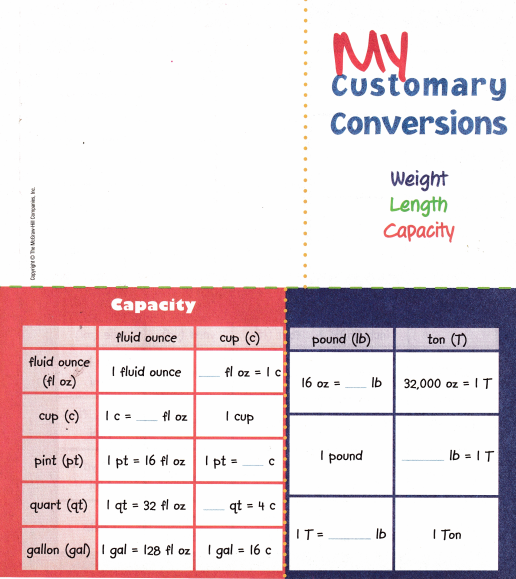
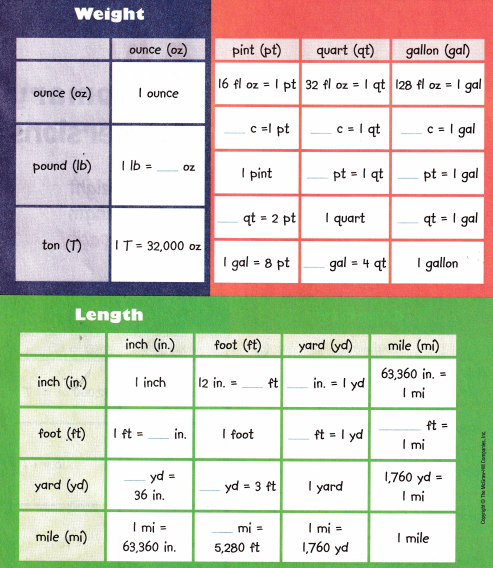
Answer: