All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 10 Review will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Chapter 10 Review Answer Key
Vocabulary Check
Question 1.
Write three examples of numbers that are decimals.
Write three examples of numbers that are not decimals.
Answer: 0.6, 0.11, 0.444 are examples of decimal numbers.
0.6 is 6 tenths, 0.11 is 1 tenth and 1 hundredths, 0.444 is 4 tenths, 4 hundredths, and 4 thousandths.
6, 11, 444 are examples of non decimal numbers, they are called Natural numbers.
Question 2.
Write three examples of decimals that have a 4 in the tenths place.
Answer: 0.4, 0.43, 0.432 are examples of decimals that have a 4 in the tenths place.
0.4 is 4 tenths, 0.43 is 4 tenths and 3 hundredths, 0.432 is 4 tenths, 3 hundredths, and 2 thousandths.
Question 3.
Write three examples of decimals that have a 5 in the hundredths place.
Answer: 0.15, 0.253, 0.959 are three examples of decimals that have a 5 in the hundredths place.
0.15 is 1 tenth and 5 hundredths, 0.253 is 2 tenths, 5 hundredths and 3 thousandths, 0.959 is 9 tenths, 5 hundredths, and 9 thousandths.
Concept Check
Write the decimal represented by each model.
Question 4.

Answer: 0.6
6 out of 10 boxes are in red color. So, if you divide 6 by 10, then 0.6 is the decimal number.
Question 5.

Answer: 0.05
5 out of 100 boxes are in red color. So, if you divide 5 by 100, then 0.05 is the decimal number.
Question 6.

Answer: 0.63
63 out of 100 boxes are in red color. So, if you divide 63 by 100, then 0.63 is the decimal number.
Shade the model. Then write the decimal.
Question 7.
four out of ten

Answer: 0.4
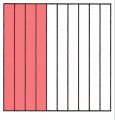
4 out of 10 boxes are in red color. So, if you divide 4 by 10, then 0.4 is the decimal number.
Question 8.
thirty-nine out of 100

Answer: 0.39

39 out of 100 boxes are in red color. So, if you divide 39 by 100, then 0.39 is the decimal number.
Question 9.
Write 0.8 as a fraction with a denominator of 10. Shade the grid.

0.8 = _________________
Answer: \(\frac{8}{10}\)
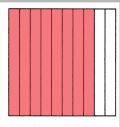
8 out of 10 boxes are in red color. So, if you divide 8 by 10, then 0.8 decimal number can be written as \(\frac{8}{10}\) in fractions.
Question 10.
Write 0.41 as a fraction with a denominator of 100. Shade the grid.

0.41 = ________________
Answer: \(\frac{41}{100}\)

41 out of 100 boxes are in red color. So, if you divide 41 by 100, then 0.41 decimal number can be written as \(\frac{41}{100}\) in fractions.
Write each fraction as an equivalent fraction with a denominator of 100. Then write the fraction as a decimal.
Question 11.
\(\frac{9}{10}\) = ________________
Decimal: _______________
Answer: \(\frac{9}{10}\) = \(\frac{90}{100}\)
Since 1 tenth is equal to 10 hundredths, 9 tenths is equal to 90 hundredths. You could also find the equivalent fraction by multiplying the numerator and denominator by 10.
\(\frac{9}{10}\) = 0.9 in decimal
Question 12.
\(\frac{3}{10}\) = _________________
Decimal: _________________
Answer: \(\frac{3}{10}\) = \(\frac{30}{100}\)
Since 1 tenth is equal to 10 hundredths, 3 tenths is equal to 30 hundredths. You could also find the equivalent fraction by multiplying the numerator and denominator by 10.
\(\frac{3}{10}\) = 0.3 in decimal
Add. Write each sum as a fraction with a denominator of 100 and as a decimal.
Question 13.
\(\frac{2}{10}\) + \(\frac{36}{100}\) = _______________
Answer: \(\frac{56}{100}\) = 0.56
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{2}{10}\) by 10. Then, it becomes \(\frac{20}{100}\)
Now, \(\frac{20}{100}\) + \(\frac{36}{100}\) = \(\frac{56}{100}\)
\(\frac{56}{100}\) = 0.56 in decimal
Question 14.
\(\frac{7}{10}\) + \(\frac{13}{100}\) = _________________
Answer: \(\frac{83}{100}\) = 0.83
In order to make the denominators of both fractions same for addition, multiply and divide \(\frac{7}{10}\) by 10. Then, it becomes \(\frac{70}{100}\)
Now, \(\frac{70}{100}\) + \(\frac{13}{100}\) = \(\frac{83}{100}\)
\(\frac{83}{100}\) = 0.83 in decimal
Order each set of decimals from greatest to least.
Question 15.
0.3, 0.23, 0.61 _____________
Answer: 0.61, 0.3, 0.23
0.61 > 0.3 > 0.23
whenever you are comparing the decimal numbers, first compare the digits in tenths place, followed by hundredths place, and then so on.
Question 16.
0.72, 0.5, 0.69 _______________
Answer: 0.72, 0.69, 0.5
0.72> 0.69 > 0.5
whenever you are comparing the decimal numbers, first compare the digits in tenths place, followed by hundredths place, and then so on.
Problem Solving
Question 17.
A barn has 10 animals. Three of the animals are horses. Write a decimal to show what part of the barn animals are horses.
Answer: 0.3
3 out of 10 animals in the barn or horses. So, if you divide 3 by 10, then 0.3 is the decimal number representing the part of horses.
Question 18.
Allison bought a snack using the coins shown. Write a decimal to show what part of a dollar she spent.

Answer: 0.27
nickel equals to 5 cents
penny equals 1 cent, there are total 2 pennies, so 2 cents
dime equals 10 cents, there are total 2 dimes, so 20 cents
Total = 5 + 2 + 20 = 27 cents
If you divide 27 cents by 100 cents, then 0.27 is the decimal number.
Question 19.
John lives 0.67 mile from the recreation center. Bella lives 0.8 mile from the recreation center. Who lives a greater distance from the recreation center? Explain.
Answer: Bella lives a greater distance from the recreation center, which is 0.8 mile
John lives 0.67 mile from the recreation center
Bella lives 0.8 mile from the recreation center
When you compare the distances of Bella and John, then 0.8 mile > 0.67 mile
whenever you are comparing the decimal numbers, first compare the digits in tenths place, followed by hundredths place, and then so on.
Question 20.
Joseph ran \(\frac{65}{100}\) mile in a race. Write a decimal to show what part of a mile Joseph ran.
Answer: 0.65
Joseph ran \(\frac{65}{100}\) mile in a race.
So, if you divide 65 by 100, then 0.65 is the decimal number that shows the part of a mile Joseph ran.
Test Practice
Question 21.
Chase poured three-tenths liter of lemonade and twenty-nine-hundredths liter of raspberry juice in a pitcher. Write the total amount of liquid Chase poured into the pitcher as a decimal.
(A) 0.32 liter
(B) 0.59 liter
(C) 0.69 liter
(D) 0.95 liter
Answer: B (0.59 liter)
three-tenths liter of lemonade, which is 0.3 in decimal
0.3 is equivalent to 0.30, which is 30 hundredths
twenty-nine-hundredths liter of raspberry juice, which is 0.29 in decimal
Therefore, total amount of liquid = lemonade + raspberry juice
= 0.30 + 0.29 = 0.59 liter
Reflect
Use what you learned about fractions and decimals to complete the graphic organizer.
Reflect on the ESSENTIAL QUESTION ? Write your answer below.
Answer:
