All the solutions provided in McGraw Hill My Math Grade 3 Answer Key PDF Chapter 9 Lesson 4 The Associative Property will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 3 Answer Key Chapter 9 Lesson 4 The Associative Property
The Associative Property of Multiplication states that the grouping of factors does not change the product.
Math in My World
Example 1
Chris and Katie each received 4 smile stickers a week for 3 weeks. How many smile stickers did they earn altogether?

Find the unknown in 2 × 3 × 4 = ____________.
When there are no parentheses, multiply in order from left to right. Or, use parentheses to group factors.
One Way
Multiply 2 and 3 first.
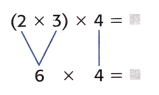
The unknown is 24.
Another Way:
Multiply 3 and 4 first.
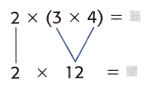
The unknown is 24.
Helpful Hint
The Associative Property also allows you to group the easier factors.
Either way 2 × 3 × 4 = _______________.
The _______________ Property shows that grouping does not change the product.
Answer: The Associative Property Property shows that grouping does not change the product.
Explanation:
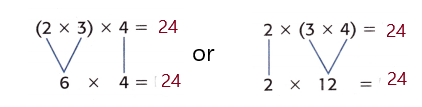
Given, 2 × 3 × 4
( 2 × 3 ) × 4
Multiply the factors inside the parentheses first.
6 × 3 = 24
So, 2 × ( 3 × 4 ) = 24
So, The Associative Property Property shows that grouping does not change the product.
Example 2
Cheryl has 2 photos. Each photo shows 5 friends holding the same number of flowers. There are 30 flowers altogether. How many flowers is each friend holding?

Write a multiplication sentence to help you find the missing factor.

So, 2 × 5 × 3 = ______________. Each friend is holding _____________ flowers.
Answer: 2 × 5 × 3 = 30 , Each friend is holding 30 flowers
Explanation:
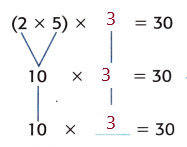
Given, ( 2 × 5 ) × 3
Multiply the factors inside the parentheses first.
10 × 3 = 30
So, 2 × ( 5 × 3 ) = 30.
Hence, Each friend is holding 30 flowers.
Talk Math
Explain how the Associative Property of Multiplication can help you find missing factors.

Answer: The associative property is a math rule that says that the way in which factors are grouped in a multiplication problem does not change the product.
Explanation:
For example, 7 ×(2 × 3) = (7 × 2) × 3 = 42.
So, The associative property is a math rule that says that the way in which factors are grouped in a multiplication problem does not change the product.
Guided Practice
Use parentheses to group two factors. Then find each product.
Question 1.
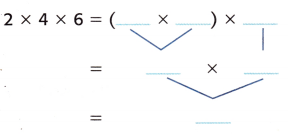
Answer: 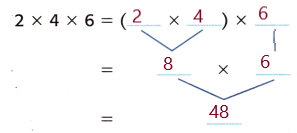
Explanation:
Given, 2 × 4 × 6
( 2 × 4 ) ×6
Multiply the factors inside the parentheses first.
8 × 6 = 48
So, 2 × ( 4 × 6 ) = 48.
Question 2.
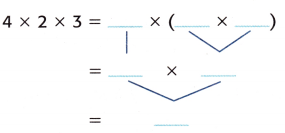
Answer: 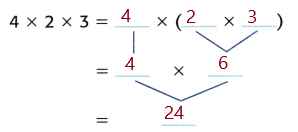
Explanation:
Given, 2 × 4 × 3
( 2 × 4 ) × 3
Multiply the factors inside the parentheses first.
8 × 3 = 24
So, 2 × ( 4 × 3 ) = 24.
Question 3.
Algebra Find the missing factor.
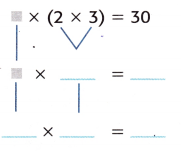
So, the unknown is ______________.
Answer: The unknown is 5
Explanation:
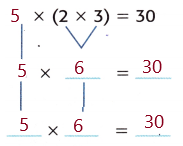
Given, ? × 2 × 3
( ? × 2 ) × 3
Let the unknown be 5
Multiply the factors inside the parentheses first.
5 × 2 × 3 = 30
So, 5 × ( 2 × 3 ) = 30.
Thus, The unknown is 5
Independent Practice
Use parentheses to group two factors. Then find each product.
Question 4.
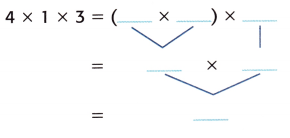
Answer: 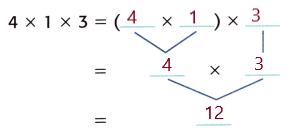
Explanation:
Given,4 × 1 × 3
(4 × 1 ) × 3
Multiply the factors inside the parentheses first.
4 × 3 = 12
So, 4 × ( 1 × 3 ) = 12.
Question 5.
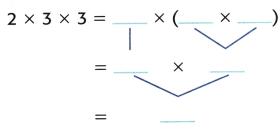
Answer: 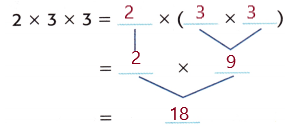
Explanation:
Given, 2 × 3 × 3
( 2 × 3 ) × 3
Multiply the factors inside the parentheses first.
6 × 3 = 18
So, 2 × ( 3 × 3 ) = 18.
Question 6.
6 × 2 × 2 = _____________
Answer: 6 × 2 × 2 = 24
Explanation:
Given, 6 × 2 × 2
( 6 × 2 ) × 2
Multiply the factors inside the parentheses first.
12 × 2 = 24
So, 6 × ( 2 × 2 ) = 24.
Question 7.
2 × 3 × 2 = ______________
Answer: 2 × 3 × 2 =12
Explanation:
Given, 2 × 3 × 2
( 2 × 3 ) × 2
Multiply the factors inside the parentheses first.
6 × 2 = 12
So, 2 × (3 × 2 ) = 12.
Algebra Find each missing factor.
Question 8.
(3 × ![]() ) × 4 = 24
) × 4 = 24
The unknown is ____________.
Answer: The unknown is 2
Explanation:
Given, (3 × ![]() ) × 4 = 24
) × 4 = 24
Let the unknown be y
3 × y × 4 = 24
y = \(\frac{24}{4 × 3}\)
y = 2
So, The unknown is 2.
Question 9.
(6 × ![]() ) × 5 = 30
) × 5 = 30
The unknown is ____________.
Answer: The unknown is 1
Explanation:
Given, (6 × ![]() ) × 5 = 30
) × 5 = 30
Let the unknown be y
6 × y × 5 = 30
y = \(\frac{30}{6 × 5}\)
y = 1
So, The unknown is 1.
Question 10.
![]() × (3 × 3) = 27
× (3 × 3) = 27
The unknown is ____________.
Answer: The unknown is 3.
Explanation:
Given, ![]() × (3 × 3) = 27
× (3 × 3) = 27
Let the unknown be y
y × 3 × 3 = 27
y = \(\frac{27}{3 × 3}\)
y = 3
So, The unknown is 3.
Question 11.
(2 × 5) × ![]() = 20
= 20
The unknown is ____________.
Answer: The unknown is 2
Explanation:
Given, (2 × 5) × ![]() = 20
= 20
Let the unknown be y
2 × 5 × y = 20
y = \(\frac{20}{2 × 5}\)
y = 2
So, The unknown is 2.
Algebra Find the value of each number sentence.
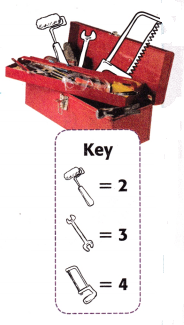
Question 12.
(6 × 1) × ![]() = ______________
= ______________
Answer: (6 × 1) × 2 =12
Explanation:
Given, figure value is 2
Then, (6 × 1) × 2
Multiply the factors inside the parentheses first.
6 × 2 = 12
So, 6 × ( 1 ×2 ) = 12.
Question 13.
4 × (![]() × 2) = ______________
× 2) = ______________
Answer: 4 × ( 3 × 2 ) = 24.
Explanation:
Given, figure value is 3
Then, ( 4 × 3 ) × 2
Multiply the factors inside the parentheses first.
12 × 3 = 24
So, 4 × ( 3 × 2 ) = 24.
Question 14.
![]() × (
× (![]() × 5) = _____________
× 5) = _____________
Answer: 4 × ( 2 × 5 ) = 40.
Explanation:
Given, figure value is 4 and 2
Then, ( 4 × 2 ) × 5
Multiply the factors inside the parentheses first.
8 × 5 = 40
So, 4 × ( 2 × 5 ) = 40.
Question 15.
(6 × ![]() ) × 3 = _______________
) × 3 = _______________
Answer: 6 × ( 2 × 3 ) = 36.
Explanation:
Given, figure value is 2
Then, ( 6 × 2 ) × 3
Multiply the factors inside the parentheses first.
12 × 3 = 36
So, 6 × ( 2 × 3 ) = 36.
Question 16.
![]() × (3 ×
× (3 × ![]() ) = _______________
) = _______________
Answer: 3 × ( 3 × 4 ) = 36.
Explanation:
Given, figure value is 3 and 4
Then, ( 3 × 3 ) ×4
Multiply the factors inside the parentheses first.
9 × 4 = 36
So, 3 × ( 3 × 4 ) = 36.
Question 17.
(5 × ![]() ) ×
) × ![]() = ______________
= ______________
Answer: 5 × ( 2 × 3 ) = 36.
Explanation:
Given, figure value is 2 and 3
Then, ( 5 × 2 ) ×3
Multiply the factors inside the parentheses first.
10 × 3 = 30
So, 5 × ( 2 × 3 ) = 36.
Problem Solving
Question 18.
Mathematical PRACTICE Make a Plan There are 5 apples. Troy cuts each apple into 2 pieces. Beth cuts each piece into 4 slices. What is the total number of apple slices?
Answer: There are 40 apple slices
Explanation:
Given, There are 5 apples. Troy cuts each apple into 2 pieces.
Beth cuts each piece into 4 slices.
That makes, 5 × ( 2 × 4 )
Multiply the factors inside the parentheses first.
10 × 4 = 40
So, 5 × ( 2 × 4 ) = 40
Hence, There are 40 apple slices.
Question 19.
Troy and Beth each cut 2 bananas into 4 pieces. What is the total number of banana pieces?
Answer: There are 16 banana pieces
Explanation:
Given, Troy and Beth each cut 2 bananas into 4 pieces.
That makes, 2 × 2 × 4
Multiply the factors inside the parentheses first.
4 ×4 = 16
So, 2 × ( 2 × 4 ) = 16.
Question 20.
A clerk unpacked 2 boxes of nails. Each box held 4 cartons with 10 packages of nails. How many packages of nails did the clerk unpack?
Answer: Clerk unpacked 80 packages of nails
Explanation:
Given, A clerk unpacked 2 boxes of nails. Each box held 4 cartons with 10 packages of nails.
That makes, 2 × ( 4 × 10 )
Multiply the factors inside the parentheses first.
8 × 10 = 80
So, 2 × ( 4 × 10 ) = 80.
Hence, Clerk unpacked 80 packages of nails.
HOT Problems
Question 21.
Mathematical PRACTICE Find the Error From the following, circle the number sentence that is not true. Explain.
(2 × 3) × 3 = 2 × (3 × 3)
3 × (1 × 5) = (3 × 1) × 5
4 × (4 × 2) = (3 × 4) × 4
6 × (4 × 2) = (6 × 4) × 2
Answer: 4 × (4 × 2) = (3 × 4) × 4 is not true
Explanation:
From the given question,
4 × (4 × 2) = (3 × 4) × 4 is not true, because
Here, not only the factors are grouped together
but also the numbers are changed as 2 as 3
So, 4 × (4 × 2) = (3 × 4) × 4 is not true
Question 22.
Building on the Essential Question Explain why the grouping of the factors does not matter when finding (3 × 4) × 2.
Answer: 24, Either way the result of the product is same.
Explanation:
Given, (3 × 4) × 2.
(3 × 4) × 2.
Multiply the factors inside the parentheses first.
12 × 2 = 24
or
3 × (4 × 2)
Group the same factors another way.
3 × 8 = 24
Either way the result of the product is same.
McGraw Hill My Math Grade 3 Chapter 9 Lesson 4 My Homework Answer Key
Practice
Use parentheses to group two factors. Then find each product.
Question 1.
2 × 3 × 6 = ______________
Answer: 2 × 3 × 6 = 36
Explanation:
Given, 2 × 3 × 6
( 2 × 3 ) ×6
Multiply the factors inside the parentheses first.
6 × 6 = 36
So, 2 × ( 3 × 6 ) = 36.
Question 2.
5 × 2 × 2 = ________________
Answer: 5 × 2 × 2 = 20
Explanation:
Given, 5 × 2 × 2
( 5 × 2 ) × 2
Multiply the factors inside the parentheses first.
10 × 2 = 20
So, 5 × ( 2 × 2 ) = 20.
Algebra Find each missing factor.
Question 3.
4 × (![]() × 4) = 32
× 4) = 32
The unknown is _____________.
Answer: The unknown is 2
Explanation:
Given, 4 × (![]() × 4) = 32
× 4) = 32
Let the unknown be y
4 × y × 4 = 32
y = \(\frac{32}{4 × 4}\)
y = 2
So, The unknown is 2.
Question 4.
(2 × ![]() ) × 6 =60
) × 6 =60
The unknown is ______________.
Answer: The unknown is 5.
Explanation:
Given, (2 × ![]() ) × 6 =60
) × 6 =60
Let the unknown be y
2 × y × 6 = 60
y = \(\frac{60}{2 × 6}\)
y =5
So, The unknown is 5.
Question 5.
(5 × ![]() ) × 1 = 45
) × 1 = 45
The unknown is _____________.
Answer: The unknown is 9.
Explanation:
Given, (5 × ![]() ) × 1 = 45
) × 1 = 45
Let the unknown be y
5 × y × 1 = 45
y = \(\frac{45}{5 × 1}\)
y =9
So, The unknown is 9.
Question 6.
![]() × (4 × 2) = 48
× (4 × 2) = 48
The unknown is _____________.
Answer: The unknown is 6.
Explanation:
Given, ![]() × (4 × 2) = 48
× (4 × 2) = 48
Let the unknown be y
4 × y × 2 = 48
y = \(\frac{48}{4 × 2}\)
y = 6
So, The unknown is 6.
Problem Solving
Question 7.
Mathematical PRACTICE Use Number Sense Mariette bought 4 packs of sparkling water. There were 6 bottles in each pack. If each bottle cost $2, how much did Mariette spend on sparkling water?
Answer: Mariette spend $48 on sparkling water.
Explanation:
Given, Mariette bought 4 packs of sparkling water.
There were 6 bottles in each pack. If each bottle cost $2,
that makes, 4 × ( 6 × 2 )
Multiply the factors inside the parentheses first.
4 × 12 = 48
So, ( 4 × 6 ) × 2 =48.
Hence, Mariette spend $48 on sparkling water.
Question 8.
Jamal and Brianna each bought 3 oranges. They sliced each orange into 6 pieces. How many orange slices did Jamal and Brianna have altogether?
Answer: Jamal and Brianna have altogether 36 orange slices.
Explanation:
Given, Jamal and Brianna each bought 3 oranges.
They sliced each orange into 6 pieces.
That makes, 2 × ( 3 × 6 )
Multiply the factors inside the parentheses first.
6 × 6 = 36
So, ( 2 × 3 ) × 6 = 36.
Hence, Jamal and Brianna have altogether 36 orange slices.
Question 9.
Mr. and Mrs. Perry packed their lunch 5 days in a row. Each of them packed 3 oatmeal cookies for dessert every day. What is the total number of cookies they packed for lunch that week?
Answer: The total number of cookies they packed for lunch that week is 30.
Explanation:
Given, Mr. and Mrs. Perry packed their lunch 5 days in a row.
Each of them packed 3 oatmeal cookies for dessert every day.
That makes, 2 × ( 5 × 3 )
Multiply the factors inside the parentheses first.
2 × 15 = 30
So, ( 2 × 5 ) × 3 = 30.
Hence, The total number of cookies they packed for lunch that week is 30.
Vocabulary Check
Question 10.
Write a definition for the Associative Property of Multiplication.
Answer: The associative property is a math rule that says that the way in which factors are grouped in a multiplication problem does not change the product.
Explanation:
For Example, ( 5 × 4 ) × 2 or 5 × ( 4 × 2 ).
Test Practice
Question 11.
What is the unknown in (3 × 3) × 7 = ![]()
(A) 21
(B) 30
(C) 42
(D) 63
Answer: D
Explanation:
Given, (3 × 3) × 7
Multiply the factors inside the parentheses first.
9 × 7 = 63
So, 3 × ( 3 × 7 ) = 63.
Hence, option D is correct.