All the solutions provided in McGraw Hill My Math Grade 3 Answer Key PDF Chapter 13 Lesson 9 Area and Perimeter will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 3 Answer Key Chapter 13 Lesson 9 Area and Perimeter
Two rectangles can have the same area but different perimeters.
Math in My World
Example 1
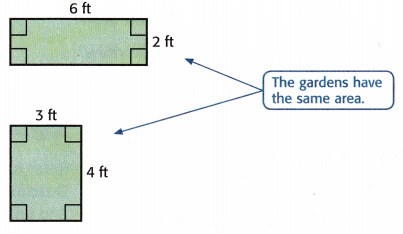
Elizabeth will build two fences, one surrounding each garden shown below. How much area does each garden cover? How much fencing will she need for each garden?

1. Find the area of each garden.
Garden 1
A = l × w
= 6 × 2
= ____________
Garden 2
A = l × w
= 4 × 3
= ____________
Answer:
Garden 1
A = l × w
= 6 × 2
= 12 sq. ft
Garden 2
A = l × w
= 4 × 3
= 12 sq. ft
The gardens have same area.
2. Find the perimeter of each garden.
Garden 1

Garden 1 needs ____________ feet of fencing.
Garden 2 needs ____________ feet of fencing.
Answer:
Garden 1
The perimeter is 6 + 2 + 6 + 2 = 16 ft
Garden 1 needs 16 feet of fencing.
Garden 2
The perimeter is 3 + 4 + 3 + 4 = 14 ft
Garden 2 needs 14 feet of fencing.
Example 2
Draw and label a rectangle that has the same perimeter as the rectangle shown, but a different area.
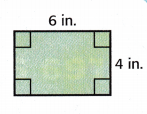
1. Find the perimeter and area of the rectangle shown.
The perimeter is 6 + 4 + 6 + 4, or ____________ inches.
The area is 6 × 4, or ____________ square inches. ← Multiply the length by the width.
2. Draw and label a rectangle that has a perimeter of 20 inches, but a different area.
What is the length of the rectangle you drew? ____________
What is the width of the rectangle you drew? ____________
What is the area of the rectangle you drew? ____________
Answer:
The perimeter is 6 + 4 + 6 + 4, or 2(6 + 4) = 20 inches.
The area is 6 × 4, or 24 square inches. ← Multiply the length by the width.
The length of the rectangle is 6 in.
The width of the rectangle is 4 in.
The area of the rectangle is 24 sq. inches
Talk Math
Refer to Example 2. Describe the length and width of a different rectangle you could have drawn.
Answer:
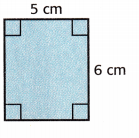
length = 5cm
width = 6 cm
Area = 5 × 6 = 30 sq. cm
Perimeter = 2(5 + 6) = 2 × 11 = 22 cm
Guided Practice
Question 1.
Describe the length and width of a rectangle that has the same area as the one below, but a different perimeter.
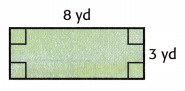
Answer:
length = 8yd
width = 3 yd
Area = 8 × 3 = 24 sq. yd
perimeter = 2(8 + 3) = 2 × 11 = 22 cm
Independent Practice
Draw and label a rectangle that has the same area, but a different perimeter, than each rectangle shown.
Question 2.

Answer:
length = 5cm
width = 6 cm
Area = 5 × 6 = 30 sq. cm
Perimeter = 2(5 + 6) = 2 × 11 = 22 cm
Question 3.
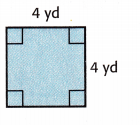
Answer:
s = 4 yd
Area = 4 × 4 = 16 sq. yd
Perimeter = 4 × 4 = 16 yd
Draw and label a rectangle that has the same perimeter, but a different area, than each rectangle shown.
Question 4.
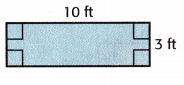
Answer:
l = 10ft
w = 3ft
A = 10 × 3 = 30sq. ft
P = 2(10 + 3) = 2 × 13 = 26 ft
Question 5.
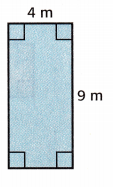
Answer:
l = 4 m
w = 9m
A = 4 × 9 = 36 sq. m
P = 2(4 + 9) = 2 × 13 = 26 m
Question 6.
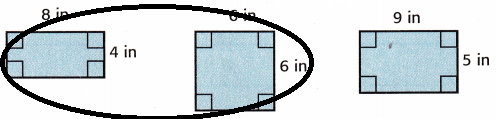
Circle the rectangles that have the same perimeter, but different areas.
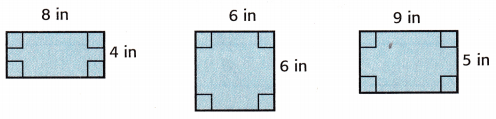
Answer:
P = 2(8 + 4) = 2 × 12 = 24
P = 4 × 6 = 24
P = 2(9 + 5) = 2 × 14 = 28
Problem Solving
William’s Windows makes the rectangular windows given in the table. Use this information to solve Exercises 7 and 8.
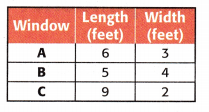
Question 7.
Mathematical PRACTICE Make Sense of Problems Which windows will use the same number of square feet of glass?
Answer:
Window A:
A = 6 × 3 = 18 sq. ft
Window B:
A = 5 × 4 = 20 sq. ft
Window C:
A = 9 × 2 = 18 sq. ft
Window A and C will use the same number of square feet of glass.
Question 8.
Each window will have a wood border surrounding it. Which windows will use the same amount of wood border?
Answer: Window A and C will use the same amount of wood border.
HOT Problems
Question 9.
Mathematical PRACTICE Which One Doesn’t Belong? Circle the rectangle that does not belong with the other two. Explain.

Answer:

Question 10.
Mathematical PRACTICE Reason What is true about the sum of the length and the width for any rectangles with the same perimeter, but different areas?
Answer:
All rectangles are also parallelograms, but not all parallelograms are rectangles. The perimeter P of a rectangle is given by the formula, P=2l+2w, where l is the length and w is the width of the rectangle. The area A of a rectangle is given by the formula, A=lw, where l is the length and w is the width.
Question 11.
Building on the Essential Question How can two rectangles with the same area have different perimeters?
Answer: Recognise that shapes with the same areas can have different perimeters and vice versa. It is not always the case that shapes with the same area have the same perimeter. Likewise, it is not always true that shapes with the same perimeter have equal area.
McGraw Hill My Math Grade 3 Chapter 13 Lesson 9 My Homework Answer Key
Practice
Question 1.
In the space at the right, draw and label a different rectangle that also has a perimeter of 16 meters, but a different area than shown above.
Answer:

P = 2(6 + 2)
P = 2 × 8 = 16 ft
A = 6 × 2 = 12 sq. ft
Draw and label a rectangle that has the same area, but a different perimeter, than each rectangle shown.
Question 2.
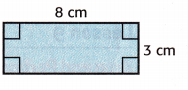
Answer:
A = 8 × 3
A = 24 sq. cm
P = 2(8 + 3) = 2 × 11 = 22 cm
Question 3.
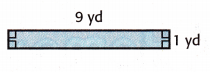
Answer:
A = 9 × 1 = 9 sq. yd
P = 2(9 + 1)
= 2 × 10 = 20 yd
Problem Solving
David’s Dog Pens makes the rectangular dog pens shown in the table. Use this information to solve Exercises 4 and 5.
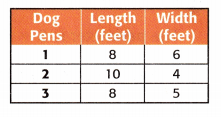
Question 4.
Which dog pens will take up the same area?
Answer:
Dog pens 1:
8 × 6 = 48 sq. ft
Dog pens 2:
10 × 4 = 40 sq. ft
Dog pens 3:
8 × 5 = 40 sq. ft
Dog pens 2 and 3 will take up the same area.
Question 5.
Which dog pens have the same perimeter?
Answer:
Dog pens 1:
2(8 + 6) = 2 × 14 = 28 ft
Dog pens 2:
2(10 + 4) = 2 × 14 = 28 ft
Dog pens 3:
2(8 + 5) = 2 × 13 = 26 ft
Thus, dog pens 1 and 2 have the same perimeter
Question 6.
Mathematical PRACTICE If Keep Trying Alexa drew a rectangle with an area of 36 square centimeters. The rectangle she drew has the smallest perimeter possible for this area. What is the length and width of the rectangle she drew?
Answer:
Alexa drew a rectangle with an area of 36 square centimeters.
P = 2(9 + 4)
= 2 × 13
= 26 cm
Length = 9
Width = 4 cm
Test Practice
Question 7.
Which rectangle has the same area as Rectangle E, but a different perimeter?
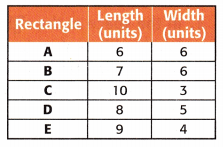
(A) Rectangle A
(B) Rectangle B
(C) Rectangle C
(D) Rectangle D
Answer:
Rectangle A:
A = 6 × 6 = 36 sq. units
P = 2(6 + 6) = 2 × 12 = 24 units
Rectangle B:
A = 7 × 6 = 42 sq. units
P = 2(7 + 6) = 2 × 13 = 26 units
Rectangle C:
A = 10 × 3 = 30 sq. units
P = 2(10 + 3) = 26 units
Rectangle D:
A = 8 × 5 = 40 sq. units
P = 2(8 + 5) = 2 × 13 = 26 units
Rectangle E:
A = 9 × 4 = 36 sq. units
P = 2(9 + 4) = 2 × 13 = 26 units
Rectangle A and E has same area but different perimeter.