Into Math Grade 8 Module 3 Lesson 3 Answer Key Apply Linear Equations

We included HMH Into Math Grade 8 Answer Key PDF Module 3 Lesson 3 Apply Linear Equations to make students experts in learning maths.

HMH Into Math Grade 8 Module 3 Lesson 3 Answer Key Apply Linear Equations

I Can solve linear equations and interpret solutions in context.

Step It Out
A. student service club is raising money through a “Loose Change competition among the grades. Jenaya brings in 20 coins, all of which are nickels and dimes, that have a total value of $1.30 to put in her grade’s bucket.
The equation 5(20 – d) + 10d = 130 can be solved to determine the number of dimes in Jenaya’s donation. How many dimes did Jenaya place in the bucket?

A. Apply the Distributive Property to the left side of the equation.
___ – ___ + 10d = 130
B. Combine like terms.
___ + ___ = 130
C. Solve the equation for d.
100 + 5d = 130

D. How many dimes does Jenaya place in the bucket? Write a sentence.
_____________
_____________
Answer: (complete answer for the above question)
The given equation:
5(20 – d) + 10d = 130
For step A:
Apply the distributive property.
(20 x 5) – (5 x d) + 10d = 130
100 – 5d + 10d = 130
For step B:
combine like terms:
“Like terms” are terms whose variables are the same.
100 + 5d = 130
For step C:
Now solve the equation for d.
5d = 130 – 100
5d = 30
d = 30/5
d = 6
For step D:
We got d = 6.
Therefore, Jenaya can place 6 dimes in the bucket.

Turn and Talk Which variable or expression represents the number of dimes? Which variable or expression represents the number of nickels? Explain your reasoning.

2. Grant needs to construct a rectangular garden with 55 feet of fencing around the perimeter. He draws a diagram to determine the length and width of the garden. What is the side length that Grant should choose for the garden?
A. How much fencing is needed for half of the garden, one length and one width?
___ feet
B. If the length of the garden is represented by l, how can you represent the width of the garden?
________________________
C. Label the sides of the garden.

D. Complete the equation that represents the perimeter of the garden.
2l + 2() =
E. What should be the first step in solving the equation? Why?
________________________
________________________
F. Complete the first step of solving the equation.
2l + ___ – ___ = 55
G. Combine the like terms on the left side of the equation and simplify.
________________________
H. What does this result mean about the solutions for l?
________________________
I. What does this result mean about the length of the garden?
________________________
________________________
Answer: [complete answer for the above question(2)]
For step A:
The number of feet of fencing = 55
for half of the garden, the fencing we need is:
Fencing = 55/2 = 27.5 feet
For step B:
The length of the garden is represented as ‘l’
The width of the garden is represented as ‘w’
For step C:

For step D:
The perimeter of a rectangle is the measure of the sum of its all sides which in the case of a rectangle are four sides in total.
The perimeter of rectangle formula = sum of all the four sides
The perimeter of the garden = P
P = 2l + 2w
2l + 2w = 55
For step E:
add -2w for both sides
For step F:
2l + 2w – 2w = 55 – 2w
For step G:
2l = 55 – 2w
divide both sides by 2
2l/2 = 55 – 2w/2
l = 55/2 – w
Therefore, the length of the garden is 55/2 – w

 

3. Pam and Rachel buy books at the bookstore where Rachel works. Each uses a coupon. As an employee Rachel pays only 75% of the advertised price after her coupon is applied. How many books could each purchase and spend the same amount for the same number of books?

A. Complete the equation to represent Rachel and Pam buying x books each and paying the same amount.
___ = 0.75 (___)
Answer:
Pam bought each book for $4
Rachel bought each book for $8
The number of books is x.
The equation would be:
4x + 8x = 0.75(4)
B. Solve the equation.
x = ___
Answer:
By continuing the part(A):
We need to find out the x value.
4x + 8x = 0.75(4)
12x = 3
x = 3/12
x = 1/4
C. Is it possible for Pam and Rachel to purchase x books and pay the same amount? Explain.
________________________
________________________
D. What does the solution to the equation represent about the situation?
________________________
________________________
________________________

Turn and Talk How would the solution be different if Rachel did not have a coupon?

Check Understanding

Question 1.
The equation x + (75.3 – x) = 75.3 represents the sum of two angle measures. How many possible combinations of angle measures satisfy these conditions?
Answer:
The above-given equation:
x + (75.3 – x) = 75.3
simplify both sides of the equation:
x + 75.3 − x = 75.3
75.3 = 75.3
subtract 75.3 from both sides
0 = 0
All real numbers are solutions.

Question 2.
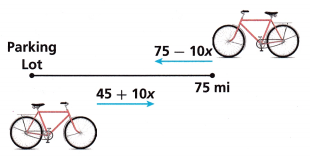
Two bicyclists on a 75-mile trail ride toward each other. One bicyclist begins at the 45-mile marker. The other begins at the end of the trail. The expressions shown represent the distance from the Parking Lot for each bicyclist when they meet.
A. Write an equation to represent the bicyclists’ meeting after x hours.
__________________
Answer:
75 – 10x = 45 + 10x
combine like terms
-10x – 10x = 45 – 75
-20x = -30
x = 30/20
x = 3/2 = 1.5 hours

B. After how many hours do the bicyclists meet?
__________________
Answer:
The bicyclist meet after 1 hour 5 minutes

C. How far away are the bicyclists from the parking lot when they meet?
__________________
Answer:

On Your Own

Question 3.
James rides down in an elevator that starts at a height of 120 feet. Brianne runs up the stairs from the ground floor.

Use the equation 120 – 2.5t = 1.5t to represent when James and Brianne are at the same height after t seconds.
A. Solve the equation.
____________________________________
Answer:
The above-given equation:
120 – 2.5t = 1.5t
get all like terms on one side
120 = 1.5t + 2.5t
120 = 4t
switching the sides
4t = 120
t = 120/4
t = 30

B. What does the solution represent about James and Brianne’s locations?
____________________________________
____________________________________
Answer:

C. What is their height above the ground floor when they are at the same height at the same time?
____________________________________
Answer:

Question 4.
The expression 100 – 2.5x represents the balance of Grace’s account after x days. The expression 100 + 2.5(5 – x) represents the balance of Tim’s account after x days. After how many days do the accounts have the same balance?
Answer:

Question 5.
Josh is 3 years older than Lynette. The sum of their ages is 49. Write expressions for Josh’s age and Lynette’s age, and use the expressions to write an equation relating their ages. Use the equation to determine Josh’s age and Lynette’s age.
Answer:
Josh = 3 + l
L = l
sum of thier ages = 49
The equation would be:
3 + l + l = 49
3 + 2l = 49
2l = 49 – 3
2l = 46
l = 46/2
l = 23
Hence, the age of Lynette is 23
Now find out josh age
Josh = 3 + l
josh = 3 + 23
josh = 26
Therefore, the age of Josh is 26.

Question 6.
Zander downloads a combination of 30 games and songs. He downloads 8 more songs than games. The equation g + (8 + g) = 30 can be solved to determine g, the number of games Zander downloaded. How many games did Zander download? How many songs did he download?
Answer:
The above-given equation:
g + (8 + g) = 30
combine like terms
2g+ 8 = 30
get all like terms on one side
2g = 30 – 8
2g = 22
g = 11
Therefore, 11 songs were downloaded.

Question 7.
Open Ended A business breaks even when its production costs are equal to its revenue. The expression 120 + 4x represents the cost of producing x items. Decide on a selling price for each item, and write an expression for the revenue generated by selling x items. How many items would you need to sell at your chosen price to break even? Write an equation and solve it.
Answer:

Question 8.
STEM A scientist conducts an experiment with two trees over many years. The shorter tree has fertilizer applied to it, and the taller tree does not. The shorter tree grows at an average rate of 8 inches per year. The taller tree grows at an average rate of 6 inches per year.
A. Complete the equation to represent the trees having the same height after t years:

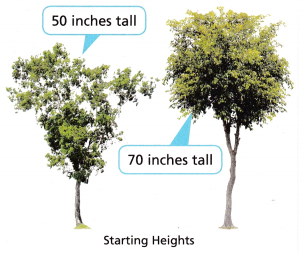
50 + 8t = ____
Answer:

B. After how many years will the heights of the two trees be equal?
__________________
Answer:

C. What will be the height of the trees when they are the same height?
Answer:

Question 9.
Rodney opens a savings account with $75 and also deposits $40 each month. Morgan opens an account with $50 and also deposits $40 each month. Will they have the same amount in their account at any point? If so, after how many months? Explain.
Answer:
The equation would be:
75(m + 40) = 50(m + 40)
75m + 3000 = 50m + 2000
75m – 50m = 2000 – 3000
25m = -1000
m = -1000/25
m = -40
There is no chance of having the same amount at any point.

Question 10.
Critique Reasoning Ethan said 5x – 20 = 5(x – 20) has infinitely many solutions. Is he correct? Explain.
Answer:
The above-given equation:
5x – 20 = 5(x – 20)
apply distributive property
5x – 20 = 5x – 100
combine like terms
5x – 5x = -100 + 20
0 = -80
Therefore, it has no solutions
Hence, Ethan statement is proved as wrong.

Question 11.
Abigail wants to find three consecutive even integers whose sum is four times the smallest of those integers. She lets n represent the smallest integer, then writes this equation: n + (n + 2) + (n + 4) = 4n.
A. Solve the equation.
__________________
Answer:
The given equation:
n + (n + 2) + (n + 4) = 4n.
3n + 6 = 4n
combine like terms
6 = 4n – 3n
6 = n
switch the sides
n = 6

B. What are the three integers?
__________________
Answer:
x, x+1, and x+2 are the three consecutive integers.

Question 12.
Every year Aiden uses income from his job to pay for 75% of his college tuition. Next year’s tuition will be $720 more than this year’s, and Alden will pay $2400. How much is this year’s tuition?
__________________
Answer:
Aiden uses his income to pay 75% of college tuition

Question 13.
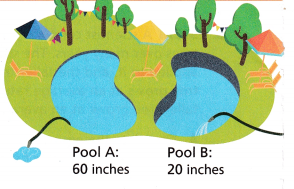
A model with Mathematics For Pool A, the water level is dropping 2.5 inches per hour. For Pool B, the water level increases 2.5 inches per hour. Starting water levels are shown. When will the pools have the same water level? Write an equation and solve.

Answer:

Question 14.
Isaac wants to play miniature golf. Go Golf charges $2.50 for ball and club rental and $4.25 per game. Golf Games charges $3.25 for ball and club rental and $8.50 for two games. For how many games would the cost be the same? Write and solve an equation to determine the number of games for which the cost would be the same.
Answer:

Question 15.
The members of a knitting club are buying supplies for their next meeting. For the club, they need to buy a new patterns book for $3.50. For each member, they need to buy a set of knitting needles for $3.20 and a ball of yarn for $5.40. They spent $63.70 in total. Write and solve an equation to determine how many members the knitting club has.
Answer:

Question 16.
Liam is a rewards member at a local restaurant. He can buy four tacos at the regular price and get $5.50 off his purchase. Zachary found a coupon to buy three tacos at the regular price and get $6.50 off his total. What would the taco price need to be in order for Liam and Zachary to spend the same amount?
A. Write the equation.
_____________
Answer:

B. Solve the equation.
_____________
Answer:

C. What does the solution to the equation represent?
_____________
Answer:

Lesson 3.3 More Practice/Homework

Apply Linear Equations

Question 1.
The expression 0.9(2x + 5) represents how much Stacy pays for x games of bowling at Lively Lanes. The expression 4.50 + 1.80x represents how much Parker pays for x games of bowling at Bowling and More. For how many games of bowling would they pay the same amount?

Answer:

Question 2.
Reason Janesa has 24 coins in her pocket worth exactly $1.00. She tells her younger brother Jackson that he can have the coins if he correctly guesses how many of each coin she has. She gives him the hint that there are only nickels and pennies.
A. Complete the equation that represents the total value of the nickels and p pennies:
5() + p = 100
Answer:

B. How many pennies does Janesa have in her pocket? _____________
Answer:

C. What is the total value of the pennies? _____
Answer:

D. What is the total value of the nickels? _____
Answer:

E. What should Jackson guess to get his sister’s coins?
__________________
Answer:

Question 3.
Math on the Spot Flex Gym charges a membership fee of $150.00 plus $40.50 per month to join the gym. A rival gym, Able Gym, charges a membership fee of $120.00 plus $46.75 per month. Find the number of months for which you would pay the same total fee to both gyms.
Answer:

Question 4.
Xin is getting an estimate from a printer for fliers for the drama club. Xin orders color prints and negotiates a 10% discount on the print job for the drama club. If f represents the number of fliers Xin orders, does 0.10(17.50 + 0.20f) represent the total cost of the print job? Why or why not?

Answer:

Test Prep

Question 5.
A biologist recorded the population growth of two species of frogs in a pond area starting in 2010. The first species started with 42 frogs and increased by 6 frogs per year. The second species started with 30 frogs and increased by 8 frogs per year.
A. Write an equation modeling equal populations of the frogs t years after 2010.
____________________________________
Answer:

B. In what year were the populations of the two groups of frogs equal?
____________________________________
Answer:

Use the information to answer Problems 6-7.

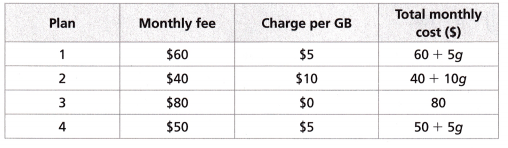
Riley is comparing cell phone plans. The table shows four options Riley is considering. The gigabytes of data used each month is represented by g.

Question 6.
Which two plans will never cost the same amount for any amount of data?
A. Plans 1 and 3
B. Plans 2 and 4
C. Plans 3 and 2
D. Plans 4 and 1
Answer:

Question 7.
Which plan should Riley get if he only uses 3 gigabytes of data each month?
A. Plan 1
B. Plan 2
C. Plan 3
D. Plan 4
Answer: Option D is correct.
Explanation:
Riley uses only 3GB and he will not use extra GB. So he would choose less amount with minimum GB.

Spiral Review

Question 8.
The segment with endpoints (0, 8) and (-6, 0) is dilated to a segment with endpoints (0, 6) and (-4.5, 0). What is the scale factor of the dilation?
Answer:

Question 9.
For what value of m does the equation 5 – 3x = m + mx have no solutions?
Answer:
The given equation:
5 – 3x = m + mx
Flip the equation:
m + mx = 5 – 3x
factor out variable m
m(x + 1) = -3x + 5
divide both sides by x+1
m(x +1)/x + 1 = -3x + 1/x + 5
m = -3x + 1/x + 5