Into Math Grade 8 Module 3 Lesson 2 Answer Key Examine Special Cases

We included HMH Into Math Grade 8 Answer Key PDF Module 3 Lesson 2 Examine Special Cases to make students experts in learning maths.

HMH Into Math Grade 8 Module 3 Lesson 2 Answer Key Examine Special Cases

I Can recognize linear equations that have no solution, one solution, or infinitely many solutions. I can determine if all the solutions of an equation with infinitely many solutions make sense in a real-world context. I can interpret the meaning of an equation with no solution in a real-world context.

Spark Your Learning
Leah and Mai are taking a card-making class. The teacher has 4 packs of blank cards and an additional 8 cards. Leah buys 4 packs of cards that each come with an additional 3 free cards in the pack. Mai buys 4 packs of cards that each come with an additional 2 free cards in the pack.

How many cards would need to be in each pack of cards so that the teacher had the same number of cards as Leah? as Mai?

Leah and Teacher
4(x + 3) = 4x + 8
Mai and Teacher
4(x + 2) = 4x + 8
What do you notice when you solve each equation? What do you think this means?

Answer:

It solved both equations.

Turn and Talk What do you think it means when an equation simplifies to an equation that is not true? Why?
Answer:
An equation that simplifies to an equation that is not true is called a false equation.

Build Understanding
You know that to solve an equation means to find the values for the variable that make a true statement. Sometimes an equation may have no solution or may not have a unique solution.

Just like a detective, you can gather clues to help you discover what will happen in each equation. Then you can gather clues in a table.

1. Solve the equation 2(\(\frac{x}{8}\) + 3) = 7 + \(\frac{1}{4}\)x.

Answer:
The above-given equation:
2(x/8 + 3) = 7 + 1/4x
solving the equation
subtract 1/4x from both sides
2(x/8 + 3) – 1/4x = 7 + 1/4x – 1/4x
if we simplify the above equation then we get
(2x/8 + 6) – 1/4 x = 7
x/4 + 6 – 1/4x = 7
6 = 7

A. What do you notice about the final equation?
_______________
Answer:
According to the above answer, we notice that the sides are not equal.
Hence, it has no solution.
B. Substitute several different values for x into the original equation. Simplify. Explain what happens.
_______________
Answer:
The above-given equation:
2(x/8 + 3) = 7 + 1/4x
If we substitute x = 1
2(1/8 + 3) = 7 + 1/4(1)
1/4 + 6 = 7 + 1/4
subtract 1/4 from both sides
1/4 + 6 – 1/4 = 7 + 1/4 – 1/4
6 = 7
No solution
If we substitute x = 2
2(x/8 + 3) = 7 + 1/4x
2(2/8 + 3) = 7 + 1/4(2)
If we simplify this we get:
2(1/4 + 3) = 7 + 1/2
2(1 + 12/4) = 14 + 1/2
2(13/4) = 15/2
13/2 = 15/2
The sides are not equal
hence, no solution.

C. How many solutions does the equation have? Use what you have discovered to fill in the table.

Answer:

Turn and Talk Write an equation with a variabìe x so that the equation is never true. Use addition on both sides of the equation.
Answer:
I would write the equation:
y + 1 = x + 2 (or) y = x + 2
For example if we take y = 1; x = 1
Now substitute the values in the equation.
1 + 1 = 1 + 2
2 = 3
Which is not true
If we take another example, y = 2; x = 3
2 + 1 = 3 + 1
3 = 4
which is not true.

2. Solve the equation x + 8 = 2(0.5x + 4).

A. What do you notice about the final equation?
___________________
Answer:
The above-given equation:
x + 8 = 2(0.5x + 4)
Steps:
x + 8 = x + 8
subtract 8 from both sides
x + 8 – 8 = x + 8 – 8
x = x
subtract x from both sides
x – x = x – x
0 = 0
We notice about the final equation is both sides are equal.
Hence, true for all x

Connect to Vocabulary
An equation that is true for all values of the variable has infinitely many solutions.

B. Substitute several different values for x into the original equation. Simplify. Explain what happens.
_____________________
_____________________
_____________________
Answer:
The above-given equation:
x + 8 = 2(0.5x + 4)
If we take x = 1
1 + 8 = 2(0.5 (1) + 4)
9 = (1) + 2(4)
9 = 1 + 8
9 = 9
It is true for all x
If we take x = 2
x + 8 = 2(0.5x + 4)
2 + 8 = 2(0.5(2) + 4)
10 = 2 + 8
10 = 10
It is true for all x.

C. How many solutions does the equation have? Use what you have discovered to fill in the table.

Answer:

D. Collect your information into one table.

Answer:

Turn and Talk What do you notice about equations that have no solution and equations that have infinitely many solutions? How are they alike or different?
Answer:
Having no solution means that an equation has no answer whereas infinite solutions of an equation mean that any value for the variable would make the equation true.

Step It Out

3. Use the simplified version of an equation to show how many solutions the equation has.
A. Jose draws an equilateral triangle with side length x. Marin draws an equilateral triangle with sides 2 inches longer. Marin writes an equation to show that her triangle has a perimeter that is 6 inches greater than Jose’s triangle. Solve the equation.

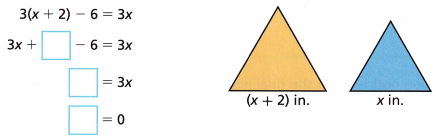
How many solutions does the equation have? Since the equation is always true, does it make sense that x could be a negative number?
___________________
___________________
___________________
Answer:
The above-given equation:
3(x + 2) – 6 = 3x
3x + 6 – 6 = 3x
3x = 3x
if we subtract 3x from both sides
3x – 3x = 3x – 3x
0 = 0
both sides are equal
true for all x.
Hence, x could not be a negative number.

B. Simplify the equation.
5.5x – 2.1 = 3 + 5.5x
5.5x – 2.1 – ___x = 3 + 5.5x – ___x
___ = ____
How many solutions does the equation have? What does the simplified equation mean?
Answer:
The above-given equation:
5.5x – 2.1 = 3 + 5.5x
subtract 5.5x from both sides
5.5x – 2.1 – 5.5x = 3 + 5.5x – 5.5x
if e simplify this, we get
-2.1 = 3
The sides are not equal
Therefore, the equation has no solution.

Check Understanding

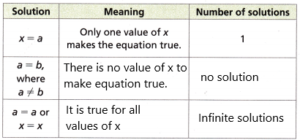
Question 1.
Brynne simplifies an equation and gets 2 = 3. What does this tell you about the equation?
Answer:
There is no value of x to make the equation true. So it has no solution.
The equation tells that it has no solution.
a is not equal to b.

Question 2.
Simplify the equation and tell whether the equation has one solution, no solution, or infinitely many solutions.
9(x + 5) = 20 + 9x + 25
Answer:
The above-given equation:
9(x + 5) = 20 + 9x + 25
simplification:
9x + 45 = 20 + 9x + 25
group like terms:
9x + 45 = 9x + 45
subtract 45 from both sides
9x + 45 – 45 =9x + 45 – 45
9x = 9x
subtract 9x from both sides
9x – 9x = 9x – 9x
0 = 0
both sides are equal.
It is true for all x.
hence, it has infinite solutions.

On Your Own

Question 3.
Lilly starts hiking along a trail at 3 miles per hour. Dave starts hiking the same trail from the same starting point at 3.5 miles per hour. If Lilly walked 2 miles before Dave started hiking, will he catch up to her? Write an equation to represent the situation and determine how many solutions the equation has.
Answer:
An application of linear equations can be found in distance problems. When solving distance problems we will use the relationship rt = d or rate (speed) times
time equals distance.
Lily – 3 miles per hour (rate)
Dave – 3.5 miles per hour (rate)
Time = 1 hour
if lily walked 2 miles before Dave started hiking
distance = 2 – D
distance  =D
The equation would be:
3(2 – D) = 3.5D
Multiply both sides by 10
3(2- D) . 10 = 3.5D . 10
30(2 – D) = 35D
60 – 30D = 35D
60 = 35D + 30D
60 = 65D
60/65 = D
12/13 = D
It has unique solution.

Question 4.
Maria pays a yearly fee of $3 to her swimming club and $2 per lesson. Carmen pays a yearly fee of $5 and $2 per lesson. After how many lessons will Maria and Carmen have paid the same amount? Write an equation and explain your answer.

Answer:

Question 5.
Construct Arguments Alex says that 3.2x – 5 = 3.2(x – 5) has infinitely many solutions. Is Alex correct? Explain why or why not.
Answer:
Alex is wrong.
Explanation:
The given equation:
3.2x – 5 = 3.2(x – 5)
Multiply both sides by 10
3.2x . 10 – 5 . 10 = 3.2(x – 5) . 10
32x – 50 = 32(x – 5)
32x – 50 = 32x – 160
add 50 to both sides
32x – 50 + 50 = 32x – 160 + 50
32x = 32x – 110
subtract 32x from both sides
32x – 32x = 32x – 110 -32x
0 = -110
Therefore, the sides are not equal
Hence, it has no solution.

Question 6.
Complete the equation so that it has infinitely many solutions.
2(2x + 1) = 2 + ____
Answer:
The above-given equation:
2(2x + 1) = 2 + ____
let the blank be 4x
2(2x + 1) = 2 + 4x
4x + 2 = 2 + 4x
subtract 2 from both sides
4x + 2 – 2 = 2 + 4x -2
4x = 4x
subtract 4x from both sides
4x – 4x = 4x – 4x
0 = 0
It is true for all values of x.
Hence, it has infinite solutions.

For Problems 7-11, determine whether each equation has one solution, no solution, or infinitely many solutions. If there is only one solution, find it.

Question 7.
\(\frac{1}{2}\)x + 3 – \(\frac{1}{4}\)x = 3 + \(\frac{1}{4}\)x
Answer:
The above-given equation:
1/2 x + 3 – 1/4 x = 3 + 1/4 x
subtract 3 from both sides
1/2x + 3 – 1/4 x -3 = 3 + 1/4x – 3
1/2 x – 1/4 x = 1/4 x
Find the least common multiple of 2, 4
The LCM is 4.
multiply by 4
1/2 x . 4 – 1/4 x . 4 = 1/4 x . 4
After simplification we get
2x – x = x
x = x
Now subtract x from both sides
x – x = x – x
0 = 0
Both sides are equal
Hence, it is true for all values of x.
Therefore, it has infinite solutions.

Question 8.
4 + 3x = 3x – 7
Answer:
The above-given equation:
4 + 3x = 3x – 7
Subtract 3x from both sides
4 + 3x – 3x = 3x – 7 – 3x
4 = -7
The sides are not equal.
Therefore, it has no solution.

Question 9.
5.4x + 12 = 2(2.7x – 9)
Answer:
The above-given equation:
5.4x + 12 = 2(2.7x – 9)
Expand: 2(2.7x – 9)
Apply the distributive law: a(b – c) = ab – ac
a = 2; b = 2.7x; c = 9
2. 2.7x – 2 . 9
multiply the numbers
5.4x – 18
5.4x + 12 = 5.4x – 18
subtract 12 from both sides
5.4x + 12 – 12 = 5.4x – 18 – 12
5.4x = 5.4x – 30
subtract 5.4x from both sides
5.4x – 5.4x = 5.4x – 30 – 5.4x
0 = -30
Tje sides are not equal
Hence, it has no solution.

Question 10.
6 + 2.5x = 0.5x – 8
Answer:
The above-given equation:
6 + 2.5x = 0.5x – 8
Multiply both sides by 10
6 . 10 + 2.5x . 10 = 0.5x . 10 – 8 . 10
60 + 25x = 5x – 80
subtract 60 from both sides
60 + 25x – 60 = 5x – 80 – 60
25x = 5x – 140
25x – 5x = -140
20x = -140
x = -140/20
x = -7
It has one solution.

Question 11.
2(x – 1) + 6x = 4(2x – 1) + 2
Answer:
The above-given equation:
2(x – 1) + 6x = 4(2x – 1) + 2
2x – 2 + 6x = 8x – 4 + 2
8x – 2 = 8x – 2
add 2 to the both sides
8x – 2 + 2 = 8x – 2 + 2
8x = 8x
subtract 8x to the both sides
8x – 8x = 8x – 8x
0 = 0
both sides are equal.
Hence, true for all values of x.

Question 12.
Carlos draws a square with side lengths 2x. Vincent draws a rectangle with a length of 2x + 4 and a width of 2x. Vincent says that he can choose a value for x so that the two shapes have the same perimeter. Carlos says this cannot be done. Who is correct and why?

Answer:
perimeter of a rectangle, P = 2 ( a+b) units
p =2(2x + 4 + 2x)
P = 2(4x + 4)
P = 8x + 8
perimeter of square = 4xside
P(S) = 4 x (2x)
P(S) = 8x
If we substitute x = 2
P(R) = 8(2) + 8
P(R) = 16 + 8
P(R) = 24
P(S) = 8(2)
P(S) = 16
Hence, Carlos is correct.
Because their perimetres are different.

Question 13.
Open-Ended Write an equation that has infinitely many solutions. Prove that your equation is correct.
Answer:
The number of solutions to an equation depends on the total number of variables contained in it. Thus, the system of the equation has two or more equations containing two or more variables.
To solve systems of an equation in two or three variables, first, we need to determine whether the equation is dependent, independent, consistent, or inconsistent. If a pair of the linear equations have unique or infinite solutions, then the system of equations is said to be a consistent pair of linear equations. Thus, suppose we have two equations in two variables as follows:
a₁x + b₁y = c₁ ——- (1)
a₂x + b₂y = c₂ ——- (2)
The given equations are consistent and dependent and have infinitely many solutions, if and only if,
(a₁/a₂) = (b₁/b₂) = (c₁/c₂)
The equation would be:
y = x + 3
y = 4; x = 1
4 = 1 + 3
4 = 4
both sides are equal
Hence, it has infinite solutions.

Question 14.
Molly charges an hourly fee to watch a pet plus an initial fee of $12. Bennett charges an hourly fee, but no initial fee. Can Molly and Bennett make the same amount? Write and solve an equation to justify your answer.


Answer:

For Problems 15-18, determine whether the equation has one solution, no solution, or infinitely many solutions.

Question 15.
\(\frac{1}{4}\)x + 7 + \(\frac{1}{4}\)x = 4 + \(\frac{5}{10}\)x + 3 _______________
Answer:
The above-given equation:
1/4 x + 7 + 1/4 x = 4 + 5/10 x + 3
Simplification:
Group-like terms:
1/4 x + 1/4 x + 7 = 4 + 5/10x + 3
add like terms:
2/4 x + 7 = 7 + 5/10 x
1/2 x + 7 = 7 + 1/2 x
subtract 1/2 x from both sides
1/2 x + 7 – 1/2 x = 7 + 1/2 x – 1/2 x
7 = 7
both sides are equal.
Hence, it is true for all values of x.
Therefore, it has infinite solutions.

Question 16.
5(4 + x) = x + 44 _______________
Answer:
The above-given equation:
5(4 + x) = x + 44
expand: 5(4 + x)
use distributive law
20 + 5x = x + 44
5x – x = 44 – 20
4x = 24
x = 24/4
x = 6
Therefore, it has only one solution.

Question 17.
0.25 + 2x = 2x – 1.75 _______________
Answer:
The above-given equation:
0.25 + 2x = 2x – 1.75
subtract 2x from both sides
0.25 + 2x – 2x = 2x – 1.75 – 2x
0.25 = -1.75
both sides are not equal.
Hence, it has no solution.

Question 18.
3x + 1 = 6x – 8 _______________
Answer:
The above-given equation:
3x + 1 = 6x – 8
subtract 1 from both sides
3x + 1 – 1 = 6x – 8 – 1
3x = 6x – 9
subtract 6x from both sides
3x – 6x = 6x – 9 – 6x
-3x = -9
x = 3
Therefore, it has unique solution.

I’m in a Learning Mindset!

What did I learn from writing an equation with infinitely many solutions that I can use in my future learning?

Lesson 3.2 More Practice/Homework

Examine Special Cases

Question 1.
Denis orders a large pizza for $16.50 plus $2 for each topping. Sheng orders a medium pizza for $13.25 plus $2 for each topping. Can they both pay the same total amount if they get the same number of toppings? Write an equation and explain.
Answer:
The total amount for large pizza = 16.50 + 2 = $18.5
The total amount for medium pizza = 13.25 + 2 = $15.25

Question 2.
Health and Fitness Shara scored 34 points in the basketball game last night. She scored six 3-point baskets and the rest were 2-point baskets. Write an equation to determine how many 2-point baskets Shara scored. Determine how many solutions the equation has.

Answer:
The total number of points = 34
The number of 3-point baskets = 6
The number of 2-point baskets = x
The equation wold be:
6(3) + 2(x) = 34
18 + 2x = 34
2x = 34 – 18
2x = 16
x = 16/2
x = 8

Question 3.
Construct Arguments Blake says that 4(x – 1) = 12 – 4x has zero solutions. Is Blake correct? Explain why or why not.
Answer:
Blake is wrong. The equation will get a unique solution.
Explanation:
The above-given equation:
4(x – 1) = 12 – 4x
Simplification:
4x – 4 = 12 – 4x
add 4 to both sides
4x – 4 + 4 = 12 – 4x + 4
4x = 16 – 4x
4x + 4x = 16
8x = 16
x = 16/8
x = 2
Therefore, it has an unique solution.

Complete each equation so that it has one solution.

Question 4.
-2(z + 3) – z = ___ – 4(z + 2)
Answer:
If we substitute the numbers in the place of blank then we get one solution.
For example, we substituted 8.
-2(z + 3) – z = 8 – 4(z + 2)
Simplification:
-2z – 6 – z = 8 – 4z – 8
-3z – 6 = -4z
-6 = -4z + 3z
-6 = -z
‘-‘ gets cancelled on both sides and we get
z = 6.
Therefore, it has one solution.

Question 5.
\(\frac{1}{4}\)x – 4(2) = –\(\frac{1}{2}\)(\(\frac{1}{2}\)x + ___)
Answer:
The above-given equation:
1/4 x – 4(2) = -1/2 x + ….
If we substitute the number ‘1’ then the equation would be:
1/4 x – 8 = -1/2 x + 1
add 8 to both sides
1/4 x – 8 + 8 = -1/2 x + 1 + 8
1/4 x = -1/2 x + 9
add 1/2 x to the both sides
1/4 x + 1/2 x = -1/2 x + 9 + 1/2 x
3/4 x = 9
Multiply both sides by 4
4 . 3/4 x = 9 . 4
3x = 36
x = 12
Hence, it has one solution.

Complete each equation so that it has infinitely many solutions.

Question 6.
\(\frac{3}{4}\) + x = 2x – x + ___
Answer:
The above-given equation:
3/4 + x = 2x – x + …
Here we substituted ‘3/4’
3/4 + x = 2x – x + 3/4
Simplification:
subtract 3/4 from both sides
3/4 + x – 3/4 = 2x – x + 3/4 – 3/4
x = 2x – x
x = x
if we subtract x from both sides
x – x = x – x
0 = 0
both sides are equal
Hence, it is true for all values of x.
Therefore, it has infinite solutions.

Question 7.
2h – 3(3 – h) + ___ = 5b – 8
Answer:

Complete each equation so that it has no solution.

Question 8.
6x + 5 = 3 + ___
Answer:
The above-given equation:
6x + 5 = 3 + ….
Let the blank be 6x then the equation is:
6x + 5 = 3 + 6x
Simplification:
subtract 6x from both sides
6x + 5 – 6x = 3 + 6x – 6x
5 = 3
both sides are not equal
Hence, it has no solution.

Question 9.
-k + ___ (k + 1) = 2k
Answer:
The above-given equation:
-k + ___ (k + 1) = 2k
If we substitute the 3 then the equation would be:
-k + 3 (k + 1) = 2k
-k + 3k + 3 = 2k
2k + 3 =2k
subtract 3 from both sides
2k + 3 – 3 = 2k – 3
2k = 2k – 3
subtract 2k from both sides
2k – 2k = 2k – 3 -2k
0 = -3
both sides are not equal
Hence, there is no solution.

For Problems 10-12, determine whether each equation has one solution, no solution,, or infinitely many solutions. If there is only one solution, find it.

Question 10.
Math on the Spot
A. x + 8x + 4 = 9x + 4
_______________
Answer:
The above-given equation:
x + 8x + 4 = 9x + 4
Simplification:
Subtract 4 from both sides
x + 8x + 4 – 4 = 9x + 4 – 4
If we simplify this, we get
x + 8x = 9x
add similar elements
9x = 9x
if we subtract 9x from both sides
9x – 9x = 9x -9x
0 = 0
both sides are equal
true for all x
Hence, it has infinite solutions.

B. 4(y + 5) = y – 10 + 3y
_______________
Answer:
The above-given equation:
4(y + 5) = y – 10 + 3y
Steps:
Group like terms:
4(y + 5) = y + 3y – 10
add similar elements
4(y+ 5) = 4y – 10
Expand 4(y + 5) = 4y +20
4y + 20 = 4y – 10
subtract 20 from both sides
4y + 20 – 20 = 4y – 10 -20
if we simplify this, we get
4y = 4y -30
subtract 4y from both sides
4y – 4y = 4y – 30 – 4y
0 = -30
The sides are not equal
Hence, no solution.

Question 11.
3.2(x – 1) = 2.2x + 1
Answer:
Steps:
Multiply both sides by 10
3.2(x – 1) . 10 = 2.2x . 10 + 1 . 10
after simplification
32(x – 1) = 22x + 10
32x – 32 = 22x + 10
add 32 to the both sides
32x – 32 + 32 = 22x + 10 + 32
add like terms:
32x = 22x + 42
subtract 22x from both sides
32x – 22x = 22x + 42 – 22x
10x = 42
x = 42/10
x = 21/5
Hence, it has only one solution.

Question 12.
3m – 2 = 25 – 6m
Answer:
The above-given equation:
3m – 2 = 25 – 6m
add 2 to both sides
3m – 2 + 2 = 25 – 6m + 2
3m = 27 – 6m
add 6m to the both sides
3m + 6m = 27 – 6m + 6m
9m = 27
m = 27/9
m = 3
hence, it has one solution.

Test Prep

Question 13.
What missing value would make the equation have infinitely many solutions?
2(3 + 4x) = 8x +
A. 1.5
B. 3
C. 6
D. 6x
Answer: Option C is correct.
Go for option verification.
or once observe the equation and see which option is suitable.
I will go for option C
The above-given equation:
2(3 + 4x) = 8x + …
We substituted the number 6.
2(3 + 4x) = 8x + 6
Simplification:
6 + 8x = 8x + 6
subtract 6 from both sides
6 + 8x – 6 = 8x + 6 – 6
8x = 8x
sides are equal
Hence, it is true for all values of x.
Therefore, it has infinite solutions.

Question 14.
How many solutions does the following equation have? If there is only one solution, find it.
3 + \(\frac{4}{5}\)x = \(\frac{9}{10}\)x
Answer:
The above-given equation:
3 + 4/5 x = 9/10 x
Simplification:
subtract 3 from both sides
3 + 4/5 x – 3 = 9/10 x – 3
4/5 x = 9/10 x – 3
subtract 9/10 x from both sides
4/5 x – 9/10 x = 9/10 x – 3 – 9/10 x
-1/10 x = -3
multiply both sides by -10
(-1/10 x)  (-10) = (-3) (-10)
x = 30
Hence, it has one solution.

Question 15.
Complete the equation so that it has no solution. 10.5x – 4 = 5 +
Answer:
The above-given equation:
10.5x – 4 = 5 + …
Let the empty box be 10.5x
10.5x – 4 = 5 + 10.5x
subtract 10.5x from both sides
10.5x – 4 – 10.5x = 5 + 10.5x – 10.5x
-4 = 5
the sides are not equal
Hence, there is no solution.

Question 16.
Complete the equation so that it has the solution c = 4.
5(2c – ) = 2(c + 11)
Answer:
The above-given equation:
5(2c – …) = 2(c + 11)
If we substitute the value 2 then the equation will be
5(2c – 2) = 2(c +11)
10c – 10 = 2c + 22
10c – 2c = 22 + 10
8c = 32
c = 32/8
c = 4
Therefore, the answer is 2.

Question 17.
How many solutions does the following equation have? If there is only one solution, find it.
2x + 8 = 2(x + 3)
A. one solution; x = -5
B. one solution; x = 5
C. no solution
D. infinitely many solutions
Answer: Option C is correct.
The given equation:
2x + 8 = 2(x + 3)
Now substitute the ‘x’ value.
here we are going for option verification.
First check for option A.
x = -5
2(-5) + 8 = 2(-5 + 3)
-10 + 8 = 2(-2)
-2 = -4
The sides are not equal.

Spiral Review

Question 18.
Complete each figure so it is congruent to the figure shown.

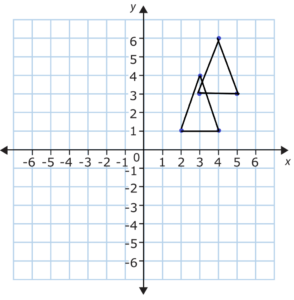
Answer:

Question 19.
The coordinates of the vertices of the preimage of a triangle are (2, 1), (3, 4), and (4, 1). The coordinates of the vertices of the image are (3, 3), (4, 6), and (5, 3). How far and in what direction was the triangle translated?
Answer: