We included HMH Into Math Grade 7 Answer Key PDF Module 8 Lesson 3 Apply Two-Step Inequalities to Solve Problems to make students experts in learning maths.
HMH Into Math Grade 7 Module 8 Lesson 3 Answer Key Apply Two-Step Inequalities to Solve Problems
I Can write and solve two-step inequalities for real-world scenarios.
Step It Out
Question 1.
A population study was performed to find the number of deer in two parks. The study found that twice the number of deer in Maple Park is at least 20 more than the number of deer in Smith Park. The study found that there are 50 deer in Smith Park.

A. Write an expression to represent the difference between twice the number of deer in Maple Park and the number of deer in Smith Park. Use x for the number of deer in Maple Park.
Answer:
2x – 50
Explanation:
Twice the number of deer in Maple Park is at least 20 more than the number of deer in Smith Park
2x – 50
the difference between twice the number of deer in Maple Park and the number of deer in Smith Park
2x- 50
B. What do you know is true about this difference?
The difference is ___________ than or equal to __________.
Answer:
The difference is greater than or equal to 20
C. Write and solve the inequality to determine the possible number of deer in Maple Park.
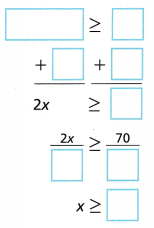
Answer:
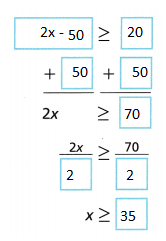
D. Graph the solution of the inequality. Do all the values make sense? Explain.

Answer:
Yes, all the values make sense.
Explanation:

only whole numbers can make sense.
E. What does the solution of the inequality represent in the problem?
In __________ Park, there are ____________ deer.
Answer:
In Maple Park, there are at least 35 deer.
Explanation:

Question 2.
Rosina and Asia collect stamps. The number of stamps Rosina has is 7 more than 3 times the number of stamps Asia has. Rosina has less than 85 stamps. How many stamps can Asia have?

A. Asia has x stamps. Write an expression to represent how many stamps Rosina has.
Answer:
3x + 7
Explanation:
The number of stamps Rosina has is 7 more than 3 times the number of stamps Asia has.
3x + 7
B. What do you know about the number of stamps Rosina has in her collection?
Rosina has (less / more) than ___________ stamps
Answer:
Rosina has less than 85 stamps
Explanation:
The number of stamps Rosina has is 7 more than 3 times the number of stamps Asia has.
Rosina has less than 85 stamps
C. Write and solve an inequality to find the number of stamps Asia has in her collection.
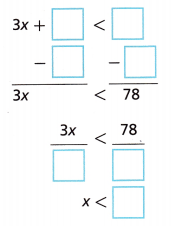
Answer:
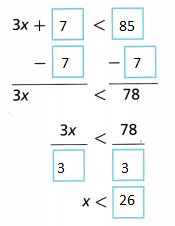
D. Graph the solution of the inequality. Do all the values make sense? Explain.
![]()
Answer:
Yes, the values make sense.
![]()
Explanation:
In the given graph solution 26 is a whole number.
E. What does the solution of the inequality represent in the problem?
The number of stamps that Asia has is (less / greater) than ___________.
Answer:
The number of stamps that Asia has is less than 26.
Explanation:

Question 3.
Solve the inequality: -3b – 2 ≤ 13.
A. -3b – 2 ≤ 13
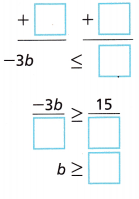
Answer:
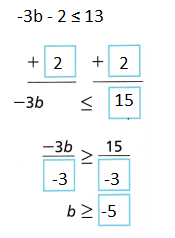
B. Graph the solution of the inequality.
Answer:
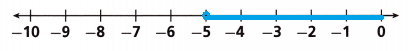
Explanation:
The numbers on number line are negative integers.
Turn and Talk Is -5 a solution of the inequality in Problem 3? Explain.
Answer:
Yes, the inequality: -3b – 2 ≤ 13.
Explanation:
the inequality: -3b – 2 ≤ 13.
greater then equal to -5
b ≥ -5
Question 4.
Monica and Lucy are participating in a scavenger hunt. The number of items Monica found is 7 more than j the number of items Lucy found. The number of items Monica found is at least 17.
A. Lucy found x items. Write an expression to represent how many items Monica found. Then complete the sentence about the number of items
___________ The number of items Monica found is (less / greater) than or equal to __________.
Answer:
\(\frac{1}{2}\)x + 7 The number of items Monica found is greater than or equal to17.
B. Write and solve the inequality to find what you know about the number of items Lucy found.
\(\frac{1}{2}\)x + 7 ≥ 17
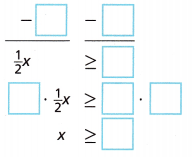
Answer:
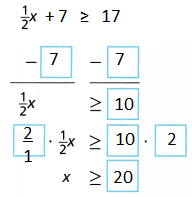
C. Graph the solution. Do all the values make sense? Explain.

Answer:
Yes, all the values make sense.
Explanation:

only whole numbers make sense.
The number 20 on number lines make sense.
D. What does the solution of the inequality mean in the problem?
Lucy found (less/greater than) or equal to ________ items.
Answer:
Lucy found greater than or equal to 20 items.
Explanation:
Check Understanding
Question 1.
Solve the inequality – 7m + 4 < -45. Graph the solution.

Answer:
m < 7

Explanation:
– 7m + 4 < -45
– 7m < -45 -4
7m < 49
m < 7
Question 2.
The number of students using the cafeteria’s healthy lunch line can be found by solving the inequality \(\frac{1}{2}\)s – 51 ≤ 20. How many students use this lunch line?
Answer:
s ≤ 142
Explanation:
\(\frac{1}{2}\)s – 51 ≤ 20
\(\frac{1}{2}\)s ≤ 20 +51
\(\frac{1}{2}\)s ≤ 71
s ≤ 71 x 2
s ≤ 142
On Your Own
Question 3.
Attend to Precision A warehouse has 2,100 tables packaged in boxes. The daily shipment is shown. After how many days will there be fewer than 1,500 tables in the warehouse?

![]()
A. Write and solve an inequality for this situation.
Answer:
x < 24

Explanation:
2100 – 25x < 1500
– 25x < 1500 – 2100
– 25x < – 600
25x < 600
x < 600/25
x < 24
B. Graph the solution of the inequality.
![]()
Answer:

Explanation:
The whole numbers on number line make a sense.
C. Do all the values make sense? What does the solution of the inequality represent in this context?
Answer:
No
Explanation:
only whole numbers less then 24 make a sense.
Question 4.
Attend to Precision Zachary and Dovante deliver packages. Dovante delivers 9 less than 4 times the number of packages Zachary delivers in one day. Dovante delivers no more than 11 packages in one day.
A. Write and solve an inequality to find the number of packages Zachary delivers in one day. Graph the solution of the inequality.
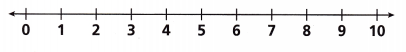
Answer:
x > 5
Explanation:

4x – 9 > 11
4x > 11 + 9
4x > 20
x > 20 /4
x > 5
B. Do all the values make sense? What does the solution of the inequality represent in this context?
Answer:
Yes, all the values make sense.
Explanation:
The numbers on number line are whole numbers and make sense.
For Problems 5-8, solve the inequality. Graph the solution.
Question 5.
6x – 11 > 67

Answer:
x > 13

Explanation:
6x – 11 > 67
6x > 67 + 11
6x > 78
x > 78/6
x > 13
Question 6.
3w + 1 ≥ 19
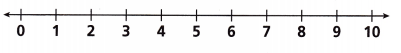
Answer:
w ≥ 6

Explanation:
3w + 1 ≥ 19
3w ≥ 19 -1
3w ≥ 18
w ≥ 18/3
w ≥ 6
Question 7.
-13d + 6 ≤ 45
![]()
Answer:
d ≤ -3

Explanation:
-13d + 6 ≤ 45
-13d ≤ 45 – 6
-13d ≤ 39
d ≤ – 39/13
d ≤ -3
Question 8.
-8n – 4 < -60
![]()
Answer:
n < 7

Explanation:
-8n – 4 < -60
-8n < -60 + 4
-8n < -56
n < 56/8
n < 7
Question 9.
Felipe is distributing discount coupons for a concert. He starts with 25 coupons. He gives 2 coupons to each person he sees. He will leave to get more coupons when he has fewer than 4 coupons left. How many people will Felipe give coupons to before he leaves to get more?
A. What is an inequality for this situation? What is the solution?
Answer:
25 – 2x < 4
B. What does the solution of the inequality mean in this context? Explain.
Answer:
10 people
Explanation:
25 – 2x < 4
-2x < 4 – 25
-2x < -21
x < 21/2
Question 10.
Attend to Precision Alicia is mixing paint. She has a bucket that contains 5\(\frac{1}{2}\) pints of paint. She adds \(\frac{1}{4}\)-pint containers of paint to the bucket until she has at most 8\(\frac{3}{4}\) pints of paint in the bucket. How many containers of paint can she add to the bucket?

Answer:
24 containers
Explanation:
5\(\frac{1}{2}\) + \(\frac{1}{4}\)x < 8\(\frac{3}{4}\)
\(\frac{1}{4}\)x < 8\(\frac{3}{4}\) – 5\(\frac{1}{2}\)
\(\frac{1}{4}\)x < \(\frac{35}{4}\)– \(\frac{11}{2}\)
\(\frac{1}{4}\)x < \(\frac{35}{4}\)– \(\frac{22}{4}\)
\(\frac{1}{4}\)x < \(\frac{35 – 11}{4}\)
\(\frac{1}{4}\)x < \(\frac{24}{4}\)
x < \(\frac{24}{4}\) \(\frac{4}{1}\)
x < 24
Question 11.
Open-Ended Write a two-step inequality whose solution is represented by the number line.
![]()
Answer:
d ≤ -2
Explanation:
-6d + 6 ≤ 18
-6d ≤ 12
d ≤ – 12/6
d ≤ -2
For Problems 12-17, solve the inequality. Graph the solution.
Question 12.
\(\frac{2}{3}\)t – \(\frac{1}{6}\) ≤ \(\frac{5}{6}\)

Answer:
t ≤ \(\frac{3}{2}\)

Explanation:
\(\frac{2}{3}\)t – \(\frac{1}{6}\) ≤ \(\frac{5}{6}\)
\(\frac{2}{3}\)t ≤ \(\frac{5}{6}\) + \(\frac{1}{6}\)
\(\frac{2}{3}\)t ≤ \(\frac{5 + 1}{6}\)
\(\frac{2}{3}\)t ≤ \(\frac{6}{6}\)
t ≤ \(\frac{6}{6}\) x\(\frac{3}{2}\)
t ≤ \(\frac{3}{2}\)
Question 13.
–\(\frac{3}{4}\)m + \(\frac{1}{4}\) ≥ 4\(\frac{3}{4}\)
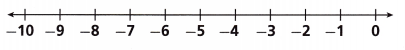
Answer:
m ≥ -6

Explanation:
–\(\frac{3}{4}\)m + \(\frac{1}{4}\) ≥ 4\(\frac{3}{4}\)
–\(\frac{3}{4}\)m ≥ 4\(\frac{3}{4}\) – \(\frac{1}{4}\)
–\(\frac{3}{4}\)m ≥ 4\(\frac{3}{4}\) – \(\frac{1}{4}\)
–\(\frac{3}{4}\)m ≥ \(\frac{193}{4}\) – \(\frac{1}{4}\)
–\(\frac{3}{4}\)m ≥ \(\frac{19 – 1}{4}\)
–\(\frac{3}{4}\)m ≥ \(\frac{18}{4}\)
\(\frac{3}{4}\)m ≥ – \(\frac{18}{4}\)
m ≥ – \(\frac{18}{4}\) \(\frac{4}{3}\)
m ≥ -6
Question 14.
–\(\frac{1}{10}\)a – \(\frac{2}{5}\) > \(\frac{3}{10}\)
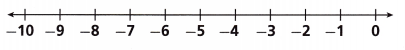
Answer:
a >-7
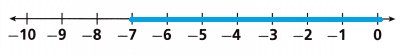
Explanation:
–\(\frac{1}{10}\)a – \(\frac{2}{5}\) > \(\frac{3}{10}\)
–\(\frac{1}{10}\)a > \(\frac{3}{10}\) + \(\frac{2}{5}\)
–\(\frac{1}{10}\)a > \(\frac{3}{10}\) + \(\frac{4}{10}\)
–\(\frac{1}{10}\)a > \(\frac{7}{10}\)
a >- \(\frac{7}{10}\) –\(\frac{10}{1}\)
a >-7
Question 15.
\(\frac{3}{8}\)w + 5 < 11
![]()
Answer:
w < -16

Explanation:
\(\frac{3}{8}\)w + 5 < 11
\(\frac{3}{8}\)w < 11 – 5
\(\frac{3}{8}\)w < -6
w < -6 \(\frac{8}{3}\)
W < – 2 x 8
w < -16
Question 16.
\(\frac{1}{2}\)r + 5 ≤ 17
![]()
Answer:
r ≤ 24

Explanation:
\(\frac{1}{2}\)r + 5 ≤ 17
\(\frac{1}{2}\)r ≤ 17 -5
\(\frac{1}{2}\)r ≤ 12
r ≤ 12 \(\frac{2}{1}\)
r ≤ 24
Question 17.
2\(\frac{2}{3}\)b + 8 ≥ 0
![]()
Answer:
b ≥ -6

Explanation:
2\(\frac{2}{3}\)b + 8 ≥ 0
2\(\frac{2}{3}\)b ≥ -8
\(\frac{2}{3}\)b ≥ -4
b ≥ -4\(\frac{3}{2}\)
b ≥ -6
Question 18.
Financial Literacy Ariana started a savings account with $240. She deposits $30 into her account at the end of each month. She wants to know how many months it will take for her account to have a balance greater than $500.
A. Model with Mathematics Write and solve an inequality that represents this situation.
Answer:
9 months
Explanation:
Financial Literacy Ariana started a savings account with $240.
She deposits $30 into her account at the end of each month.
She wants to know how many months it will take for her account to have a balance greater than $500.
240 + 30x > 500
30x > 500 – 240
30x > 260
x > 260 /30
x > 8.66 or 9 months
B. Reason How many months will ¡t take for her account to have a balance greater than $500? Explain.
Answer:
9 months
Explanation:
30x > 500 – 240
30x > 260
x > 260 /30
x > 8.66
For Problems 19-22, solve the inequality. Graph the solution.
Question 19.
-5y + 47 > -13

Answer:
y > 12

Explanation:
-5y + 47 > -13
-5y > -13 – 47
-5y > -60
5y > 60
y > 60/5
y > 12
Question 20.
18 – 4z ≥ 26
![]()
Answer:
z ≥ -2

Explanation:
18 – 4z ≥ 26
– 4z ≥ 26 – 18
– 4z ≥ 8
z ≥ -8/4
z ≥ -2
Question 21.
8g + 30 < -2
![]()
Answer:
g < – 4

Explanation:
8g + 30 < -2
8g < -2 – 30
8g < -32
g < -32/8
g < – 4
Question 22.
-7s – 4 ≤ 10
![]()
Answer:
s ≤ -2

Explanation:
-7s – 4 ≤ 10
-7s ≤ 10 + 4
-7s ≤ 14
s ≤ – 14/7
s ≤ -2
Question 23.
Colleen is attending a carnival. The price of admission into the carnival is shown. It costs $3 to play a game. Colleen has $35. What is the greatest number of games she can play?

Answer:
9 games
Explanation:
The price of admission into the carnival $3 to play a game.
Colleen has $35.
the greatest number of games she can play
8 + 3x < 35
3x < 35 – 8
3x < 27
x < 27/3
x < 9
Question 24.
A gift shop at an amusement park sells key chains. The gift shop has 55 key chains. When the number of key chains is below 10, the manager will reorder. If the gift shop sells 4 key chains each day, how many days will it take before the manager has to reorder?
Answer:
d > 11 days
Explanation:
The gift shop has 55 key chains.
When the number of key chains is below 10, the manager will reorder.
If the gift shop sells 4 key chains each day,
Number of days will it take before the manager has to reorder
4d + 10 > 55
4d > 55 – 10
4d > 45
d > 45/4 =11.25
Lesson 8.3 More Practice/Homework
Solve the inequality. Graph the solution.
Question 1.
5x + 13 ≤ 48

Answer:
x ≤ 7

Explanation:
5x + 13 ≤ 48
5x ≤ 48 – 13
5x ≤ 35
x ≤ 7
Question 2.
16 – 7v < 2

Answer:
v < 2

Explanation:
16 – 7v < 2
– 7v < 2 -16
– 7v < -14
7v < 14
v < 14/7
v < 2
Question 3.
9r – \(\frac{3}{5}\) > 3\(\frac{9}{10}\)

Answer:
r > \(\frac{1}{2}\)

Explanation:
9r – \(\frac{3}{5}\) > 3\(\frac{9}{10}\)
9r > 3\(\frac{9}{10}\) + \(\frac{3}{5}\)
9r > \(\frac{39}{10}\) + \(\frac{6}{10}\)
9r > \(\frac{45}{10}\)
r > \(\frac{45}{9 x 10}\)
r > \(\frac{5}{10}\)
r > \(\frac{1}{2}\)
Question 4.
-8c + 13 ≥ 47
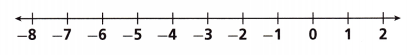
Answer:
c > -4.25

Explanation:
-8c + 13 ≥ 47
-8c ≥ 47 – 13
-8c ≥ 34
c ≥ -34/8
c ≥ -4.25
Question 5.
Math on the Spot Members of the drama club plan to present its annual spring musical. They have $1,262.50 left from fundraising, but they estimate that the entire production will cost $1,600.00. How many tickets at the price shown must they sell to at least break even?

Answer:
x ≥ 50
Explanation:
Members of the drama club have $1,262.50 left from fundraising, but they estimate that the entire production will cost $1,600.00.
Number of tickets at the price shown must they sell to at least break even
1262.50 + 6.75x ≥ 1600.00
6.75x ≥ 1600.00 – 1262.50
6.75x ≥ 337.5
x ≥ 337.5/6.75
x ≥ 50
Question 6.
Model with Mathematics Jenna has a collection of trading cards. She started her collection with 175 cards. She buys packs of cards that contain 15 cards each. Solve an inequality to determine how many packs of cards Jenna buys so that she will have over 400 cards in her collection.
A. What is an inequality that represents this situation? What is the solution?
Answer:
15c + 175 ≥ 400
Explanation:
Jenna has started her collection with 175 cards.
She buys packs of cards that contain 15 cards each.
Total packs of cards Jenna buys so that she will have over 400 cards in her collection.
15c + 175 ≥ 400
B. How many packs of cards does Jenna buy?
Answer:
15 packs of cards
Explanation:
Jenna has started her collection with 175 cards.
She buys packs of cards that contain 15 cards each.
Total packs of cards Jenna buys so that she will have over 400 cards in her collection.
15c + 175 ≥ 400
15c ≥ 400 – 175
15c ≥ 225
c ≥ 225/15
c ≥ 15
Question 7.
Model with Mathematics Drew and Larry are working together on a jigsaw puzzle. Drew places 11 less than 3 times the number of pieces that Larry places. Drew places at least 10 pieces. How many pieces does Larry place?
Answer:
7 pieces
Explanation:
Drew places 11 less than 3 times the number of pieces that Larry places.
Drew places at least 10 pieces.
Total pieces does Larry place
3m – 11 ≥ 10
3m ≥ 10 +11
3m ≥ 21
m ≥ 21/3
m ≥ 7
Test Prep
Question 8.
Dwight and Wait are building model cars. Dwight builds 7 fewer models than 4 times the number Walt builds. Dwight builds at most 9 models. Which inequality could be used to find the number of models Walt builds?
(A) 4m – 7 < 9
(B) 4m – 7 ≤ 9
(C) 4m – 7 > 9
(D) 4m – 7 ≥ 9
Answer:
Option (B)
Explanation:
Dwight builds 7 fewer models than 4 times the number Walt builds.
4m – 7
Dwight builds at most 9 models
≤ 9
inequality could be used to find the number of models Walt builds
4m – 7 ≤ 9
Question 9.
A truck rental company rents a truck for a one-time fee of $25 plus $1.50 per mile traveled. Kelly has $80 she can spend on the rental truck. What is the greatest number of miles that she can travel?
Answer:
x > 37
Explanation:
A truck rental company rents a truck for a one-time fee of $25 plus $1.50 per mile traveled.
Kelly has $80 she can spend on the rental truck.
the greatest number of miles that she can travel,
1.5x + 25 > 80
1.5x > 80 – 25
1.5x > 55
x > 55/1.5
x > 36.66
Question 10.
Ricardo measured the temperature in the morning. The temperature was -6 °C. The temperature is increasing 1\(\frac{1}{2}\) °C every hour. After how many hours will the temperature be at least 2 °C? Select the best answer.
(A) less than 1\(\frac{1}{3}\) hours
(B) more than 2\(\frac{1}{3}\) hours
(C) less than 4 hours
(D) 5\(\frac{1}{3}\) hours or more
Answer:
Option(D)
Explanation:
The temperature was -6 °C.
The temperature is increasing 1\(\frac{1}{2}\) °C every hour.
After how many hours will the temperature be at least 2 °C
-6 + 1\(\frac{1}{2}\)t ≥ 2
1\(\frac{1}{2}\)t ≥ 2 + 6
\(\frac{3}{2}\)t ≥ 8
t ≥ 8 x \(\frac{2}{3}\)
t ≥ \(\frac{16}{3}\)
5\(\frac{1}{3}\) hours or more
Spiral Review
Question 11.
A football team earns 6 points for a touchdown and 3 points for a field goal. In one game, a team scored a touchdown and some field goals. The total points the team scored is 18 points. Write an equation that can be used to find the number of field goals the team scored.
Answer:
6 + 3p
Explanation:
A football team earns 6 points for a touchdown and 3 points for a field goal.
The total points the team scored is 18 points.
The number of field goals the team scored,
6 + 3p =18
3p = 12
p = 3
Question 12.
Scott makes and sells bracelets. He spends $28 on supplies, and he sells each bracelet for $6. Write an expression that represents his profit for selling b bracelets.
Answer:
6b – 28 > 28
Explanation:
6b – 28 > 28
spends $28 on supplies
he sells each bracelet for $6
an expression that represents his profit for selling b bracelets.
6b > 28+28
b > 56/6 = 9.33 = 10 bracelets