We included HMH Into Math Grade 7 Answer Key PDF Module 7 Lesson 4 Apply Two-Step Equations to Solve Real-World Problems to make students experts in learning maths.
HMH Into Math Grade 7 Module 7 Lesson 4 Answer Key Apply Two-Step Equations to Solve Real-World Problems
I Can use two-step equations to solve a variety of problems.
Spark Your Learning
A diagram of the rectangular sitting area in a botanical garden is shown. What is the length of the sitting area in the garden?

Answer:
Length of the sitting area in the garden = 20 ft
Explanation:
Given width =10 ft
Perimeter = 60 ft
The perimeter of a rectangular garden = 2 (l + b)
60 ft = 2(l + 10)
60 ft ÷ 2 = (l + 10)
30ft = l + 10
l = 30 – 10
l = 20 ft
Turn and Talk How else could you have represented the situation with the garden?
Build Understanding
Question 1.
Lucy scored 20 points in her basketball game. She made 4 of her free throws, worth 1 point each, and made no 3-point field goals. How many 2-point field goals did she make?
Answer:
Lucy scored 20 points
Ans she made 4 of her free throws.
4 × 1 = 4
20 – 4 = 16
16 ÷ 2 = 8
Lucy made 2-point field goals.
Connect to Vocabulary
A solution of an equation is the value we can put in place of a variable(such as x) that makes the equation true.
A. Write an equation to represent this situation.
Answer:
2x – 4 = 20
B. Model the equation with algebra tiles.
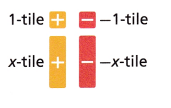
Answer:
1 tile + 1 tile = x tile + x tile
C. How can you work with the algebra tiles on the equation mat so one side of the mat has only variables?
Answer:
x + x tile = 40
D. How can you now use the tiles to find the value of the variable?
Answer:
1 tile + 1 tile = x tile + x tile
2 tile = 2x tile
E. What is the solution of the equation and the solution to the problem?
Answer:
2x – 4 = 20
2x = 24
x = 24 ÷ 2
x = 12
F. What was the sequence of math operations used in this model?
Answer:
G. Jerry solved the equation 2x – 4 = 20 by adding four 1-tiles to each side. Explain why Jerrys method works.
Answer:
Given equation 2x – 4 = 20
By adding 4 1-tiles on each side
2x – 4 + 4 = 20 + 4
2x = 24
x = 24 ÷ 2
x = 12
Turn and Talk How are solving 2x + 4 = 20 and 2x – 4 = 20 alike? How are they different?
Answer:
The given equations are different because we can find the value of x.
Given equation is 2x + 4 = 20 and 2x – 4 = 20
2x + 4 = 20
2x – 4 = 20
4x = 40
x = 20
Step It Out
Question 2.
Mr. Maxwell bought new basketball shoes with the discount shown. He has a $10-off coupon he can use after the percentage discount. If Mr. Maxwell bought the shoes for $61.25, what was the original price?

A. If the shoes are discounted 25%, what percent of the original price is the discounted price?
25% discount is the same as ![]() % of the original price.
% of the original price.
Answer:
25% discount is the same as 75% of the original price.
B. Fill in the boxes to set up the equation to find the original price of the shoes.
![]() % • Original Price –
% • Original Price – ![]() = 61.25
= 61.25
Answer:
25% Original price – 10 = 61.25
C. What would be the price without a $10-off coupon?
61.25 + ![]() =
= ![]() $ ____________
$ ____________
Answer:
61.25 + 10 = $71.25.
D. Complete the equation that can be solved to find the price of the shoes before the 25% off discount.
![]() • Original Price =
• Original Price = ![]()
Answer:
Orginal Price = $95.
E. Find the original price of the shoes.
Original Price = 71.25 ÷ ![]()
The original price was $__________.
Answer:
The original price was $95.
Explanation:
Original Price = 71.25 ÷ 0.75
= $95.
F. Solve the equation from Step B algebraically. Then solve the problem.
Let x represent the original price of the shoes.
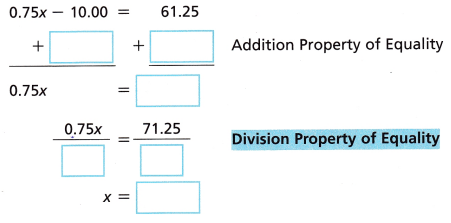
The original price of the shoes was $ _____________.
Answer:
The original price of the shoe was $95.
Explanation:

Turn and Talk Compare the arithmetic solution from Parts C, D, and E to the algebraic solution in Part F.
Answer:
The arithmetic solution from Parts C, D, and E to the algebraic solution in Part F are all asked to find the original price.
Question 3.
Tracy’s fitness goal for this week is shown on her planner. To meet her goal, she will need a total of 8 pushups more than her current daily total of morning and evening pushups. Tracy has been doing 25 pushups in the evening. How many pushups has she been doing in the morning?

A. Write and solve an equation to find her current number of morning pushups.
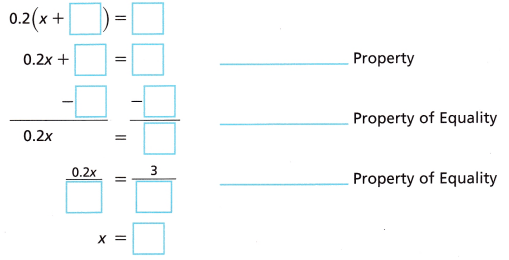
Answer:
Her current number of morning pushups is 15.
B. Check your solution.
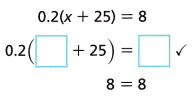
Answer:
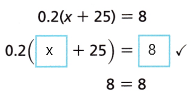
Check Understanding
Question 1.
Cookie Castle sells 8-inch cookies for $3 plus a flat $5 delivery fee. Zach has $14 to spend on cookies. Write and solve an equation to determine how many cookies Zach can buy and have delivered.
Answer:
Zach can buy 3 cookies.
Explanation:
Cookies for $3
A flat delivery fee $5.
Zach spent on cookies = $14
$14 – $5 = x × $3
$9 = $3x
x = $9
Question 2.
A kitten is born having a mass of 90 grams and gains 10 grams per day. How many days will it take the kitten to double its mass? Write and solve the equation.
Answer:
9 days.
Explanation:
Mass = 90 grams and Gain = 10 grams per day.
180 = 90 + 10x
10x = 180 – 90
10x = 90
x = 90 ÷ 10
x = 9
Question 3.
Mr. Muñoz has a coupon for 15% off his entire purchase. He buys binoculars for $105 and hiking boots. He spends a total of $170 before tax. Write and solve an equation to find how much the hiking boots cost before the discount.
Answer:
x = 154.25
Explanation:
Mr. Munoz has a coupon for 15% off his entire purchase.
He bought binoculars and hiking boots for $105.
He spends a total of $170 before tax.
Let us assume the hiking boots cost as x.
So the equation is
105(0.15) + x =170
15.75 + x = 170
x = 170 – 15.75
x = 154.25
The hiking boots cost before the discount is 154.25.
On Your Own
Question 4.
The formula F = 1.8C + 32 can be used to convert temperature units. F is degrees Fahrenheit, and C is degrees Celsius. Convert the December record low temperature to Celsius. Round to the nearest tenth.

Answer:
Given,
F = 1.8C + 32
December -5 °F
1.8 × c + 32 = -5
1.8 c = -5 – 32
1.8 c = -38
c = -38 ÷ 1.8
c = 21.11 °C.
The December record low temperature to Celsiud is 21 °C
Question 5.
Dirk sold 7 more than 2 times as many gym memberships this month than last month. This month he sold 43 memberships.
A. Use arithmetic to find the number of memberships Dirk sold last month.
Answer:
He sold 43 memberships
43 – 7 = 36
36 ÷ 2 = 18
B. Use algebra to find the number of memberships Dirk sold last month.
Answer:
The number of memberships Dirk sold last month is 18.
Explanation:
Dirk sold x memberships last month
2x + 7 = 43
2x = 43 – 7
2x = 36
x = 36 ÷ 2
x = 18
C. Compare the sequence of math operations in Part A and Part B.
Answer:
The sequence of math operations in Part A and Part B are same.
Question 6.
Model with Mathematics Arlene buys a phone case and charging cord for 15% off. The original cost of the phone case is $18. Her total discount is $4.20. Write and solve an equation to find the original price of the charging cord.
Answer:
x = 10
Explanation:
Based on the given conditions
calculate 15% × (18 + x) = $4.20
2.7 + 0.15x = 4.2
0.15x = 4.2 – 2.7
0.15x = 1.5
x = 1.5 ÷ 0.15
x = 10
The original price of the charging cord is $10.
Question 7.
Model with Mathematics Taka is playing a game of darts. She scores 52 points. In the game she is playing, she gets a -3 score each time she misses the board. Her final point total is 37. Write and solve an equation to find out how many times she missed the board.
Answer:
52 – 3x = 37
Explanation:
An equation to find out how many times she missed the board is 52 – 3x = 37
52 – 37 = 3x
15 = 3x
3x = 15
x = 15 ÷ 3
x = 5
For Problems 8-15, solve each equation. Check your solution.
Question 8.
-9d – 1 = 17
Answer:
d = -2
Explanation:
Given,
-9d – 1 = 17
-9d = 17 + 1
-9d = 18
-d = 18 ÷ 9
d = -2
Question 9.
2 + \(\frac{1}{6}\)a = -4
Answer:
a = 36
Explanation:
Given,
2 + \(\frac{1}{6}\)a = -4
2 + 4 = \(\frac{1}{6}\)a
6 = \(\frac{1}{6}\)a
a = 6 × 6
a = 36
Question 10.
24 = 3(w + 5)
Answer:
w = 3
Explanation:
Given,
24 = 3(w + 5)
24 = 3w + 15
24 – 15 = 3w
3w = 9
w = 9 ÷ 3
w = 3
Question 11.
–\(\frac{4}{5}\)(f + 5) = -12
Answer:
f = 40
Explanation:
Given,
–\(\frac{4}{5}\)(f + 5) = -12
–\(\frac{4}{5}\) f – 5 × –\(\frac{4}{5}\) = -12
–\(\frac{4}{5}\) f + (5 × 4) = -12
–\(\frac{4}{5}\) f + 20 = -12
–\(\frac{4}{5}\) f = -12 -20
–\(\frac{4}{5}\) f = -32
-f = (-32 × 5) ÷ 4
-f = -160 ÷ 4
f = 40
Question 12.
\(\frac{g}{3}\) – 7 = 15
Answer:
g = 66
Explanation:
Given,
\(\frac{g}{3}\) – 7 = 15
\(\frac{g}{3}\) = 15 + 7
\(\frac{g}{3}\) = 22
g = 22 × 3
g = 66
Question 13.
-3 + \(\frac{p}{7}\) = -5
Answer:
p = -14
Explanation:
Given,
-3 + \(\frac{p}{7}\) = -5
\(\frac{p}{7}\) = -5 + 3
\(\frac{p}{7}\) = -2
p = -2 × 7
p = -14
Question 14.
-17 + \(\frac{b}{8}\) = 13
Answer:
b = 160
Explanation:
Given,
-17 + \(\frac{b}{8}\) = 13
\(\frac{b}{8}\) = 13 + 17
\(\frac{b}{8}\) = 20
b = 20 × 8
b = 160
Question 15.
\(\frac{k}{2}\) + 9 = 30
Answer:
k = 42
Explanation:
Given,
\(\frac{k}{2}\) + 9 = 30
\(\frac{k}{2}\) = 30 – 9
\(\frac{k}{2}\) = 21
k = 21 × 2
k = 42
Question 16.
Model with Mathematics Mr. Burns takes a one-day trip and rents a car using the rates shown. The car rental cost is $68.25. Write and solve an equation to find how many miles he traveled.

Answer:
He traveled 475 miles.
Explanation:
Given the car rental cost = $68.25
Rates $0.07 per mile
The equation is
0.07m + 35 = $68.25
0.07m = 68.25 – 35
0.07m = 33.25
m = 33.25 ÷ 0.07
m =475 miles
Question 17.
Model with Mathematics Geoff works at a warehouse, earning $17.50 per hour plus a $200 one-time hiring bonus. In Geoff’s first week, his pay including the bonus was $637.50. Write and solve an equation to find how many hours Geoff worked his first week.
Answer:
Geoff worked 25 hours in his first week.
Explanation:
Subtract $200 from $637.50
$637.50 – $200 = $437.50
Then divide $437.50 by $17.50
= 25
That means Geoff worked 25 hours in his first week.
Question 18.
Attend to Precision A regular hexagon has sides of length x + 5 and a perimeter of 72 inches. Write and solve an equation to find x. How long is a side?
Answer:
x = 7
Explanation:
6 (x + 5) = 72
6x + 30 = 72
6x = 72 – 30
6x = 42
x = 42 ÷ 6
x = 7
For Problems 19-26, solve each equation. Check your solution.
Question 19.
-3(n + 5) = 12
Answer:
n = 1
Explanation:
Given,
-3(n + 5) = 12
-3n – 15 = 12
-3n = 12 – 15
-3n = -3
n = 1
Question 20.
7(c – 12) = -21
Answer:
c =9
Explanation:
Given,
7(c – 12) = -21
7c – 84 = -21
7c = -21 + 84
7c = 63
c = 63 ÷ 7
c =9
Question 21.
-9h – 15 = 93
Answer:
h = 12
Explanation:
Given,
-9h – 15 = 93
-9h = 93 + 15
-9h = 108
h = 108 ÷ 9
h = 12
Question 22.
\(\frac{z}{5}\) + 3 = -35
Answer:
z = -190
Explanation:
Given,
\(\frac{z}{5}\) + 3 = -35
\(\frac{z}{5}\) = -35 – 3
\(\frac{z}{5}\) = -38
z = -38 × 5
z = -190
Question 23.
\(\frac{3}{8}\)n + 1 = -25
Answer:
n = 69.33
Explanation:
Given,
\(\frac{3}{8}\)n + 1 = -25
\(\frac{3}{8}\)n = -25 – 1
\(\frac{3}{8}\)n = -26
n = -26 × \(\frac{8}{3}\)
n = -208 ÷ 3
n = 69.33
Question 24.
2x – 5 = 15
Answer:
x = 10
Explanation:
Given,
2x – 5 = 15
2x = 15 + 5
2x = 20
x = 20 ÷ 2
x = 10
Question 25.
3(y + \(\frac{2}{5}\)) = –\(\frac{1}{5}\)
Answer:
y = \(\frac{7}{15}\)
Explanation:
Given,
3(y + \(\frac{2}{5}\)) = –\(\frac{1}{5}\)
3y + 3 × \(\frac{2}{5}\) = –\(\frac{1}{5}\)
3y + \(\frac{6}{5}\) = –\(\frac{1}{5}\)
3y = –\(\frac{1}{5}\) – \(\frac{6}{5}\)
3y = \(\frac{7}{5}\)
y = \(\frac{7}{15}\)
Question 26.
2(p + 14) = 0
Answer:
p = 14
Explanation:
Given,
2(p + 14) = 0
2p + 28 = 0
2p = -28
p = 28 ÷ 2
p = 14
Question 27.
Open-Ended Write a word problem that is represented by the equation 3x + 15 = 42.
Answer:
The product of a number and three-plus fifteen is equal to 42.
I’m in a Learning Mindset!
How do I keep myself motivated to solve problems with twa-step equations?
Lesson 7.4 More Practice/Homework
Question 1.
Model with Mathematics Julie wants to buy tulip bulbs to plant. Each bulb costs $0.50 plus a one-time $4.50 shipping cost. She has $22 to spend. Write and solve an equation to determine how many bulbs Julie can buy and have shipped.
Answer:
x = 35
Explanation:
Based on the given question calculate
4.5 + 0.5 × x = 22
4.5 + 0.5x = 22
0.5x = 22 – 4.5
0.5x = 17.5
x = 17.5 ÷ 0.5
x = 35
Question 2.
Math on the Spot The total charge for a yearly Internet movie rental membership is $231. A registration fee of $15 is paid up front, and the rest is paid monthly. How much do new members pay each month?
Answer:
new members pay a fee of $18 per month.
Explanation:
Total rental membership = $231
Registration fee = $15
Fee after registration =$231 -$15
= $216
New members pay each month = $216 ÷ 12
= 18
new members pay a fee of $18 per month.
Question 3.
Attend to Precision Beverly is making peanut butter-banana bread. She always doubles the amount of nuts and peanut butter chips. The total amount of chips and nuts after doubling is 4\(\frac{1}{2}\) cups. Write and solve an equation to find the original amount of nuts in the recipe.

Answer:
x = 3
Explanation:
Total amount = amount of chips + amount of nuts
x + 1\(\frac{1}{2}\) = 4\(\frac{1}{2}\)
x = 4\(\frac{1}{2}\) – 1\(\frac{1}{2}\)
x = \(\frac{9}{2}\) – \(\frac{3}{2}\)
x = \(\frac{6}{2}\)
x = 3
For Problems 4-7, solve each equation. Check your solution.
Question 4.
3 = 0.2m – 7
Answer:
m = 50
Explanation:
Given
3 = 0.2m -7
3 + 7 = 0.2m
10 = 0.2m
m = 10 ÷ 0.2
m = 50
Question 5.
1.3z + 1.5 = 5.4
Answer:
z = 3.9
Explanation:
Given
1.3z + 1.5 = 5.4
1.3z = 5.4 – 1.5
1.3z = 3.9
z = 3.9 ÷ 1.3
z = 3
Question 6.
-3(t + 6) = 0
Answer:
t = -6
Explanation:
Given,
-3(t + 6) = 0
-3t – 18 = 0
-3t = 18
-t = 18 ÷ 3
-t = 6
t = -6
Question 7.
-8(1 – g) = 56
Answer:
g = 8
Explanation:
Given,
-8(1 – g) = 56
-8 + 8g = 56
8g = 56 + 8
8g = 64
g = 64 ÷ 8
g = 8
Question 8.
Open-Ended Write a two-step equation that involves multiplication and subtraction, includes a negative coefficient, and has a solution of x = 7.
Answer:
-2x – 7 = -21
Explanation:
x = 7
-2x – 7 = -21
-2x = -21 + 7
-2x = -14
x = 14 ÷ 2
x = 7
Question 9.
Open-Ended Write a two-step equation that involves division and addition and has a solution of x = -25.
Answer:
2x – 25 = -75
Explanation:
Let us consider a variable x.
First add both side of the by 25
2x = -75 + 25
2x = -50
Next step is divide both side of the equation by 2.
x = -50 ÷ 2
x = -25
Test Prep
Question 10.
Leo started working for a new company that paid him $25 per hour with a hiring bonus of $100. During the first two weeks he was paid $1,200, which included the bonus. How many hours did he work during the first two weeks?
(A) 40
(B) 44
(C) 48
(D) 52
Answer:
44 hours.
Explanation:
Given,
The money paid by company = $25 per hour
Hiring bonus = $100
Total money paid = $1200
let the number of hours of work be n
Total money paid for first two weeks = $100 + $25 × n
$1200 = $100 + $25 × n
$1200 – $100 = $25n
$200 = $25 × n
n = $200 ÷ 25
n = 44 hours
Question 11.
To convert to degrees Fahrenheit, use the formula F = \(\frac{9}{5}\)C + 32, where C is the degrees in Celsius. From the choices below, which is the first step to solve for Celsius if the temperature is 70 °F?
(A) Add 32 to both sides.
(B) Subtract 32 from both sides.
(C) Divide both sides by \(\frac{5}{9}\).
(D) Multiply both sides by \(\frac{9}{4}\).
Answer:
Divide both sides by \(\frac{5}{9}\).
Explanation:
F = \(\frac{9}{5}\)C + 32
If F = 85, then
85 = \(\frac{9}{5}\)C + 32
85 – 32 = \(\frac{9}{5}\)C
53 = \(\frac{9}{5}\)C
c = 53 × \(\frac{5}{9}\)
Question 12.
Fred earns $16.50 an hour for overtime. He worked overtime on Monday and Thursday this week. On Monday, he worked 4 hours of overtime. His total overtime pay for the week was $123.75. Write and solve an equation to find the number of overtime hours Fred worked on Thursday.
Answer:
x = 26.93 = 26\(\frac{15}{16}\)
Explanation:
Based on the given question
calculate = 4 × (4 + x ) = 123.75
= 16 + 4x = 123.75
4x = 123.75 – 16
4x = 107.75
x = 107. 75 ÷ 4
x = 26.93
Question 13.
Solve \(\frac{1}{2}\)m – 5 = 23.
(A) 13.5
(B) 27
(C) 33
(D) 56
Answer:
m = 36
Explanation:
Given equation \(\frac{1}{2}\)m – 5 = 23.
Now let us solve the given equation
\(\frac{m}{2}\) -5 = 23
m – 10 = 23 × 2
m – 10 = 46
m = 46 – 10
m = 36
Spiral Review
Question 14.
Apples at the farmers’ market cost $2.50 for 5 apples or $0.70 for 1 apple. Which is the better buy if you want 5 apples? Explain.
Answer:
$2.50
Explanation:
apples cost $2.50 for 5 apples
1 apple cost $0.70.
If you multiply 0.70 by $5 it is 3.5$ which is more expensive.
Therefore $2.50 is the better deal.
Question 15.
Mr. Spencer drives 200 miles in 5 hours. What is his unit rate?
Answer:
40 miles per hour
Explanation:
Distance = 200 miles
time = 5 hours
Speed = distance ÷ time
= 200 ÷ 5
= 40 miles per hour.