We included HMH Into Math Grade 7 Answer Key PDF Module 3 Review to make students experts in learning maths.
HMH Into Math Grade 7 Module 3 Review Answer Key
Vocabulary
Select all terms that apply to each number.
Question 1.

Answer:
23 is a positive integer.
There is no negative sign so the number 23 is not a negative integer.
23 is not a perfect square so it is not a rational number.

Question 2.

Answer:
-3/10 is a negative integer
-3/10 is a rational number. All rational numbers are able to be written as a fraction or ratio of two integers.

Question 3.

Answer:
1.4 is a positive integer.
1.4 is not a negative integer and not a rational number.

Question 4.

Answer:
-7 is a negative integer
-7 is a rational number because it can be written in fraction form.

Concepts and Skills
Question 5.
Use Tools Name two numbers that are 7 units from 3. State what strategy and tool you will use to answer the question, explain your choice, and then find the answer.
Answer:
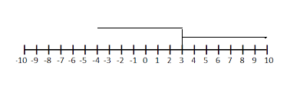
Two numbers: -4 and 10
Question 6.
A school, a bookstore, and a park are on the same straight street. The book store (6) is 2.25 miles from the school (S). The park (P) is 1.75 miles from the school. What is the distance from the park to the bookstore?

_____ miles
Answer:
Given,
A school, a bookstore, and a park are on the same straight street.
The book store (6) is 2.25 miles from the school (S).
The park (P) is 1.75 miles from the school.
To find:
What is the distance from the park to the bookstore?
2.25 – 1.75 = 0.50 miles
So, the distance from the park to the bookstore is 0.5 miles.
Question 7.
Paolo is using number lines to find the value of the expression \(\frac{1}{6}\) + \(\frac{2}{3}\) + (-1\(\frac{1}{3}\)). His first two steps are shown.
A. Draw an arrow on the number line provided to show the last step.
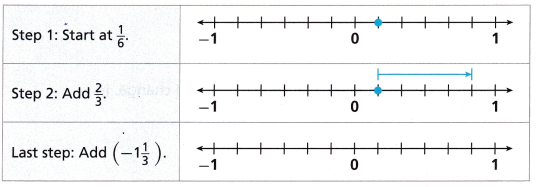
Answer:
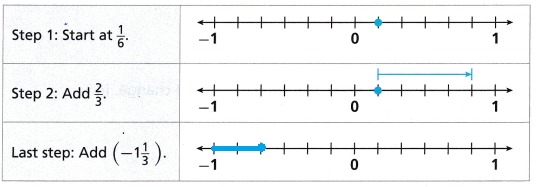
B. What is the value of the expression \(\frac{1}{6}\) + \(\frac{2}{3}\) + (-1\(\frac{1}{3}\))? __________
Answer:
\(\frac{1}{6}\) + \(\frac{2}{3}\) + (-1\(\frac{1}{3}\))
\(\frac{1}{6}\) + \(\frac{2}{3}\) – 1\(\frac{1}{3}\)
LCD of 6 and 3 is 6.
\(\frac{1}{6}\) + \(\frac{2}{3}\) – \(\frac{4}{3}\)
\(\frac{1}{6}\) + \(\frac{4}{3}\) – \(\frac{8}{6}\)
(1+4-8)/6 = -3/6 = -1/2
Question 8.
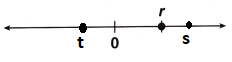
A number line is shown. Eric knows that n is the opposite of m. Which statement about m and n is true?
![]()
A. m = n
B. m = -(-n)
C. m + n = 0
D. m – n = 0
Answer:
n is located on the negative part and m is located on the positive part.
Opposite of -n is m.
m + n = 0
m = -n
Option C is the correct answer.
Question 9.
The difference a – b is equal to c. The number line shows a and b. Select all statements about c that are true.
A c < 0
B. c = 0
C. c > 0
D. c is closer to 0 on the number line than a.
E. c is the same distance from 0 on the number line as a.
F. c is farther from 0 on the number line than a.
Answer:
C. c > 0
E. c is the same distance from 0 on the number line as a.
Question 10.
On a quiz show, Anabel started with 0 points. She gained 10 points on her first turn and lost 10 points on her second turn. What is her combined score after her first two turns? Use addition of integers to explain your reasoning.
Answer:
10 + (-10) = 10 – 10 = 0
The combined score after her first two turns is 0.
Question 11.
An equation is shown, where s > 0 and t < 0.
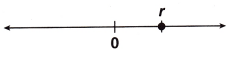
Plot and label two points on the number line to show possible locations of s and t.
Answer:
Question 12.
Ivy’s hair has grown \(\frac{5}{8}\) inch since her last haircut. At this haircut, she has 1\(\frac{1}{2}\) inches of hair cut off.
A. Which expressions represent the total change, in inches, in the length of Ivy’s hair between her two most recent haircuts?
A. \(\frac{5}{8}\) – 1\(\frac{1}{2}\)
Answer:
\(\frac{5}{8}\) – 1\(\frac{1}{2}\)
Rewriting the equation
\(\frac{5}{8}\) – 1 – \(\frac{1}{2}\)
\(\frac{5}{8}\) – \(\frac{1}{2}\)
LCD of 8 and 2 is 8.
\(\frac{5}{8}\) – \(\frac{4}{8}\) = \(\frac{1}{8}\)
-1 + \(\frac{1}{8}\) = –\(\frac{7}{8}\)
B. \(\frac{5}{8}\) + (-1\(\frac{1}{2}\))
Answer:
\(\frac{5}{8}\) + (-1\(\frac{1}{2}\))
+ × – = –
\(\frac{5}{8}\) – 1\(\frac{1}{2}\)
Rewriting the equation
\(\frac{5}{8}\) – 1 – \(\frac{1}{2}\)
\(\frac{5}{8}\) – \(\frac{1}{2}\)
LCD of 8 and 2 is 8.
\(\frac{5}{8}\) – \(\frac{4}{8}\) = \(\frac{1}{8}\)
-1 + \(\frac{1}{8}\) = –\(\frac{7}{8}\)
C. \(\frac{5}{8}\) + 1\(\frac{1}{2}\)
Answer:
Rewriting the equation
\(\frac{5}{8}\) + 1 + \(\frac{1}{2}\)
\(\frac{5}{8}\) + \(\frac{1}{2}\)
LCD of 8 and 2 is 8.
\(\frac{5}{8}\) + \(\frac{4}{8}\) = \(\frac{9}{8}\)
1 + 1 + \(\frac{1}{8}\) = 2\(\frac{1}{8}\)
D. -1\(\frac{1}{2}\) – \(\frac{5}{8}\)
Answer:
-1\(\frac{1}{2}\) – \(\frac{5}{8}\)
-(1\(\frac{1}{2}\) + \(\frac{5}{8}\))
Rewriting the equation
-(\(\frac{5}{8}\) + 1 + \(\frac{1}{2}\))
-(latex]\frac{5}{8}[/latex] + \(\frac{1}{2}\))
LCD of 8 and 2 is 8.
-(\(\frac{5}{8}\) + \(\frac{4}{8}\)) = –\(\frac{9}{8}\)
-1 – 1 – \(\frac{1}{8}\) = -2\(\frac{1}{8}\)
E. 1\(\frac{1}{2}\) – \(\frac{5}{8}\)
Answer:
1\(\frac{1}{2}\) – \(\frac{5}{8}\)
1 + \(\frac{1}{2}\) – \(\frac{5}{8}\)
\(\frac{1}{2}\) – \(\frac{5}{8}\) = –\(\frac{1}{8}\)
1 – \(\frac{1}{8}\) = \(\frac{7}{8}\)
B. Plot a point on the number line to represent the total change, in inches, in the length of Ivy’s hair after both haircuts.
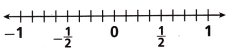
Answer: