Into Math Grade 7 Module 11 Answer Key Analyze Surface Area and Volume

We included HMH Into Math Grade 7 Answer Key PDF Module 11 Analyze Surface Area and Volume to make students experts in learning maths.

HMH Into Math Grade 7 Module 11 Answer Key Analyze Surface Area and Volume

The Prism Family

Each of the rectangular prisms shown is made from cubes with an edge length of 1 centimeter. All of the prisms in this family have something in common.

Investigate by finding the dimensions, surface area, and volume of each prism. How are they all related?
A.

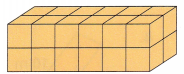
Dimensions: _____________, ___________, ___________
Surface area: _____________
Volume: _____________
Answer:
Dimensions: 2cm, 6cm, 2cm
Surface area: 56 cm²
Volume: 24 cm³
Explanation:
Dimensions: l = 2cm, w = 6cm, h = 2cm
Surface area: A
A = 2(l x w + w x h x h x l)
A = 2(6×2 + 2×2 + 2×6)
A = 2(12 + 4 + 12)
A = 2(28)
A = 56 cm²
Volume: V = (l).(w).(h)
V = 2 x 6 x 2 = 24 cm³

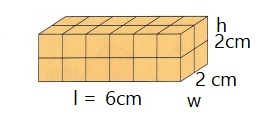
B.

Dimensions: _____________, ___________, ___________
Surface area: _____________
Volume: _____________
Answer:
Dimensions: 4cm, 2cm, 3cm
Surface area: 52 cm²
Volume: 24 cm³
Explanation:

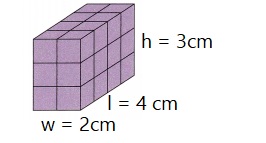
Dimensions: l = 4cm, w = 2cm, h = 3cm
Surface area: A
A = 2(l x w + w x h x h x l)
A = 2(4×2 + 2×3 + 3×4)
A = 2(8 + 6 + 12)
A = 2(26)
A = 52 cm²
Volume: V = (l).(w).(h)
V = 4 x 2 x 3 = 24 cm³

C.

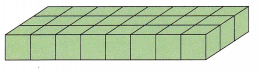
Dimensions: _____________, ___________, ___________
Surface area: _____________
Volume: _____________
Answer:
Dimensions: 8cm, 3cm, 1cm
Surface area: 70 cm²
Volume: 24 cm³
Explanation:

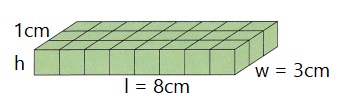
Dimensions: l = 8cm, w = 3cm, h = 1cm
Surface area: A
A = 2(l x w + w x h x h x l)
A = 2(8×3 + 3×1 + 1×8)
A = 2(24 + 3 + 8)
A = 2(35)
A = 70 cm²
Volume: V = (l).(w).(h)
V = 8 x 3 x 1 = 24 cm³

Turn and Talk

Describe the family of rectangular prisms.
Answer:
A rectangular prism is a three-dimensional shape, having six faces,
where all the faces (top, bottom, and lateral faces) of the prism are rectangles. Cuboids, Rectangular Prisms and Cubes.

Are You Ready?

Complete these problems to review prior concepts and skills you will need for this module.

Explore Volume

Each rectangular prism is composed of cubes with an edge length of 1 inch. Determine the volume of each prism.

Question 1.

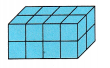
__________ in³
Answer:
16 cm³
Explanation:
Volume: V = (l).(w).(h)
V = 4 x 2 x 2 = 16 cm³

Question 2.

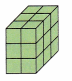
__________ in³
Answer:
18 cm³
Explanation:
Volume: V = (l).(w).(h)
V = 2 x 3 x 3 = 18 cm³

Nets and Surface Area

Draw a net of each prism. Then use the net to determine the surface area of the prism.

Question 3.

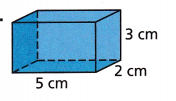
____________ cm²
Answer:
A = 62 cm²
Explanation:

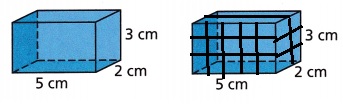
Dimensions: l = 5cm, w = 2cm, h = 3cm
Surface area: A
A = 2(l x w + w x h x h x l)
A = 2(5×2 + 3×2 + 3×5)
A = 2(10 + 6 + 15)
A = 2(31)
A = 62 cm²

Question 4.

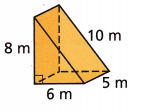
____________ m²
Answer:
A = 168 m²
Explanation:

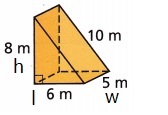
A = 2(l x w + w x h x h x l)
A = (6×5 + 5×8 +10×5) + 6×8
A = 30 + 40 + 50 + 48
A = 168 m²

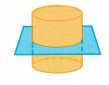
Cross Sections of Circular Solids

Question 5.

Answer:
There are two different types of the cross-section.
1. Horizontal or parallel cross-section.
2. Vertical or perpendicular cross-section.
Explanation:
Horizontal cross-section:
A plane cuts the solid shape in the horizontal direction(parallel to the base).

Vertical cross-section:
A plane cuts the solid shape in the vertical direction(perpendicular to the base).

Question 6.
Can a plane slice a cone so that the cross-section of the cone is a triangle? Explain.
Answer:
Yes, slice of cone is triangle.
Explanation:

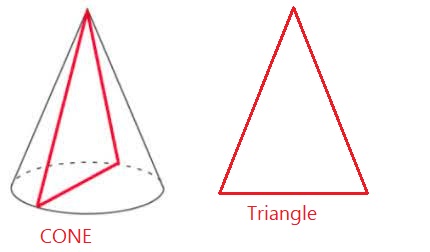
Vertical cross-section:
A plane cuts the solid shape in the vertical direction(perpendicular to the base).