Into Math Grade 6 Module 5 Lesson 4 Answer Key Find and Apply Unit Rates

We included HMH Into Math Grade 6 Answer Key PDF Module 5 Lesson 4 Find and Apply Unit Rates to make students experts in learning maths.

HMH Into Math Grade 6 Module 5 Lesson 4 Answer Key Find and Apply Unit Rates

I Can find and use unit rates to solve problems.

Step It Out

1. Jack is at the supermarket. He finds a 5-pound bag of flour and a 2-pound bag of flour priced as shown. Which of the two bags of flour is the better buy?

A. Write a rate to represent the cost per pound of the 5-pound bag of flour.

Answer:
The rate to represent the cost per pound of the 5-pound bag of flour is $2.69/5
B. Find the unit cost of the 5-pound bag of flour in dollars per pound. Round your answer to the nearest cent.

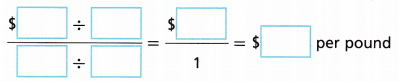
Answer:
5 = 2.69
1 = x
x = 2.69/5
x = $0.53 per pound
The unit cost of the 5-pound bag of flour in dollars per pound is $0.53
C. Find the unit cost of the 2-pound bag of flour in dollars per pound. Round your answer to the nearest cent.

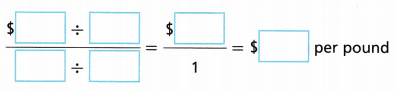
Answer:
1.89/2
1.89 = 2 pound
x = 1 pound
x × 2 = 1.89
x = 1.89/2
x = 0.945
0.945 per pound.
The unit cost of the 2-pound bag of flour in dollars per pound is $0.945
D. Which of the two bags of flour offers the better value? Explain.
______________________
______________________
______________________
Answer:
The unit cost of the 2-pound bag of flour in dollars per pound is $0.945
The unit cost of the 5-pound bag of flour in dollars per pound is $0.53
5-pound bag of flour offers a better value.

Turn and Talk Why is it helpful to use unit rates to compare prices? Explain.

2. It takes Kendra 27 minutes to run 3 miles.
A. Write a unit rate to represent Kendra’s running rate in minutes per mile.


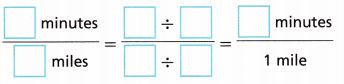
Answer:
It takes Kendra 27 minutes to run 3 miles.
27/3
27 = 3 miles
x = 1 mile
x × 3 = 27
x = 27/3
x = 9
It takes 9 minutes to run 1 mile.
Thus the unit rate to represent Kendra’s running rate in minutes per mile is 9 minutes per mile.
B. Write Kendra’s rate as a unit rate in miles per minute.

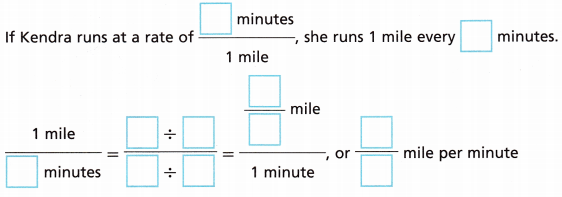
Answer:
27 = 3 miles
x = 1 mile
x × 3 = 27
x = 27/3
x = 9
It takes 9 minutes to run 1 mile.
Thus the unit rate to represent Kendra’s running rate in minutes per mile is 9 minutes per mile.
C. How many miles can Kendra run in 45 minutes?

Answer:
9 min = 1 mile
45 min = x mile
x × 9 = 45
x = 45/9
x = 5
Kendra run 5 miles in 45 minutes.

D. How many minutes would it take Kendra to run 7 miles?

Answer:
9 min = 1 mile
x = 7 mile
9 × 7 = x
x = 63 minutes
Thus Kendra took 63 minutes in 7 miles.

E. Compare the rates 9 minutes for 1 mile and 63 minutes for 7 miles. Are these rates equivalent? Why or why not?
9 minutes for 1 mile and 63 minutes for 7 miles are equivalent rates.

Turn and Talk Explain how you can find an equivalent rate given a unit rate. Give an example.

3. A potter takes a total of 7.5 hours to mold 12 clay pitchers.
A. Write the rate of the number of pitchers to the number of hours. Is it a unit rate? Explain.


Answer:
The rate of the number of pitchers to the number of hours = 12/7.5
B. Find the unit rate.

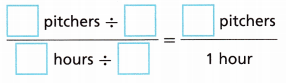
Answer:
12/7.5 = x/1
C. How many pitchers can the potter mold in 70 hours?

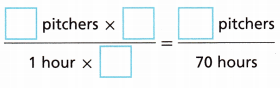
Answer:
12 pitcher × 1 = x × 7.5
x = 12 × 70 /7.5 = 112
x = 112 hours
D. How can you find how many hours it would take the potter to mold 60 pitchers?

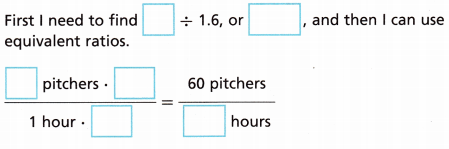
Answer:
(12 × 7.5) = 60 × x
90/60 = x
x = 1.5 hours

Check Understanding

Question 1.
A recipe for 12 servings of soup calls for 8 cups of chicken broth. How many cups of broth are needed to make 30 servings of the soup?
Answer:
Given,
A recipe for 12 servings of soup calls for 8 cups of chicken broth.
12/8 = 30/x
12 × x = 30 × 8
12x = 240
x = 240/12
x = 20
Thus 20 cups of broth are needed to make 30 servings of the soup.

Question 2.
A store sells two different-sized packages of AA batteries. Which package is the better buy? Explain.

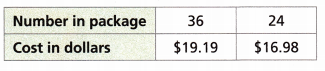
Answer:
The unit cost of 36 pack = 19.19/36 = 0.53
The unit cost of 24 pack = 16.98/24 = $0.71
The unit cost of 36 packs is less than 24 packs of AA batteries.
Therefore, 36 packs is a better buy.

On Your Own

Question 3.
STEM A Rube Goldberg machine consists of a series of devices that perform a simple task. Kate is drawing a scale model of her Rube Goldberg machine, which she plans to build and enter into a contest. A bicycle wheel on the scale model is 2 inches in diameter, while in the actual machine, it will be 28 inches in diameter.

A. Based on the measures of the wheel diameter, what is the unit rate of inches of machine per inch of the model?
______________________
Answer:
A bicycle wheel on the scale model is 2 inches in diameter, while in the actual machine, it will be 28 inches in diameter.
28/2 = 14
14 + 2 = 16
16 inches of machine per inch.

B. What would be the actual length of a rope that is 7.25 inches long in the model?
______________________
Answer:
16 + 7.25 = 23.25

Question 4.
Chen bought a 20-foot chain for $36.50.
A. What is the unit rate of price per foot? Round the unit rate to the nearest cent.
______________________
Answer:
36.50 ÷ 2 = 18.25

B. At this rate, what would be the price of a 30-foot chain?
______________________
Answer:
You would add 36.50 and 18.25 bc 18.25 is 10 feet

Question 5.
Reason A pool is being drained by a pump at a rate of 4 gallons per minute. An identical pump is added to help drain the pool. How does the second pump affect the rate of drainage? Explain.
______________________
Answer:

Question 6.
Melanie and her cousin Grace are arguing about who is the faster swimmer. The distance each can swim in a certain number of minutes is shown in the photo.

A. How fast does Melanie swim?
______________________
Answer:
Melanie swim 300m in 5 mins
300/5 = 60 m/ min

B. How fast does Grace swim?
______________________
Answer:
Grace swim 325m in 5.5 min
325/5.5 = 59.09

C. Who is the faster swimmer?
______________________
Answer:
Melanie swim 300m in 5 mins
300/5 = 60 m/ min
Grace swim 325m in 5.5 min
325/5.5 = 59.09
60 – 59.09 = 0.91
Melanie swim faster than grace.

Question 7.
Mr. Sen wants to treat a group of friends either to the movies or to a hockey game for his birthday. Both the theater and the hockey team offer group pricing, as shown in the table. Which offers the lesser price per person, the movies or the hockey game? Explain.

Answer:
Movie pricing = 54.25/7 = $7.75
Hockey game pricing = 94.8/12 = $7.9
Movie pricing offers a lesser price per person.

Question 8.
Jan takes 9 hours to paint 2 desk sets. At this rate, how long will it take her to paint 15 desk sets?
Answer:
Given,
Jan takes 9 hours to paint 2 desk sets
9 hours = 2 sets
x = 15 sets
x × 2 = 15 × 9
x = (15 × 9)/2
x = 67.5
Thus it will take 67 and half hours to paint 15 desk sets.

Question 9.
Cody’s aunt pays him $30 to walk her dog 6 times. At this rate, how many times must he walk the dog in order to earn $100?
Answer:
Given,
Cody’s aunt pays him $30 to walk her dog 6 times.
30 = 6
100 = x
x × 30 = 100 × 6
x × 3 = 60
x = 60/3
x = 20
Thus he walk 20 times in order to earn $100.

Question 10.
Jeff can read a 300-page book in 10 hours. His twin sister, Sasha, can read a 350-page book in 11 hours. Who reads at the faster rate?

Answer:
Jeff can read a 300-page book in 10 hours.
300 ÷ 10 = 30
His twin sister, Sasha, can read a 350-page book in 11 hours.
350 ÷ 11 = 31.8
By comparing both we can say that Jeff read faster than his sister.

Question 11.
Attend to Precision Ross has a model truck. It has a scale of 1 inch for every 32 inches on a real-sized truck. He wants to build a garage for the model at the same scale. Given that the garage for a real-sized truck is 12 feet wide, how wide should his model garage be?
Answer:
It has a scale of 1 inch for every 32 inches on a real-sized truck means the scale is 1:32
Put another way, the real-life width is 32 times greater than the scale model.
y = 32x
The garage in the real world is 12 feet wide, or 12×12 = 144 inches wide.
y = 144 into the equation and solve for x
y = 32x
32x = y
32x = 144
x = 144/32
x = 4.5
His scale model garage must be 4.5 inches wide.

Question 12.
Greg drove 300 miles at a constant speed in 5 hours. The speed limit was 70 miles per hour. Was his rate greater than the speed limit?
Answer:
Given,
Greg drove 300 miles at a constant speed in 5 hours.
The speed limit was 70 miles per hour.
To find the rate for how many miles Greg drove for 5 hours, we need to divide 300 by 5:
300/5 = 60
60 miles represents the speed for 1 hour.
60 is less than 70.
The inequality indicates that his rate is less than the speed limit.

Question 13.
Chris paddles 5 miles down a stream in 3 hours. How far will she have paddled in 9 hours at this rate?
Answer:
Given,
Chris paddles 5 miles down a stream in 3 hours
To find how far will she had paddled in 9 hours at this rate.
5 × 9 = x × 3
x = 45/3
x = 15

Question 14.
Jordan found cloth for $7.50 per yard. How much would his total cost be if he needed 12 yards of cloth?
Answer:
Given,
Jordan found cloth for $7.50 per yard.
he needed 12 yards of cloth.
7.50 × 12 = 90
The cost for 12 yards of cloth is $90.

Question 15.
Out of every 8 loaves of bread that Markelle bakes, 5 of them are pumpkin bread. At this rate, how many loaves of pumpkin bread would he have if he baked a total of 40 loaves of bread?
Answer:
Out of every 8 loaves of bread that Markelle bakes, 5 of them are pumpkin bread.
He baked a total of 40 loaves of bread.
(40 × 5)/8 = 5 × 5 = 25

Question 16.
Open Ended The table gives the costs of two different-sized cartons of eggs, one of which is pictured. Suppose a supermarket wants to sell eggs individually. Is there a price the supermarket can charge per egg that is between the prices per egg for the two different-sized cartons? Explain.

Answer:
The table gives the costs of two different-sized cartons of eggs, one of which is pictured. Suppose a supermarket wants to sell eggs individually.
The cost of 12 eggs = $3
Cost of 1 egg = x
x × 12 = 3
x = 3/12
x = $0.25
The cost of 18 eggs = $4.32
Cost of 1 egg = x
x × 18 = 4.32
x = 4.32/18
x = $0.24

For Problems 17-22, A) find each unit rate and B) use it to fill in the blank.

Question 17.
1 yard in 6 minutes
A. ____ B. ____ per 18 minutes
Answer:
1 yard in 6 minutes
1 yard = 6 minutes
x = 18 minutes
1 × 18 = x × 6
x = 18/6
x = 3
3 yard per 18 minutes

Question 18.
$72 for 7\(\frac{1}{2}\) hours
A. ____ B. ____ per 40 hours
Answer:
$72 for 7\(\frac{1}{2}\) hours
$72 = 7\(\frac{1}{2}\) hours
x = 40 hours
x × 7\(\frac{1}{2}\) = 40 × 72
x × 7\(\frac{1}{2}\) = 2880
x = 2880/7\(\frac{1}{2}\)
x = 384
So, $384 per 40 hours

Question 19.
$130.50 for 18 hours
A. ___ B. ___ per 40 hours
Answer:
$130.50 for 18 hours
130.5 = 18 hours
x = 40 hours
x × 18 = 130.5 × 40
x × 18 = 5220
x = 5220/18
x = 290
$290 per 40 hours

Question 20.
126 miles in 3\(\frac{1}{2}\) hours
A. ____ B. ____ per 9 hours
Answer:
126 miles in 3\(\frac{1}{2}\) hours
126 = 3\(\frac{1}{2}\) hours
x = 9 hours
x × 3\(\frac{1}{2}\) = 9 × 126
x × 3\(\frac{1}{2}\) = 1134
x = 1134/3.5
x = 324
324 miles per 9 hours.

Question 21.
2 inches in 5 seconds
A. ____ B. ____ per 15 seconds
Answer:
2 inches in 5 seconds
2 in = 5 sec
x = 15 sec
x × 5 = 2 × 15
x × 5 = 30
x = 30/5
x = 6
6 inches per 15 seconds.

Question 22.
$105 for 12\(\frac{1}{2}\) hours
A. ____ B. ____ per 40 hours
Answer:
$105 for 12\(\frac{1}{2}\) hours
105 = 12\(\frac{1}{2}\) hours
x = 40 hours
x × 12\(\frac{1}{2}\) = 105 × 40
x × 12.5 = 4200
x = 4200/12.5
x = 336
$336 per 40 hours.

Lesson 5.4 More Practice/Homework

Question 1.
Captain’s Lawn Service can mow 8 lawns in 5 hours. At this rate, how long does it take for the service to mow 12 lawns?
______________________
Answer:
Given,
Captain’s Lawn Service can mow 8 lawns in 5 hours.
We need to find out how long it takes for the service to mow 12 lawns.
(12 × 5)/8 = 15/2 = 7.5
It can be written as 7 1/2.

Question 2.
STEM Density is measured in units of mass per unit of volume. It can be thought of as a unit rate. The mass of a block of aluminum is 9.45 grams. The volume is 3.5 cubic centimeters (cm³). What is the density of the aluminum?
Answer:
Given that,
Density is measured in units of mass per unit of volume. It can be thought of as a unit rate.
The mass of a block of aluminum is 9.45 grams.
The volume is 3.5 cubic centimeters (cm³).
We know that,
Density = mass/volume
Mass = 9.45 g
Volume = 3.5 cu. cm
Density = 9.45/3.5 = 2.7 g/cm³

Question 3.
Math on the Spot A 3-pack of light bulbs costs $3.45. A 4-pack of the same light bulbs costs $4.20. Which pack is the better value?
Answer:
A 3-pack of light bulbs costs $3.45.
3.45 ÷ 3 = 1.15
A 4-pack of the same light bulbs costs $4.20
4.20 ÷ 4 = 1.05
Thus the 4 pack is a better value.

Question 4.
It takes Tyreke 28 minutes to bike to his school, which is 7 miles away. If Tyreke continues to pedal at this pace, how long would it take for him to get to the soccer field, which is 8.8 miles away from the school?

Answer:
Given,
It takes Tyreke 28 minutes to bike to his school, which is 7 miles away.
(28 × 8.8)/7
= 4 × 8.8
= 35.2

Question 5.
Attend to Precision Maria and Franco are draining water troughs on their farms. Maria’s trough drained 60 gallons of water 75 minutes. Franco’s trough drained 75 gallons of water in an hour and a half. Explain whose trough drained faster.
Answer:
Given,
Maria and Franco are draining water troughs on their farms.
Maria’s trough drained 60 gallons of water 75 minutes.
Franco’s trough drained 75 gallons of water in an hour and a half.
75/60 = 1.25 gallons per minute
90/75 = 1.2 gallons per minute
Thus Maria’s trough drained faster at 1.25 gallons a minute while Francos’ trough drained only 1.2 gallons per minute.

For Problems 6-9, A) find each unit rate and B) use it to find an equivalent rate.

Question 6.
3 feet in 4 minutes
A. ____ B. ____ per 16 minutes
Answer:
3 feet in 4 minutes
3 feet = 4 minutes
x = 16 minutes
x × 4 = 16 × 3
4x = 48
x = 48/4
x = 12
Thus 12 feet per 16 minutes.

Question 7.
473 heartbeats in 5\(\frac{1}{2}\) minutes
A. ____ B. ____ per 3 minutes
Answer:
473 heartbeats in 5\(\frac{1}{2}\) minutes
5 \(\frac{1}{2}\) minutes = 473
3 minutes = x
x × 5 \(\frac{1}{2}\) = 473 × 3
x × 5 \(\frac{1}{2}\) = 1419
x = 1419/5.5
x = 258
258 hearbeats per 3 minutes.

Question 8.
$12.00 for 48 cans
A. ___ B. ___ per 12 cans
Answer:
$12.00 for 48 cans
48 cans = $12
12 cans = x
x × 48 = 12 × 12
x × 48 = 144
x = 144/48
x = 3
$3 per 12 cans

Question 9.
$28.00 for 400 square feet
A. ___ B. ___ per 1,500 sq ft
Answer:
$28.00 for 400 square feet
400 sq. ft = $28
1500 sq. ft = x
x × 400 = 28 × 1500
x × 4 = 28 × 15
x = 7 × 15
x = 105
Thus $105 per 1500 sq. ft.

Test Prep

For Problems 10-11, use the following information.

A store sells two packages of the same brand of water bottles.

Question 10.
Which package has the better unit price per bottle?
Answer:
48 pack of 8 ounce bottles = $5.88
48 = $5.88
1 = x
x × 48 = 5.88
x = 5.88/48
x = 0.12
Thus the cost of 1 pack of 8 ounce bottles is $0.12
28 pack = 5.95
1 = x
x × 28 = 5.95
x = 5.95/28
x = 0.21
Thus the cost of 1 pack of 10 ounce bottles is $0.21
The cost of 8 ounce bottle has a better unit price.

Question 11.
Which package has the better unit price per ounce?
Answer: The package 10 ounce bottles have the better unit price per ounce,

Question 12.
Deanna will cook a turkey for about 15 minutes per pound of turkey. If she bought an 11-pound turkey, how long should she cook it?
Answer:
Given,
Deanna will cook a turkey for about 15 minutes per pound of turkey.
We have to find If she bought an 11-pound turkey, how long should she cook it.
Multiply 11 with 15
11 × 15 = 165 minutes
Thus Deanna cooks 165 minutes.

Question 13.
Orlo uses a spool of wire to make 15 necklaces. At this rate, how many spools of the same size would he use to make 50 necklaces?
Answer:
Given,
Orlo uses a spool of wire to make 15 necklaces.
To find At this rate, how many spools of the same size would he use to make 50 necklaces.
Based on the given conditions
50 ÷ 15 = 10/3
Thus he use 10/3 spools of the same size to make 50 necklaces.

Question 14.
Preston is buying 1-gallon cans of paint to paint a room. The information on the paint can says that a gallon of paint can cover 400 square feet. The room’s walls are 688 square feet combined. How many 1-gallon cans of paint does he need to buy to put 2 coats of paint on the walls?
A. 4 cans
B. 3 cans
C. 2 cans
D. 1 can
Answer:
Given,
Preston is buying 1-gallon cans of paint to paint a room.
The information on the paint can say that a gallon of paint can cover 400 square feet.
The room’s walls are 688 square feet combined.
688 × 2 = 1376
1376 ÷ 400 = 3.44 ≈ 4
Thus Option A is the correct answer.

Spiral Review

Question 15.
Juan bought 7.8 pounds of seedless red grapes for $2.85 per pound. How much did Juan spend on seedless red grapes?
Answer:
Given,
Juan bought 7.8 pounds of seedless red grapes for $2.85 per pound.
2.85 × 7.8 = 22.23
Thus Juan spends $22.23 on seedless red grapes.

Question 16.
Mrs. Kelly bought a bag of flour that holds 16\(\frac{2}{3}\) cups of flour. Each loaf of banana bread uses \(\frac{2}{3}\) cup of flour. How many loaves of banana bread can she make?
Answer:
Given,
Mrs. Kelly bought a bag of flour that holds 16\(\frac{2}{3}\) cups of flour.
Each loaf of banana bread uses \(\frac{2}{3}\) cup of flour.
16 \(\frac{2}{3}\) ÷ \(\frac{2}{3}\)
Convert from mixed fraction to the improper fraction
16 \(\frac{2}{3}\) = \(\frac{50}{3}\)
\(\frac{50}{3}\) ÷ \(\frac{2}{3}\)
\(\frac{50}{3}\) × \(\frac{3}{2}\) = 25
Thus she can make 25 loaves of banana bread.

Question 17.
The elevation at the top of a mountain is +150 feet. A reef’s elevation is -75 feet. Is the top of the mountain or the reef closer to sea level?
Answer: Reef’s elevation is closer to the sea level.