We included HMH Into Math Grade 6 Answer Key PDF Module 15 Measures of Center to make students experts in learning maths.
HMH Into Math Grade 6 Module 15 Answer Key Measures of Center
DOT PLOT LOGIC
The dot plot shows the lengths of eight hiking trails in a park.
- Use the dot plot and the clues to complete the table.
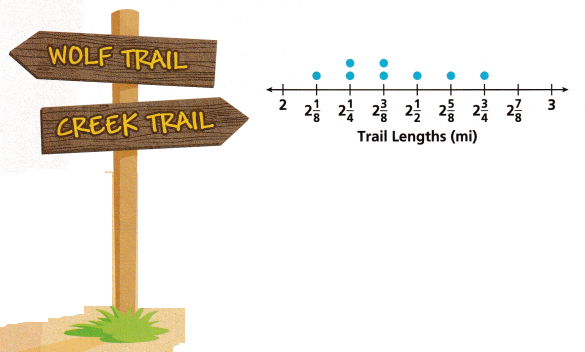
- Wolf Trait is longest, and tree Trail is shortest
- Pine Trait is \(\frac{3}{8}\) mile longer than Creek Trail.
- Deer Trait is longer than Pine Trail.
- North Trait is \(\frac{1}{4}\)-mile shorter than Pine Trail.
- Ridge Trail and Summit Trail are the same length.
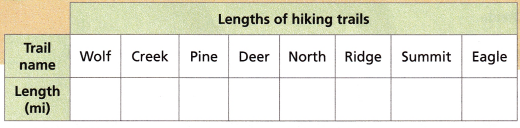
Answer:
wolf trail is the longest = 3 and creek trail = 2
Pine Trait is \(\frac{3}{8}\) + 2
Pine Trait = \(\frac{19}{8}\) = 2 \(\frac{3}{8}\)
Deer Trait > pine trail
Deer Trait = 2 \(\frac{7}{8}\)
North Trait = \(\frac{19}{8}\) – \(\frac{1}{4}\)
North Trait = \(\frac{17}{8}\) = 2\(\frac{1}{8}\)
Ridge Trail = Summit Trail
Ridge Trail = 2\(\frac{5}{8}\) + 2\(\frac{1}{4}\) = 2.625 + 2.25 = 4.875
Summit trail = 2.125 + 2.75 = 4.875 = 2 1/8 + 2 3/4
Eagle = 2 1/2
Explanation:
Turn and Talk
Question 1.
Explain how you determined the length of the Deer Trail.
Answer:
Deer Trait is larger than pine trail
The pine trail is 2 \(\frac{3}{8}\). So we need to select larger than the given number. Hence by comparing all other Trails we can determine the length of the Deer Trail is 2 \(\frac{7}{8}\).
Question 2.
Explain how you determined the lengths of Ridge Trail and Summit Trail.
Answer:
Ridge Trail and Summit Trail are the same lengths.
From the given figure we need to select Trail lengths.
Hence we can select 2\(\frac{5}{8}\) + 2\(\frac{1}{4}\) to calculate Ridge Trail. The answer is 4 \(\frac{7}{8}\).
Next, we can select 2\(\frac{1}{8}\) + 2\(\frac{3}{4}\) to calculate Summit trail. The answer is 4 \(\frac{7}{8}\).
Therefore both the trails have the same lengths.
Are You Ready?
Complete these problems to review prior concepts and skills you will need for this module.
Make and Interpret Line Plots
For Problems 1-4, use the following information.
An art teacher has a bag of ribbon pieces. The ribbon pieces are measured to the nearest \(\frac{1}{8}\) foot. The length of each piece is shown in the line plot.
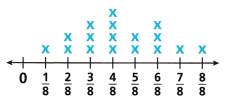
Question 1.
How many pieces of ribbon measure less than \(\frac{1}{2}\) foot?
Answer:
\(\frac{3}{4}\).
Explanation:
\(\frac{1}{8}\) + \(\frac{2}{8}\) + \(\frac{3}{8}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\).
Hence there are \(\frac{3}{4}\) pieces of ribbon measure less than \(\frac{1}{2}\) foot.
Question 2.
How many pieces of ribbon measure greater than \(\frac{1}{2}\) foot?
Answer:
\(\frac{9}{4}\).
Explanation:
There are \(\frac{9}{4}\) pieces of ribbon measure greater than \(\frac{1}{2}\) foot.
Question 3.
What is the difference in length between the longest and the shortest piece of ribbon?
Answer:
1 – \(\frac{1}{8}\) foot = \(\frac{7}{8}\).
Explanation:
The difference in length between the longest and the shortest piece of ribbon is \(\frac{7}{8}\).
Question 4.
How many pieces of ribbon measure at least \(\frac{3}{4}\) foot?
Answer:
\(\frac{1}{8}\) + \(\frac{2}{8}\) + \(\frac{3}{8}\) + \(\frac{4}{8}\) + \(\frac{5}{8}\) = \(\frac{3}{4}\)
Division Involving Decimals
Divide.
Question 5.
![]()
Answer:
$2.06
Explanation:
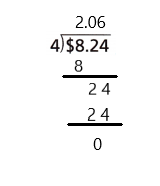
Question 6.
![]()
Answer:
2.23
Explanation:
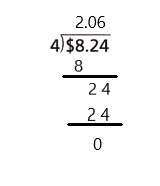
Question 7.
![]()
Answer:
$5.7
Explanation:
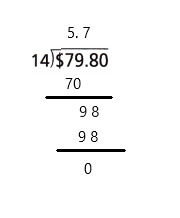
Write the fraction as a decimal.
Question 8.
\(\frac{40}{16}\) __________
Answer:
2.5
Explanation:
The fraction as a decimal is 2.5
\(\frac{40}{16}\) = \(\frac{5}{2}\) = 2.5
Question 9.
\(\frac{108}{16}\) ____________
Answer:
6.75
Explanation:
The fraction as a decimal is 6.75.
\(\frac{108}{16}\) = \(\frac{27}{4}\)
Question 10.
\(\frac{115}{8}\) ____________
Answer:
14.375
Explanation:
The fraction as a decimal is 14.375.
Write the mixed number as a decimal.
Question 11.
80\(\frac{2}{5}\) ____________
Answer:
80.4
Explanation:
Let us solve the given number
80\(\frac{2}{5}\) = \(\frac{402}{5}\)
80.4
Question 12.
20\(\frac{4}{16}\) ____________
Answer:
20.25
Explanation:
Let us solve the given number
20\(\frac{4}{16}\) = \(\frac{324}{16}\)
20.25
Question 13.
110\(\frac{9}{12}\) ____________
Answer:
110.75
Explanation:
Let us solve the given number
110\(\frac{9}{12}\) = \(\frac{1329}{12}\)
110.75