We included HMH Into Math Grade 5 Answer Key PDF Module 7 Lesson 1 Use Benchmarks and Number Sense to Estimate to make students experts in learning maths.
HMH Into Math Grade 5 Module 7 Lesson 1 Answer Key Use Benchmarks and Number Sense to Estimate
I Can use benchmarks to estimate a sum or difference of fractions with unlike denominators.
Spark Your Learning
Ms. Fong mixes water, glue, and laundry detergent together to make slime. The amount of each ingredient is a fraction of a liter.
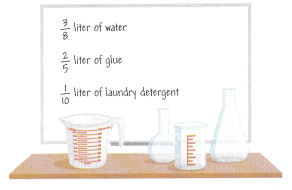
Use a visual model to estimate the total number of liters of ingredients she mixes together.

Answer:
\(\frac{3}{8}\) + \(\frac{2}{5}\) + \(\frac{1}{10}\)
\(\frac{3}{8}\) + \(\frac{4}{10}\) + \(\frac{1}{10}\)
\(\frac{3}{8}\) + \(\frac{5}{10}\)
The fractions have unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCD of 8 and 10 is 40.
\(\frac{3}{8}\) × \(\frac{5}{5}\) + \(\frac{5}{10}\) × \(\frac{4}{4}\)
\(\frac{15}{40}\) + \(\frac{20}{40}\) = \(\frac{35}{40}\) = \(\frac{7}{8}\)
Turn and Talk Describe whether each addend is closest to 0, \(\frac{1}{2}\), or 1.
Answer:
The solution is close to 1. Because 7/8 is approximately equal to 1.
Build Understanding
1. Ms. Fong has some bottles of copper powder for science experiments. She uses \(\frac{7}{8}\) bottle, \(\frac{2}{3}\) bottle, and \(\frac{5}{12}\) bottle. About how many bottles of copper powder does she use?

A. What expression represents the situation?
_______________
B. How can you use the three number lines and the benchmarks 0, \(\frac{1}{2}\) and 1 to help you estimate the answer?
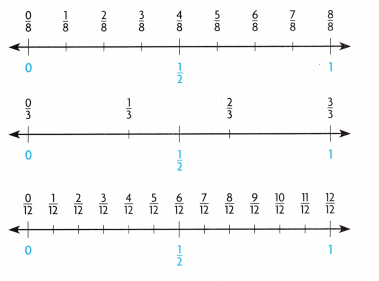
C. What expression represents the estimate?
Ms. Fong uses about ___ bottles of copper powder.
Answer:
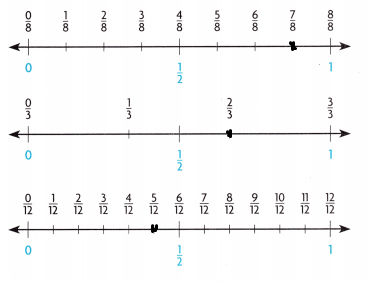
7/8 + 2/3 + 5/12 = 1.8
Ms. Fong uses about 2 bottles of copper powder.
Turn and Talk Without using a number line, how could you determine whether \(\frac{7}{8}\) and \(\frac{5}{12}\) are each closest to 0, \(\frac{1}{2}\), or 1 ?
Answer:
\(\frac{7}{8}\) = 0.8
\(\frac{5}{12}\) = 0.4
0.8 + 0.4 = 1.2
So, it is closest to 1.
Step It Out
2. Each group in science class has a 2-liter container of distilled water. Group A uses 1\(\frac{9}{10}\) L and Group B uses 1\(\frac{3}{8}\) L. About how much more distilled water does Group A use than Group B?
A. Represent the situation with an expression. ________
B. Determine an estimate without finding an exact answer.
- Between which two whole numbers does 1\(\frac{9}{10}\) lie? ____
- Is the fractional part of the mixed number closest to 0, \(\frac{1}{2}\), or 1 ? Explain.
- What whole number can you use to estimate 1\(\frac{9}{10}\)?
- Use benchmark values to estimate 1\(\frac{3}{8}\). ____
- Write an equation to estimate the difference.
C. About how much more distilled water does Group A use than Group B?
Answer:
Each group in science class has a 2-liter container of distilled water.
Group A uses 1\(\frac{9}{10}\) L and Group B uses 1\(\frac{3}{8}\) L.
1\(\frac{9}{10}\) – 1\(\frac{3}{8}\)
1\(\frac{9}{10}\) lies between 1 and 2.
The estimated whole number of 1\(\frac{9}{10}\) is 2.
The benchmark values to estimate 1\(\frac{3}{8}\) is 1.5
1\(\frac{9}{10}\) – 1\(\frac{3}{8}\)
1 + \(\frac{9}{10}\) – 1 – \(\frac{3}{8}\)
\(\frac{9}{10}\) – \(\frac{3}{8}\)
LCD is 10 and 8 is 40.
\(\frac{36}{40}\) – \(\frac{15}{40}\) = \(\frac{21}{40}\)
Thus Group A use \(\frac{21}{40}\) than Group B.
Check Understanding Math Board
Question 1.
A weather station reports that \(\frac{11}{12}\) foot of snow fell yesterday afternoon and \(\frac{1}{3}\) foot fell yesterday evening. Estimate the amount of snow that fell yesterday. ________
Answer:
Given,
A weather station reports that \(\frac{11}{12}\) foot of snow fell yesterday afternoon and \(\frac{1}{3}\) foot fell yesterday evening.
\(\frac{11}{12}\) + \(\frac{1}{3}\)
LCD is 12 and 3 is 12.
\(\frac{11}{12}\) + \(\frac{4}{12}\) = \(\frac{15}{12}\) = \(\frac{5}{4}\) = 1\(\frac{1}{4}\)
The amount of snow that fell yesterday is 1\(\frac{1}{4}\) foot.
Use benchmark values to write an expression to represent an estimate.
Question 2.
\(\frac{9}{10}\) + \(\frac{1}{12}\)
Answer: \(\frac{59}{60}\)
The denominator of both the fractions are not same.
So we have to find the LCD of the fractions and then add the fractions.
\(\frac{9}{10}\) + \(\frac{1}{12}\)
LCD is 10 and 12 is 60.
\(\frac{54}{60}\) + \(\frac{5}{60}\) = \(\frac{59}{60}\)
Question 3.
\(\frac{5}{8}\) – \(\frac{3}{5}\)
Answer:
\(\frac{5}{8}\) – \(\frac{3}{5}\)
The denominator of both the fractions are not same.
So we have to find the LCD of the fractions and then subtract the fractions.
LCD of 8 and 5 is 40.
\(\frac{25}{40}\) – \(\frac{24}{40}\) = \(\frac{1}{40}\)
On Your Own
Question 4.
History In the 1800s, wagon trains traveled west along the Oregon Trail. A wagon train traveled from Missouri to Wyoming in 1\(\frac{2}{3}\) months, and from Wyoming to Utah in \(\frac{3}{5}\) month. About how many months did it take the wagon train to travel from Missouri to Utah?
Answer:
Given,
A wagon train traveled from Missouri to Wyoming in 1\(\frac{2}{3}\) months, and from Wyoming to Utah in \(\frac{3}{5}\) month.
1\(\frac{2}{3}\) + \(\frac{3}{5}\)
1 + \(\frac{2}{3}\) + \(\frac{3}{5}\)
LCS of 3 and 5 is 15.
\(\frac{2}{3}\) + \(\frac{3}{5}\)
\(\frac{10}{15}\) + \(\frac{9}{15}\) = \(\frac{19}{15}\) = 1\(\frac{4}{15}\)
1 + 1\(\frac{4}{15}\) = 2\(\frac{4}{15}\)
Use benchmarks to estimate the sum or difference.
Question 5.
1\(\frac{5}{12}\) – \(\frac{2}{3}\) = ____
Answer:
Rewriting our equation with parts separated
1 + \(\frac{5}{12}\) – \(\frac{2}{3}\)
The denominators of the fractions are not same so we have to find the LCD.
LCD of 12 and 3 is 12
\(\frac{5}{12}\) – \(\frac{8}{12}\) = –\(\frac{3}{12}\)
1 – \(\frac{3}{12}\) = \(\frac{3}{4}\)
Question 6.
\(\frac{7}{10}\) + \(\frac{7}{8}\) = ____
Answer:
Rewriting our equation with parts separated
\(\frac{7}{10}\) + \(\frac{7}{8}\)
The denominators of the fractions are not the same so we have to find the LCD.
LCD of 10 and 8 is 40
\(\frac{28}{40}\) + \(\frac{35}{40}\) = \(\frac{63}{40}\)
\(\frac{63}{40}\) = 1 \(\frac{23}{40}\)
Question 7.
Use Tools Use the number lines and benchmarks to estimate 1\(\frac{1}{3}\) – \(\frac{5}{6}\).
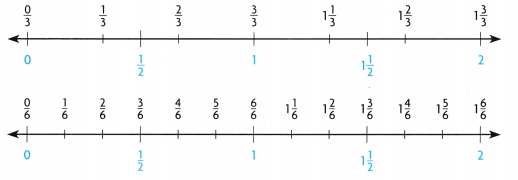 mix
mix
Estimate. Then compare the distance between each number and its benchmark. What does this tell you about the actual difference?
Answer:
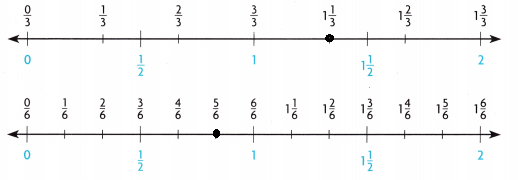
1\(\frac{1}{3}\) – \(\frac{5}{6}\)
1 + \(\frac{1}{3}\) – \(\frac{5}{6}\)
The denominators of the fractions are not the same so we have to find the LCD.
LCD of 3 and 6 is 6.
\(\frac{1}{3}\) – \(\frac{5}{6}\)
\(\frac{2}{6}\) – \(\frac{5}{6}\) = –\(\frac{3}{6}\) = –\(\frac{1}{2}\)
1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Question 8.
Open Ended Use mixed numbers or fractions with unlike denominators to write an addition expression and a subtraction expression, each with an estimate of 1\(\frac{1}{2}\). Justify your answer.
Answer:
2 \(\frac{1}{3}\) – \(\frac{5}{6}\)
Rewriting our equation with parts separated
2 + \(\frac{1}{3}\) – \(\frac{5}{6}\)
The denominators of the fractions are not the same so we have to find the LCD.
LCD of 3 and 6 is 6.
\(\frac{2}{6}\) – \(\frac{5}{6}\) = –\(\frac{3}{6}\) = –\(\frac{1}{2}\)
2 – \(\frac{1}{2}\) = 1\(\frac{1}{2}\)
I’m in a Learning Mindset!
Are the visual models effective in solving the problem?