We included HMH Into Math Grade 5 Answer Key PDF Module 20 Lesson 2 Classify and Organize Triangles to make students experts in learning maths.
HMH Into Math Grade 5 Module 20 Lesson 2 Answer Key Classify and Organize Triangles
I Can classify triangles.
Spark Your Learning
The house shown is called an A-frame house. Architects use triangular shapes in many building designs.

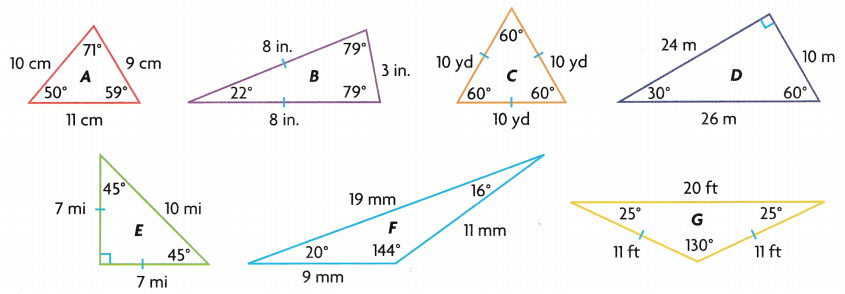
Group the triangles according to their attributes.
Answer:
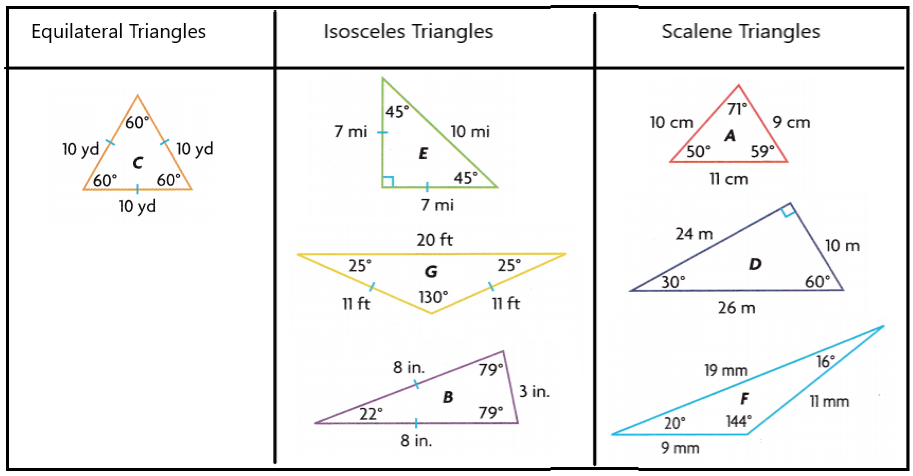
Explanation:
I grouped the above triangles based on whether they have all sides with equal length or 2 of the sides equal or different lengths of sides.
Turn and Talk Draw a square. Use a ruler to draw a diagonal line to form two triangles. Describe your triangles.
Answer:
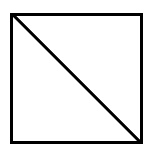
Explanation:
I drew a square and drew a diagonal line to form two triangles.
My triangles are isosceles triangles.
Build Understanding
Question 1.
The angles of the roofs on buildings can form many different types of triangles. Complete the tables by classifying the triangles by angle measures and by side lengths. Write acute (greater than 0° and less than 90°), obtuse (greater than 90° and less than 180°), or right (equal to 90°). Then write isosceles, scalene, or equilateral.
Connect to Vocabulary
Triangles can be classified by their angle measures and also by their side lengths.
An equilateral triangle has three congruent sides.
An isosceles triangle has at least two congruent sides.
A scalene triangle has no congruent sides.
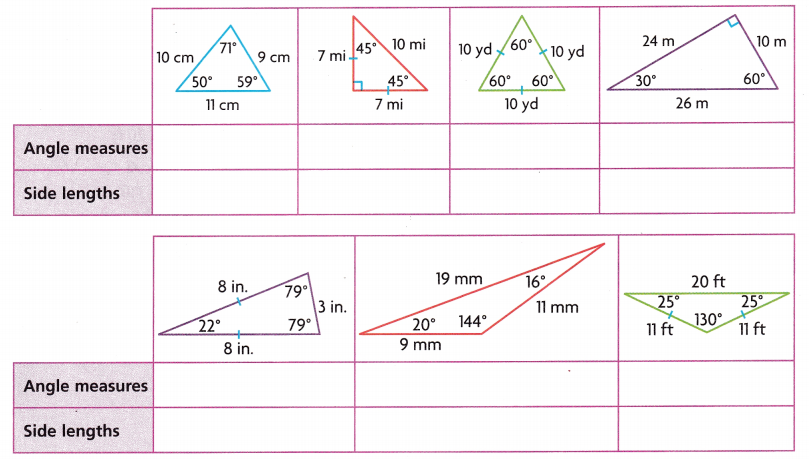
Answer:
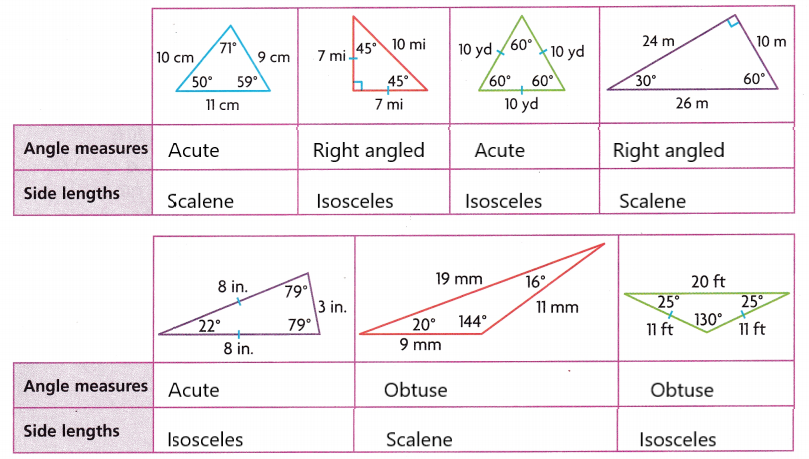
A. What do the angles of the right triangles and the obtuse triangles have in common?
Answer:
The sum of all the angles of both right triangles and obtuse triangles is 180.
B. Is it possible to draw a triangle that is both obtuse and equilateral? Explain.
Answer:
No, an equilateral triangle cannot have an obtuse angle as all the angles are fixed, they are each 60 degrees.
Turn and Talk Are equilateral triangles also isosceles triangles? Are all isosceles triangles also equilateral triangles? Explain.
Answer:
Every equilateral triangle is also an isosceles triangle.
No, Isosceles triangles have two sides to be equal length, while equilateral triangles have 3 sides of equal length.
Step It Out
Question 2.
Draw and name a triangle with exactly two congruent side and all angles smaller than a right angle.
A. Name the first attribute of the triangle given. Then draw that part of the triangle.
Answer:
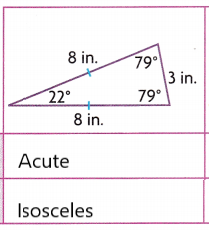
Explanation:
The first attribute is it is isosceles triangle
Two sides are of same length
B. Name the second attribute. Then complete the drawing of the triangle.
Answer:

Explanation:
The second attribute is all the angles are acute angles that is less than right angle
C. Classify the triangle you drew by its angles and by its sides.
Answer:
The triangle is isosceles and acute angled triangle.
Check Understanding
Question 1.
Each floor of the Flatiron building in New York City is shaped like a triangle. Look at this blueprint of one of the floors. Which terms best describe the shape of the floor? Explain your reasoning.

Answer:
Right triangle
Explanation:
Each floor of the Flatiron building in New York City is shaped like a triangle
The blue print of one of the floors is like a right triangle
So, it is the best term to describe the shape of the floor of Flatiron Building in New York City.
Classify the triangle. Write acute, obtuse, or right. Then write isosceles, scalene, or equilateral.
Question 2.
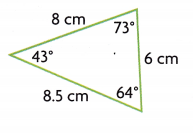
Answer:
Acute and scalene triangle
Explanation:
All the angles are less than right angle
All the sides are of different lengths
So, it is a acute and scalene triangle.
Question 3.
angles: 100°, 23°, 57°
sides: 20 yd, 8 yd, 17 yd
Answer:
Obtuse and scalene triangle
Explanation:
One of the angle is more than right angle
All the sides are of different lengths
So, it is an obtuse and scalene triangle.
On Your Own
Question 4.
Construct Arguments Tyler and Kiara each draw a line segment on the same isosceles triangle to form smaller triangles. Are their smaller triangles isosceles? Explain.
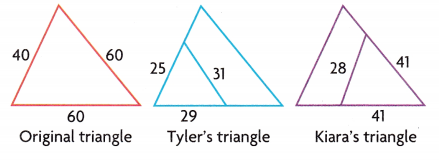
Answer:
No, Tyler’s small triangle is not isosceles and the Kiara’s small triangle is isosceles
Explanation:
Tyler and Kiara each draw a line segment on the same isosceles triangle to form smaller triangles
All the sides of Tyler’s small triangle are of different length
So, Tyler’s small triangle is not isosceles
Two of the sides of Kiara’s triangle are of same lengths
So, Kiara’s small triangle is isosceles.
Use structure Classify the triangle. Write acute, obtuse, or right. Then write isosceles, scalene, or equilateral.
Question 5.
angles: 45°, 90°, 45°
sides: 5 cm, 7 cm, 5 cm
Answer:
Right and scalene triangle
Explanation:
One of the angles of the three angles is 90
All the sides are of different sides
So, it is a right and scalene triangle.
Question 6.
angles: 13°, 20°, 147°
sides: 10 ft, 15 ft, 24 ft
Answer:
Obtuse and scalene triangle
Explanation:
One of the angle is more than right angle
All the sides are of different lengths
So, it is an obtuse and scalene triangle.
Question 7.
Attend to Precision Compare the triangles

Name one attribute that three of the triangles have in common.
Answer:
2 sides of 3 triangles A, C and D are of equal length
There are 3 isosceles triangles
Name one attribute that only one of the triangles has.
Answer:
All sides of the triangle A are equal
It is an equilateral triangle.
I’m in a Learning Mindset!
What parts of classifying triangles am I comfortable finding on my own?
Answer:
Am comfortable in classifying the sides of the triangles by my own.