We included HMH Into Math Grade 5 Answer Key PDF Module 11 Review to make students experts in learning maths.
HMH Into Math Grade 5 Module 11 Review Answer Key
Concepts and Skills
Question 1.
Write a word problem that can be modeled by the equation 2 ÷ \(\frac{1}{8}\) = m. Then draw a visual fraction model to represent and solve the problem.
Answer:
Word problem:
“There are 2 cakes each cake piece is of \(\frac{1}{8}\) part so how many parts are there?”,
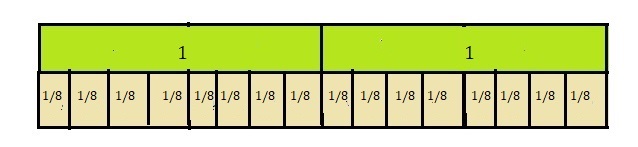
16 parts or 16 pieces of cakes,
Explanation:
Given to write a word problem that can be modeled by the equation 2 ÷ \(\frac{1}{8}\) = m.
Word problem:
“There are 2 cakes each cake piece is of \(\frac{1}{8}\) part so how many parts are there?”,
Drawn a visual fraction model to represent and solving the problem as m = 2 ÷ \(\frac{1}{8}\) = 2 X 8 = 16 parts or 16 pieces of cake.
Question 2.
Usain has \(\frac{1}{2}\) bag of cat food. He feeds an equal amount of the bag to his cat each day for 8 days. What fraction of the whole bag does he feed his cat each day? Write a division equation and a related multiplication equation to solve.
Answer:
Division equation:
f= \(\frac{1}{2}\) ÷ 8,
Multiplication equation:
f = \(\frac{1}{2}\) X \(\frac{1}{8}\),
Each day Usain feed \(\frac{1}{16}\) bag of cat food
Explanation:
Given Usain has \(\frac{1}{2}\) bag of cat food.
He feeds an equal amount of the bag to his cat each day for 8 days. let f be the fraction of the whole bag does he feed his cat each day a division equation is
f= \(\frac{1}{2}\) ÷ 8 and a related multiplication equation is f = \(\frac{1}{2}\) X \(\frac{1}{8}\),
Solving f = \(\frac{1}{2 X 8}\) = \(\frac{1}{16}\), Therefore each day Usain feed \(\frac{1}{16}\) bag of cat food.
Question 3.
Use Tools Sienna is making origami stars. Each star uses a strip of paper. She has 36 sheets of origami paper, and cuts out strips that are \(\frac{1}{2}\) of each sheet. How many origami stars can Sienna make? Tell what strategy or tool you will use to answer the question, explain your choice, and then find the answer.
Answer:
Sienna makes 72 stars,
short division,
Explanation:
Given Sienna is making origami stars. Each star uses a strip of paper. She has 36 sheets of origami paper and cuts out strips that are \(\frac{1}{2}\) of each sheet.
Number of origami stars can Sienna make using short division strategy as 36 ÷ \(\frac{1}{2}\) because 36 sheets are cut into \(\frac{1}{2}\) strips so we use short division to find number of origami stars solving we get
36 ÷ \(\frac{1}{2}\) = 36 X 2 = 72 stars.
Question 4.
Which division equation correctly represents the number line?

(A) \(\frac{1}{4}\) ÷ 3 = x
(B) \(\frac{1}{3}\) ÷ 4 = x
(C) 3 ÷ \(\frac{1}{4}\) = x
(D) 4 ÷ \(\frac{1}{3}\) = x
Answer:
(B) \(\frac{1}{3}\) ÷ 4 = x,
Explanation:
The division equation that correctly represented on the number line is as the blue mark is showing from
0 to \(\frac{1}{3}\) and is divided by 4 which matches with (B) \(\frac{1}{3}\) ÷ 4 = x.
Question 5.
Use the expression \(\frac{1}{2}\) ÷ 12 to complete the word problem. Then draw a visual fraction model to represent and solve the problem.
Trevor has ___________ days to finish Illustrating ____________ of a book. If the time he spends illustrating is an equal amount each day, how much of the whole book will Trevor illustrate each day?
Answer:
Word problem:
“Trevor has 12 days to finish Illustrating \(\frac{1}{2}\) of a book If the time he spends illustrating is an equal amount each day,
how much of the whole book will Trevor illustrate each day?”,

Trevor illustrate \(\frac{1}{24}\) each day,
Explanation:
Used the expression \(\frac{1}{2}\) ÷ 12 to complete the word problem as
“Trevor has 12 days to finish Illustrating \(\frac{1}{2}\) of a book If the time he spends illustrating is an equal amount each day, how much of the whole book will Trevor illustrate each day?”,
Then drawn a visual fraction model to represent and solving the problem as \(\frac{1}{2}\) ÷ 12 =
\(\frac{1}{2}\) X \(\frac{1}{12}\) = \(\frac{1}{2 X 12}\) = \(\frac{1}{24}\),
therefore Trevor illustrate \(\frac{1}{24}\) each day.
Divide. Write a related multiplication equation to solve.
Question 6.
11 ÷ \(\frac{1}{5}\) = n
Answer:
Multiplication equation:
11 X 5 = n,
n = 55,
Explanation:
Given 11 ÷ \(\frac{1}{5}\) = n to write the related multiplication equation it is
n = 11 X 5 we will get n = 55.
Question 7.
n = \(\frac{1}{3}\) ÷ 18
Answer:
Multiplication equation:
n = \(\frac{1}{3}\) X \(\frac{1}{18}\),
n = \(\frac{1}{54}\),
Explanation:
Given n = \(\frac{1}{3}\) ÷ 18 to write the related multiplication equation it is
n = \(\frac{1}{3}\) X \(\frac{1}{18}\)
we will get n = \(\frac{1}{3 X 18}\),
n = \(\frac{1}{54}\).
Question 8.
Fiona’s mom makes \(\frac{1}{4}\) gallon of raspberry lemonade for Fiona and her 3 friends for a picnic lunch. Select all the equations that represent the fraction of a gallon of raspberry lemonade that Fiona and her 3 friends will each get.
(A) \(\frac{1}{4}\) × \(\frac{1}{4}\) = r
(B) \(\frac{1}{4}\) × \(\frac{1}{3}\) = r
(C) 3 ÷ \(\frac{1}{4}\) = r
(D) 4 ÷ \(\frac{1}{4}\) = r
(E) \(\frac{1}{4}\) ÷ 4 = r
(F) \(\frac{1}{4}\) × 3 = r
Answer:
Bits (B) \(\frac{1}{4}\) × \(\frac{1}{3}\) = r and
(F) \(\frac{1}{4}\) × 3 = r matches with fraction of a gallon of raspberry lemonade that Fiona and her 3 friends will each get,
Explanation:
Given Fiona’s mom makes \(\frac{1}{4}\) gallon of raspberry lemonade for Fiona and her 3 friends for a picnic lunch. Selecting all the equations that represent the fraction of a gallon of raspberry lemonade that Fiona and her 3 friends will each get as \(\frac{1}{4}\) ÷ 3 = r,
Solving we will get r = \(\frac{1}{4}\) X \(\frac{1}{3}\),
r = \(\frac{1}{4 X 3}\) = \(\frac{1}{12}\).
Checking with bit (A) \(\frac{1}{4}\) × \(\frac{1}{4}\) = r,
r = \(\frac{1}{4 X 4}\) = \(\frac{1}{16}\) which will not matche as \(\frac{1}{16}\) ≠ \(\frac{1}{12}\),
Checking with bit (B) \(\frac{1}{4}\) × \(\frac{1}{3}\) = r,
r = (B) \(\frac{1}{4 x 3}\) = \(\frac{1}{12}\) matches,
Checking with bit (C) 3 ÷ \(\frac{1}{4}\) = r, r= 3 X 4 = 12 which will not match as 12 ≠ \(\frac{1}{12}\),
Checking with bit (D) 4 ÷ \(\frac{1}{4}\) = r, r = 4 X 4 = 16 which will not match as 14 ≠ \(\frac{1}{12}\).
Checking with bit (E) \(\frac{1}{4}\) ÷ 4 = r,
r = \(\frac{1}{4}\) X \(\frac{1}{4}\),
r = \(\frac{1}{4 X 4}\) = \(\frac{1}{16}\) which will not match as \(\frac{1}{16}\) ≠ \(\frac{1}{12}\),
Checking with bit (F) \(\frac{1}{4}\) × 3 = r,
r = \(\frac{1}{4}\) X \(\frac{1}{3}\) =
\(\frac{1}{4 X 3}\) = \(\frac{1}{12}\) matches.
So bit (B) \(\frac{1}{4}\) × \(\frac{1}{3}\) = r and
(F) \(\frac{1}{4}\) × 3 = r matches with fraction of a gallon of raspberry lemonade that Fiona and her 3 friends will each get.