We included HMH Into Math Grade 4 Answer Key PDF Module 3 Lesson 3 Use Division to Solve Multiplicative Comparison Problems to make students experts in learning maths.
HMH Into Math Grade 4 Module 3 Lesson 3 Answer Key Use Division to Solve Multiplicative Comparison Problems
I Can solve a multiplicative comparison problem by using division with drawings and equations.
Step It Out
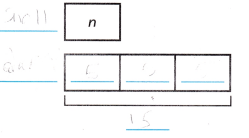
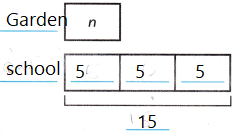
1. Olivia is in the photography club. She takes 15 photos at a garden. That is 3 times as many
photos as she takes at school. How many photos does Olivia take at school?
A. Use a bar model to show the problem.
Let n represent the unknown.

Explanation:
B. Write an equation to model the problem. Use n for the unknown.
Problem: 3 times as many as n is 15.
Equation: __ × n = ___
Explanation:
5 x 3 = 15
15 ÷ 3 = 15
Connect to Vocabulary
Inverse operations, such as multiplication and division, undo each other.
3 × 26
6 ÷ 3 = 2
C. Use the inverse operation to solve the problem.
___ ÷ ___ = n
___ = n
Explanation:
15 ÷ 3 = n
5 = n
D. Olivia takes ___ photos at school.
Explanation:
Olivia takes 5 photos at school.
Turn and Talk How did you represent 3 times as many in your bar model and equations?
Explanation:
By following the division equation.
Step It Out
2. This year, 28 students are in the chess club. Last year, 7 students were in the dub. How many times as many students are in the chess club this year than last year?

A. Write a multiplication equation to model the problem. Use n for the unknown.
n × __ = __
Explanation:
n x 4 = 28
7 x 4 = 28
B. Write a division equation to solve the problem.
___ ÷ ___ = ___
___ = n
Explanation:
28 ÷ 7 = 4
4 = n
This year, 4 times as many students are in the chess club.
Turn and Talk Why can you use division to solve a multiplicative comparison problem, but not an additive comparison problem?
Explanation:
One way you might describe the difference between the two is this. Additive comparisons. You focus on the difference between the two quantities. With multiplicative comparison, you focus on how many times larger or smaller one quantity is compared to the other.
Check Understanding Math Board
Write multiplication and division equations to model and solve the problem. Use n for the unknown.
Question 1.
Leslie collects 24 aluminum cans and 8 glass bottles for the recycling club. How many times as many cans as bottles does Leslie collect?
Leslie collects ___ times as many cans as bottles.
Answer:
n x 8 = 24
4 x 8 = 24
24 ÷ 8 = 4
Explanation:
Leslie collects 4 times as many cans as bottles.
Question 2.
The students in the cooking club bake 12 blueberry muffins. They bake twice as many blueberry muffins as corn muffins. How many corn muffins do the students bake?
The students bake ___ corn muffins in the cooking club.
Answer:
n x 2 = 12
6 x 2 = 12
12 ÷ 2 = 6
Explanation:
The students bake 6 corn muffins in the cooking club.
On Your Own
Question 3.
Use Tools The library club receives 56 fiction books and 8 nonfiction books. How many times as many fiction books as nonfiction books does the club receive?
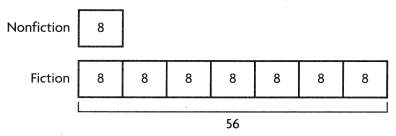
Answer:
56 ÷ 8 = 7
7 x 8 = 56
Explanation:
7 times as many fiction books as nonfiction books that the club receive
Question 4.
Use Structure Bob fills a basket with carnations and roses. He uses 18 roses and twice as many roses as carnations. How many carnations does Bob use?

• Write an equation to model the problem.
____ ![]() n = ____
n = ____
• Use the inverse operation to write a different equation and solve the problem.
____ ![]() ___ = n
___ = n
Answer:
2 x n = 18
9 x 2 = 18
18 ÷ 2 = 9
Explanation:
9 carnations that Bob use
Question 5.
Model with Mathematics A sweater costs $40. That is 5 times as much as a shirt. What is the price of the shirt ? Write multiplication and division equations to model and solve the problem. Use s for the unknown.
Answer:
n x 5 = 40
8 x 5 = 40
40 ÷ 5 = 8
Explanation:
$8 is the price of the shirt.
Question 6.
Open Ended Write a multiplicative comparison word problem that can be modeled and solved with the equations 7 × m = 21 and 21 ÷ 7 = m.
Answer:
21 ÷ 7 = m.
m = 3
7 × m = 21
7 x 3 = 21
Explanation:
In a Dance studio they played a song for 21 minutes. That is 7 times as long as the normal song.
On Your Own
Question 7.
Use Tools In the martial arts club, students spend 20 minutes working on blocking. That is 4 times as long as they spend meditating. How many minutes do the students spend meditating?

- Complete the bar model to show the problem.
- Use inverse operations to write equations to model and solve the problem.
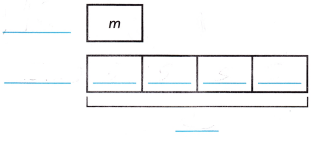
Answer:
n x 4 = 20
5 x 4 = 20
20 ÷ 4 = 5
Explanation:
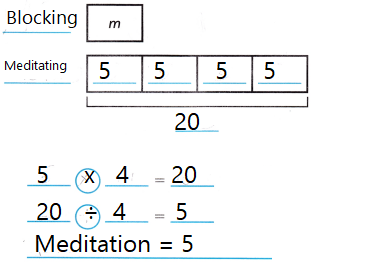
5 minutes that the students spend meditating
Question 8.
Students in the engineering club build two train tracks. Track A is 24 feet long. That is 3 times as long as the length of Track B. What is the length of Track B? Show your work.
___________________________
Answer:
n x 3 = 24
8 x 3 = 24
24 ÷ 3 = 8
Explanation:
length of Track B = 8 feet long.
Question 9.
Critique Reasoning Kevin walks 6 laps and jogs 2 laps. Kevin writes this equation to find how many times as many laps he walks as jogs. Is Kevin correct? Explain.

Answer:
No, kelvin is wrong
Explanation:
We have to do addition to find the number of laps here
Kevin walks 6 laps and jogs 2 laps.
6 + 2 = 8
8 is the correct answer.