We included HMH Into Math Grade 4 Answer Key PDF Module 13 Lesson 4 Relate Degrees to Fractional Parts of a Circle to make students experts in learning maths.
HMH Into Math Grade 4 Module 13 Lesson 4 Answer Key Relate Degrees to Fractional Parts of a Circle
I Can find the measure of an angle by using its fractional part of a circle.
Spark Your Learning
Based on what you know about the measurement of the shaded piece of the circle, how can you describe the measurement of the circle?


Answer:
90 degrees
Explanation:
Angle of complete circle is 360 degrees.
4 equal right angle make a circle.
Angle of right angle is 90 degrees.
So, the shaded part is 90 degrees.
Turn and Talk What other fractions can you use to describe the measurement of a circle?
Answer:
The measure of an angle is determined by the amount of rotation from the initial side to the terminal side.
One way to measure an angle is in terms of degrees .
A measure of one degree ( 1° ) is equivalent to a rotation of 1360 of a complete revolution.
Build Understanding
Question 1.
Circles can be divided into measurement units called degrees. How can you relate the fractional turns of a circle to degrees?
Answer:
90 degrees
Explanation:
Angles are measured in units called degrees. The symbol for degrees is °.
If a circle is divided into 360 equal parts, then an angle that turns through 1 part of the 360 measures 1°.
Fraction is a part of a whole.
Connect to Vocabulary
Angles are measured with reference to a circle as they turn around a center point. The size of the angle is the measure of how far one side is turned from the other side. Angles are measured in units called degrees. The symbol for degrees is °.
A. How can you write a fraction to represent the quarter turns in a circle?
- _______ is a quarter turn.
- _______ is two quarter turns.
- _______ is three quarter turns.
- _______ is four quarter turns.
_______ quarter turns make a full turn on a circle.
Answer:
- 90° is a quarter turn.
- 180° is two quarter turns.
- 270° is three quarter turns.
- 360° is four quarter turns.
four quarter turns make a full turn on a circle.
Explanation:
Circle is divided into 4 quarter, each quarter is of 90 degrees.
B. How can you show the number of eighth turns it takes to make a full turn on a circle?
Answer:
\(\frac{360}{8}\) = 45°
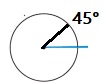
Explanation:
360° full turn in the circle.
The number of eighth turns to make a full turn on a circle is \(\frac{360}{8}\) = 45°
C. How many \(\frac{1}{120}\) turns would it take to make a full turn around the circle?
Answer:
\(\frac{1}{120}\) turns
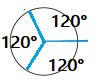
Explanation:
360° full turn in the circle.
The number of eighth turns to make a full turn on a circle is \(\frac{360}{3}\) = 120°
D. How many \(\frac{1}{360}\) turns would it take to make a full turn around the circle?
Think of a circle divided into 360 equal parts. An angle that turns through \(\frac{1}{360}\) 0f the circle measures 1 degree.

Answer:
360°
Explanation:
Angle of complete circle is 360 degrees, fraction of a whole is \(\frac{1}{360}\)
360° x \(\frac{1}{360}\) = 1°
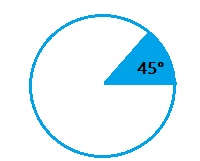
E. How can you use degrees to describe the measure of an angle that has eight \(\frac{1}{360}\) turns?
Answer:
45°
Explanation:
Angle of a circle is 360 degrees,
Eight turns of an angle is 45 degrees.
8 x \(\frac{1}{360}\)
= \(\frac{8}{360}\)
=45°
Question 2.
Drafters prepare technical drawings for all kinds of designs. A drafter draws this fractional part of a circle for a project. How can you find the measure of the angle in degrees?
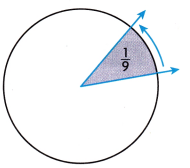
A. How can you think about the fractional part of the circle as degrees?
Answer:
40°
Explanation:
Angle of a circle is 360 degrees,
nine turns of an angle is 40 degrees
9 x \(\frac{360}{1}\)
= \(\frac{360}{9}\)
= 40°
B. How can you write \(\frac{1}{9}\) as an equivalent fraction with a denominator of 360?
Answer:
360 x \(\frac{1}{9}\) = 40
Explanation:
Angle of a circle is 360 degrees,
nine turns of an angle is 40 degrees
9 x \(\frac{360}{1}\)
= \(\frac{360}{9}\)
= 40°
C. The measure of the angle is __________.
Answer:
40 degrees
Explanation:
Angle of a circle is 360 degrees,
nine turns of an angle is 40 degrees
9 x \(\frac{360}{1}\)
= \(\frac{360}{9}\)
= 40°
Turn and Talk How can you describe the fraction of a circle through which a straight angle turns?
Answer:
Angles are measured with reference to a circle as they turn around a center point.
The size of the angle is the measure of how far one side is turned from the other side.
Angles are measured in units called degrees.
The symbol for degrees is °.
Connect to Vocabulary
acute—an angle that measures greater than 0 and less than 90°
right—an angle that measures 90°
obtuse—an angle that measures greater than 90° and less than 180°
straight—an angle that measures 180°
reflex—an angle that measures greater than 180°
Question 3.
Angles are named by the way that they relate to 0°, 90°, or 180°. What is a name for each angle?
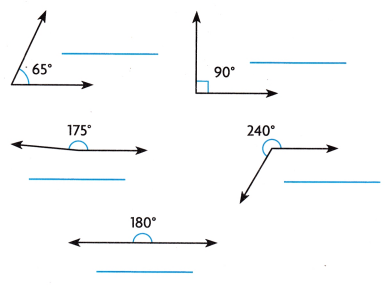
Answer:
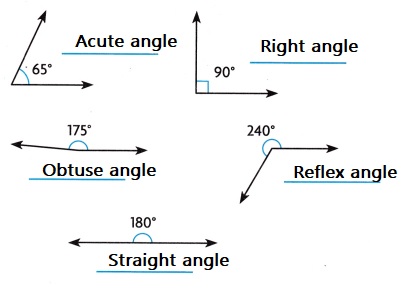
Explanation:
Angle less than 90 degrees is acute angle.
Angle greater than 90 degrees is obtuse angle.
Angle which measures 90 degrees is right angle.
Angle which measures 180 degrees is straight angle.
Angle which measures more than 180 degrees is reflex angle.
Turn and Talk How can you describe the fraction of a circle through which a straight angle turns?
Answer:
A complete or whole circle is taken as 1 and parts of the circles are represented as fractions.
Explanation:
An angle is a fraction of a circle where the whole circle is 360°.
A straight angle is the same as half the circle and is 180° whereas a right angle is a quarter of a circle and is 90°. Use the protractor to measure the size of an angle.
Step It Out
Question 4.
Architects often use circles when designing buildings. How can you find the measure of an angle from the fractional part of the circle formed by the window?
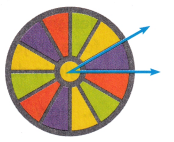
A. To estimate, describe the angle.
Answer:
30 degrees
Explanation:
Angle of complete circle is 360 degrees.
Whole is divided into 12 equal parts.
= \(\frac{360}{12}\)
= 30°
B. Determine the fraction of a circle that any one angle turns.
Answer:
The fraction of a circle that any one angle turns
C. Write an equivalent fraction to find the measure of the angle in degrees.
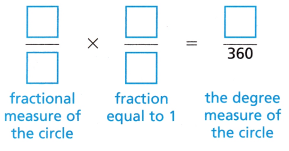
Answer:
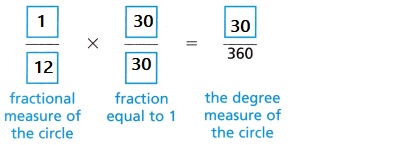
Explanation:
Angle of complete circle is 360 degrees.
Whole is divided into 12 equal parts.
= \(\frac{360}{12}\)
= 30°
D. The measure of the angle from the fractional part of the circle formed by the window is _______.
Answer:
30°
Explanation:
Angle of complete circle is 360 degrees.
Whole is divided into 12 equal parts.
= \(\frac{360}{12}\)
= 30°
Turn and Talk How did your description help you determine if your answer was reasonable?
Answer:
Angles are measured with reference to a circle as they turn around a center point.
The size of the angle is the measure of how far one side is turned from the other side.
Angles are measured in units called degrees.
The symbol for degrees is °, here the measure of an angle is 30°
Check Understanding
Question 1.
Write the measure of the shaded angle in degrees.
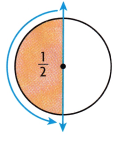
Answer:
Explanation:
The fraction of a circle that any one angle turns.
Complete angle of circle is 360 degrees.
Question 2.
Classify the angle. Write acute, right, obtuse, straight, or reflex.
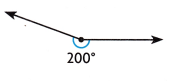
Answer:
Reflex angle
Explanation:
A reflex angle is any angle that is more than 180 degrees (half circle) and less than 360 degrees (full circle).
A reflex angle will always have either an obtuse or an acute angle on the other side of it.
It can be one of the more confusing angles to find because it’s on the ‘outside’ of the angle.
On Your Own
Question 3.
The answer is 90 full turns. What might the question be?
Answer:
What fraction of a circle is the measurement of 90 in a circle.
Explanation:
Complete circle is divided into 4 equal parts.
Angle of circle is 360 degrees.
Fraction of circle is
Question 4.
Why is a straight angle different from a reflex angle?
Answer:
A Straight angle or a half turn is always 180 °.
Reflex is the next largest measuring more than 180° but less than 360°.
Explanation:
Full rotation or full circle at 360°.
A reflex angle is always greater than a straight angle which is a half-circle (180°),
and less than a complete angle which is a full circle (360°).
Question 5.
What is the measure of the shaded angle? Through what fraction of the circle does the angle turn?
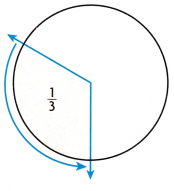
Estimate.
\(\frac{1}{3}\) = \(\frac{}{360}\) 3 × 12 = 36, so 3 × ________ = 360.
The measure of the angle is _________.
Was your estimate reasonable?
Answer:
\(\frac{1}{3}\) = \(\frac{}{360}\) 3 × 12 = 36, so 3 × 120 = 360.
The measure of the angle is 120°
Was your estimate reasonable?
yes, its reasonable.
Explanation:
Circle is divided into 3 equal parts.
Each fraction of a circle is \(\frac{1}{3}\)
Angle of a fraction is \(\frac{360}{3}\) = 120 degrees.
Tell the measure of the angle in degrees.
Question 6.
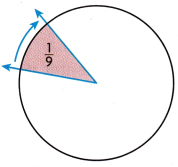
Answer:
The measure of the angle is 120°
Explanation:
whole is divided into 9 equal parts.
fraction of a whole is \(\frac{1}{9}\) x 360°
= \(\frac{360}{9}\) = 40°,
So, 9 × 40 =360.
The measure of the angle is 120°
Question 7.
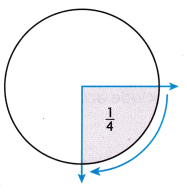
Answer:
The measure of the angle is 90°
Explanation:
Whole is divided into 4 equal parts,
fraction of a whole is \(\frac{1}{4}\) x 360°
= \(\frac{360}{4}\) = 90°,
so 4 × 90 =360.
The measure of the angle is 90°
Question 8.
Why is this angle not a straight angle?
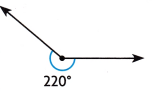
Answer:
The given angle is more than straight angle and less than a circle.
Explanation:
A reflex angle is any angle that is more than 180 degrees (half circle) and less than 360 degrees (full circle).
A reflex angle will always have either an obtuse or an acute angle on the other side of it.
It can be one of the more confusing angles to find because it’s on the ‘outside’ of the angle.
Classify the angle. Write acute, right, obtuse, straight, or reflex.
Question 9.
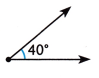
Answer:
Acute angle
Explanation:
An acute angle is defined as an angle that measures less than 90 degrees.
Question 10.
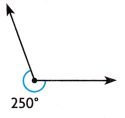
Answer:
Reflex angle
Explanation:
A reflex angle is any angle that is more than 180 degrees (half circle) and less than 360 degrees (full circle).
Question 11.
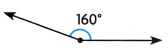
Answer:
Obtuse angle
Explanation:
Obtuse angle is an angle greater than 90°
Question 12.
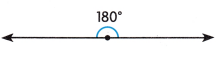
Answer:
Straight angle
Explanation:
A straight angle measures 180° it is an angle whose arms lie in opposite directions from the vertex and join together to form 180°.
Question 13.
History The Chicago Cultural Center was completed in 1897 and contains two detailed stained-glass ceiling domes. The Healy and Millet dome is on the north side of the building in the Grand Army of the Republic Hall and was designed and made by two talented artists.

How many parts fill the circle? ________
Answer:
8 parts
What is the measure of the angle of one fractional part of the stained-glass ceiling? _________
Answer:
45°
Explanation:
Whole is divided into 8 equal parts,
fraction of a whole is \(\frac{1}{8}\) x 360°
= \(\frac{360}{8}\) = 45°,
So, 8 × 45° =360
Question 14.
Open-Ended On a separate piece of paper, design a stained-glass window within a circle that has a center point. Include acute, right, obtuse, straight, and reflex angles.
Answer:
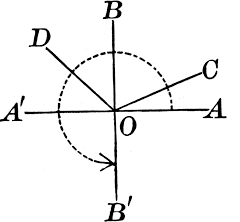
Explanation:
∠A’OD is an Acute angle — an angle that measures greater than 0 and less than 90°
∠AOB is a Right angle — an angle that measures 90°
∠DOC is a Obtuse angle — an angle that measures greater than 90° and less than 180°
∠A’OA is a Straight angle — an angle that measures 180°
∠AOB’ is a Reflex angle — an angle that measures greater than 180°
I’m in a Learning Mindset!
Are my efforts effective when I write an equation for the degree measure of an angle?
Answer:
Yes, they are effecctive efforts.
Explanation:
The conversion of measuring an angle from radians to degrees can be done using the following formula:
Angle in Radians × 180°/π = Angle in Degrees.