We included HMH Into Math Grade 3 Answer Key PDF Module 5 Lesson 1 Use the Distributive Property to make students experts in learning maths.
HMH Into Math Grade 3 Module 5 Lesson 1 Answer Key Use the Distributive Property
I Can use the Distributive Property to find a product when one factor is a multiple of lo.
Spark Your Learning
Three friends place 4 rows of 30 tiles each on a swimming pool floor. Each friend uses the Distributive Property to show the number of tiles they placed.
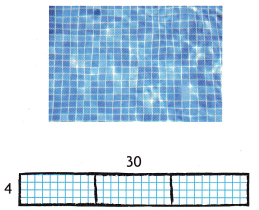
Gina says, “I showed a sum multiplied by a number.”
Roy says, “I showed a sum of 3 products.”
Bree says, “I showed the sum of 3 numbers.”
Show how each friend used the Distributive Property. Then write an equation to find the number of tiles.

Turn and Talk Which method of using the Distributive Property works best for you?
Build Understanding
1. Jamal is tiling a patio. He places 6 rows of tiles with 20 tiles in each row. How many tiles does he use?
Label the area model and complete the equations. Show how you can use the Distributive Property to find the product.
A. How can you show 6 rows of 20 on a grid? The rectangle you make on the grid is an area model.
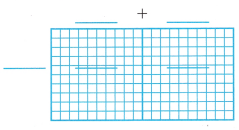
B. How can you break apart the factor 20 into multiples of 10? Show this on the area model. Label the area model.
___ + ___ = ____
C. How many tiles are in each smaller rectangle you made on the area model?
______________________
D. Why do you need to add the products of the two smaller rectangles?
6 × 20 = 6 × (___ + ___)
6 × 20 = (___ × ___) + (___ × ___)
6 × 20 = ___ + ___
6 × 20 = ____
Answer:
6 × 20 = 6 × (10 + 10)
6 × 20 = (6 × 10) + (6 × 10)
6 × 20 = 60 + 60
6 × 20 = 120
E. Complete the equations. How many tiles does Jamal use?
Turn and Talk Look back at Spark Your Learning. How do the friends’ statements compare to equations you used to find the number of tiles Jamal placed?
2. Trish places tiles on one wall of a swimming pool. There are 7 rows of tiles with 30 tiles in each row. How many tiles does Trish place on the wall?

A. How can you show 7 rows of 30 tiles on the area model?
B. How can you write the product as a sum multiplied by a number?
C. How can you write the product as a sum of three products?

D. How can you write the product as a sum of three numbers? _____
E. How many tiles does Trish place on the wall? ____
3. Elena decorates a swimming pool wall that has 5 rows of 40 tiles each. How many tiles does Elena use?
A. To find 5 × 40, show one way to break apart 40 into multiples of 10.
5 × 40 = __ × (__ + __ + __ + ___)
Answer:
5 × 40 = 5 × (10 + 10 + 10 + 10)
B. Show another way to break apart 40 into multiples of 10.
5 × 40 = ___ × (___ + ___)
Answer:
5 × 40 = 5 × (20 + 20)
C. How many tiles does Elena use? ___
Answer:
5 × 40 = 200
Thus Elena use 200 tiles.
Turn and Talk Explain how breaking apart a factor into multiples of 10 makes finding the product easier.
Step It Out
4. Philippe paves a walkway with stones. He uses 4 rows of stones with 40 stones in each row. How many stones does Philippe use?

4 rows of 40 = __ × ___
A. Draw and label the area model to break apart the multiple of 10 to make the problem easier to solve.
Answer:
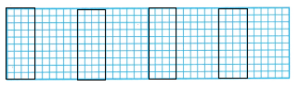
4 rows of 40 = 4 × 40
B. Write the products of the smaller rectangles.
(4 × 10) + (____) + (___ ) + (___)
Answer: (4 × 10) + (4 × 10) + (4 × 10) + (4 × 10)
C. Find the products, and then find the sum of the products.
Phillipe uses ___ stones.
Answer:
40 + 40 + 40 + 40 = 160
Phillipe uses 160 stones.
Check UnderstandingMath Board
Question 1.
Verna places 3 rows of tiles with 60 tiles in each row on a patio floor. Draw and label the area model to find the total number of tiles that Verna uses. ____

Answer:
Given,
Verna places 3 rows of tiles with 60 tiles in each row on a patio floor.
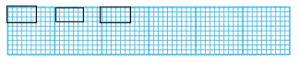
3 × 60 = 180 tiles
Write one way to break apart a factor into multiples of 10.
Question 2.
8 × 20
___ × (___ + ___)
Answer: 160
8 × ( 10 + 10 )
16 × 10
Sixteen tens.
Question 3.
3 × 50
___ × (___ + ____)
Answer: 150
3 × ( 25 + 25 )
150
Fifteen tens.
On Your Own
Question 4.
Construct Arguments Pam says that she can write 8 × 60 as the sum of two products. Is she correct? Explain.
Answer:
Given,
Pam says that she can write 8 × 60 as the sum of two products.
8 × (30 + 30)
Yes Pam is correct.
Use the Distributive Property to complete the equations. Then find the product.
Question 5.
8 × 20 = (___ × ___) + (__ × __)
8 × 20 = ___
Answer: 160
8 × 20 = ( 2 × 4 ) + ( 2 × 10 )
8 × 20 = 160
By multiplying 8 with 20 we get 160.
Question 6.
9 × 30 = (9 × 10) + (9 × __) + (9 × ___)
9 × 30 = __ x (__ + __ + _____)
9 × 30 = ____
Answer: 270.
9 × 30 = (9 × 10) + (9 × 10) + (9 × 10)
9 × 30 = 9 x (10+ 10 + 10)
9 × 30 = 270
By multiplying 9 with 30 we get 270
Question 7.
7 × 50 = 7 × (10 + 10 + __ + __ + ___)
7 × 50 = 7 × (__ + ___)
7 × 50 = ___
Answer: 450
7 × 50 = 7 × (10 + 10 + 10 + 10 + 10)
7 × 50 = 7 × (20 + 30)
7 × 50 = 450
By multiplying 7 with 50 we get 450.
Question 8.
2 × 90 = (2 × __) + (2 × __)
2 × 90 = __ + ___
2 × 90 = ___
Answer: 180
2 × 90 = (2 × 45 ) + (2 × 45)
2 × 90 = 90 + 90
2 × 90 = 180
By multiplying 2 with 90 we get 180
by adding 90 with 90 we get 180.
Question 9.
Use Structure Alyssa uses this area model to find the product 3 × 20. How can she use her drawing to find 3 × 40? Show your work.
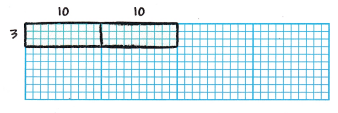
Answer:
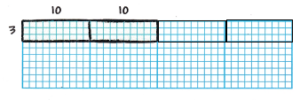
Question 10.
Gwyn places 9 rows of 80 tiles each on a table top. How many tiles does Gwyn place?

Answer:
Given,
Gwyn places 9 rows of 80 tiles each on a table top.
9 × 80 = 9 × (10 + 10 + 10 + 10 + 10 + 10 + 10 + 10)
= 720
Thus Gwyn place 720 tiles.
Question 11.
Geography The Arctic Circle marks the place at which the sun never sets during summer and the sun never rises during winter. The location of the Arctic Circle depends on Earth’s tilt. The pull of gravity from the moon increases this tilt, causing the Arctic Circle to move north about 50 feet each year. How far north will the Arctic Circle have moved after 7 years? Use the Distributive Property to find your answer.
Answer:
Given,
The Arctic Circle marks the place at which the sun never sets during summer and the sun never rises during winter.
The location of the Arctic Circle depends on Earth’s tilt.
The pull of gravity from the moon increases this tilt, causing the Arctic Circle to move north about 50 feet each year.
7 × 50 = (7 × 10) + (7 × 10) + (7 × 10) + (7 × 10) + (7 × 10)
7 × 50 = 70+ 70 + 70 + 70 + 70
7 × 50 = 350
Question 12.
Use Repeated Reasoning Michael says he knows four different ways to use the Distributive Property to find 7 × 40 as a product of a number and a sum of multiples of 10. Is he correct? If so, show four different ways to find 7 × 40. Is the product for each way the same? Explain.
Answer:
Method 1:
7 × 40 = 7 × (10 + 10 + 10 + 10)
7 × 40 = (7 × 10) + (7 × 10) + (7 × 10) + (7 × 10)
7 × 40 = 70 + 70 + 70 + 70
7 × 40 = 280
Method 2:
7 × 40 = 7 × (20 + 20)
7 × 40 = (7 × 20) + (7 × 20)
7 × 40 = 140 + 140
7 × 40 = 280
Method 3:
7 × 40 = 7 × (10 + 30)
7 × 40 = (7 × 10) + (7 × 30)
7 × 40 = 70 + 210
7 × 40 = 280
Method 4:
7 × 40 = 7 × (15+ 25)
7 × 40 = (7 × 15) + (7 × 25)
7 × 40 = 105 + 175
7 × 40 = 280
I’m in a Learning Mindset!
What helps me remember how to use the Distributive Property?