We included HMH Into Math Grade 3 Answer Key PDF Module 4 Lesson 7 Identify Number Patterns on the Multiplication Table to make students experts in learning maths.
HMH Into Math Grade 3 Module 4 Lesson 7 Answer Key Identify Number Patterns on the Multiplication Table
I Can identify arithmetic patterns in the multiplication table and explain them by using the properties of operations. I can use patterns and properties to find products in a table and to identify products as odd or even.
Spark Your Learning
Pens are sold in packs of 1, 2, 3, 4, 5, or 6 pens. Ray wants to buy an even number of pens. If Ray buys 3 packs of pens with the same number of pens in each pack, which packs would give him an even number of pens?

Show how you found your answer. Complete the products in the table. Write even or odd.
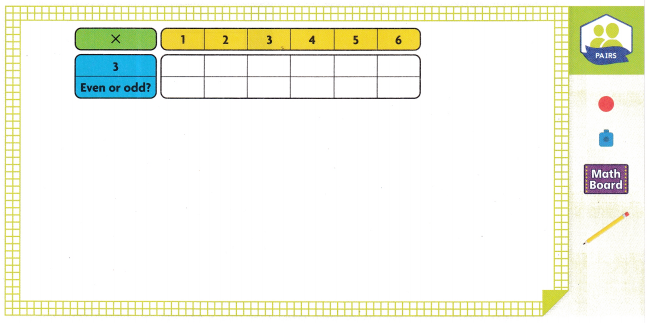
Answer:
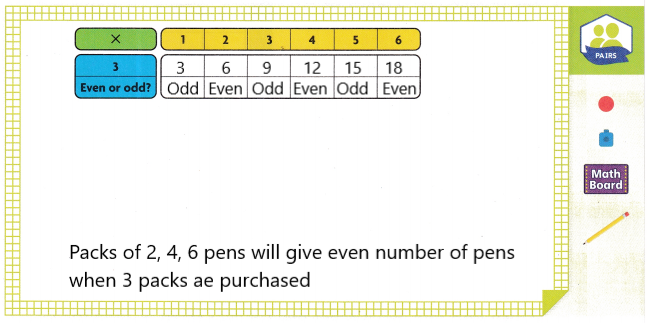
Explanation:
Pens are sold in packs of 1, 2, 3, 4, 5, or 6 pens. Ray wants to buy an even number of pens
If Ray buys 3 packs of pens with the same number of pens in each pack
Multiply the numbers 1 to 6 with 3
1 x 3 = 3 it is odd number
2 x 3 = 6 it is even number
3 x 3 = 9 it is odd number
4 x 3 = 12 it is even number
5 x 3 = 15 it is odd number
6 x 3 = 18 it is even number
So, if Ray buys 3 packs of 2, 4 or 6 pens she will get an even number of pens.
Turn and Talk Look for even and odd patterns in the factors and the products. What do you notice?
Answer:
An even number multiplied by any number will result in even number
An odd number multiplied by even number will result in even number and an odd number multiplied by odd number will result in an odd number.
Build Understanding
1. Nan is using patterns and multiplication properties to find products on a multiplication table.
A. Nan uses the Identity Property to find the products 1 × 2 and 5 × 1. Use the Identity Property to find other products.

B. Nan uses the Zero Property to find the products 8 × 0 and 0 × 9. Use the Zero Property to find other products.
C. Complete the columns for 3 and 4. Use the sum of the products for 3 and 4 to complete the products in the column for 7.
D. Nan uses the Commutative Property to find the products 8 × 2 and 2 × 8. Use the Commutative Property to find other products.
E. Describe any other patterns you can use to find products in the multiplication table.
Answer:

Any number multiplied with 0 will be always 0.
From the table see that all the numbers that are multiplied by 0 are 0.
Turn and Talk What other two columns could be used to help find the products in the column for 7? How does the Distributive Property explain this pattern?
Answer:
7 = 5 + 2
The other two columns that can be used to help find the products in the column for 7 is 5 and 2.
2. Jacy wants to use patterns and multiplication properties on the multiplication table to see if products are even or odd. How can you help him?

A. Choose an even factor as a first factor. Shade the row of products.
What even or odd pattern do you see in the products?
B. Choose a different first factor that is even. Shade the row of products.
What even or odd pattern do you see in the products?
C. Choose a column for a second factor that is odd. Shade the column of products.
What even or odd pattern do you see in the products?
____________________________
____________________________
____________________________
Answer:
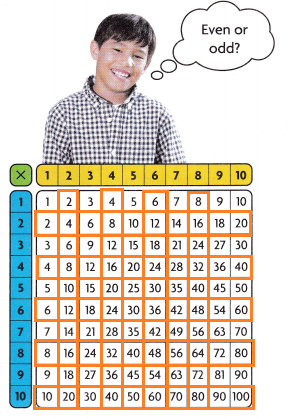
Let us take 2 as the first factor of even.
The row and column of factors of 2 are shaded in the below table.
We can observe that all the numbers are even.
Turn and Talk Suppose you choose a different second factor that is even and shade the column of products. Describe the even or odd pattern you see in the products.
Answer:
If you take 4 as the even factor then you can see the even patterns in the product.
Step It Out
3. Taya and Lew each think they may have found a pattern. Does each person’s statement make sense?

Use the arrays.
Taya’s Statement
even × odd = even
Try 4 × 7.
A. Break apart the array into 2 equal groups.

B. I broke apart the array into ___ and ___.
C. Are there equal groups with no tiles left over? ___
D. The product is ____.
Answer:
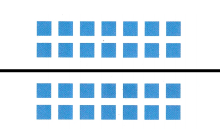
Explanation:
I broke apart the array into 14 and 14 tiles
The equal groups have no tiles left over
So, the product is Even.
Lew’s Statement
even × even = even
Try 2 × 8.
A. Circle equal groups.

B. I circled ___ pairs of ___ tiles each.
C. Are there equal groups with no tiles left over? ___
D. The product is ____
Does Taya’s statement make sense? ____
Does Lew’s statement make sense? ____
Answer:
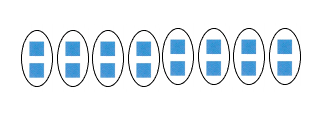
Explanation:
I circled 8 pairs of 2 tiles each
The equal groups have no tiles leftover
So, the product is even.
Therefore, both Taya’s and Lew’s statements make sense.
Check Understanding Math Board
Question 1.
Tarek is using the Identity Property of Multiplication to find 7 × 1 = 7. What is another multiplication fact you can find using the Identity Property?
Answer:
1 x 7 = 7 is another fact that Tarek can find using the Identity property of multiplication.
Is the product even or odd? Write even or odd.
Question 2.
3 × 3
Answer:
Odd
Explanation:
3 x 3 = 9
9 is not divisible by 2
So, 9 is odd number.
Question 3.
6 × 9
Answer:
Even
Explanation:
6 x 9 = 56
56 is divisible by 2
So, 56 is an even number.
Question 4.
2 × 8
Answer:
Even
Explanation:
2 x 8 = 16
16 is divisible by 2
So, 16 is an even number.
Question 5.
5 × 7
Answer:
Odd
Explanation:
5 x 7 = 35
35 is not divisible by 2
So, 35 is an odd number.
Question 6.
4 × 5
Answer:
Even
Explanation:
4 x 5 = 20
20 is divisible by 2
So, 20 is an even number.
On Your Own
Question 7.
Look for Repeated Reasoning Use the multiplication table. Complete the products in the column for the factor 6.
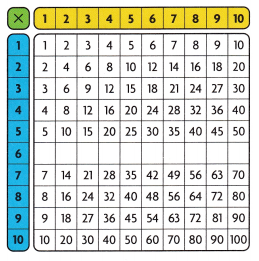
- What even or odd pattern do you see in the products?
Answer:
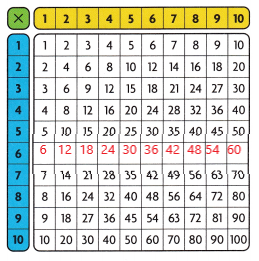
Explanation:
The product of 6’s fact with factors 1 to 10 are 6,12,18,24,30,36,42,48,54 and 60
All the products are divisible by 2
The numbers that are divisible by 2 are even numbers
So, i noticed an even number pattern in the row.
Question 8.
To find 6 × 4, how can you break apart the factor 4 into equal addends to find the product?
Answer:
6 x 4 = 24
Explanation:
I break factor 4 into two equal addends they are 2 and 2
Use 2’s fact with factor 6
2 x 6 = 12
Double the product
12 + 12 = 24
So, 6 x 4 = 24.
Write the unknown number.
Question 9.
9 × 6 = (4 + ___) × 6
Answer:
9 × 6 = (4 + 5) × 6
Explanation:
In distribute property we break apart 9
We already have 4
9 – 4 = 5
So, the unknown number is 5.
Question 10.
7 × 8 = 7 × (2 + __)
Answer:
7 × 8 = 7 × (2 + 6)
Explanation:
In distribute property we break apart 8
We already have 2
8 – 2 = 6
So, the unknown number is 6.
On Your Own
Question 11.
Use Structure Use the multiplication table. Complete the products in the column for the factor 7.
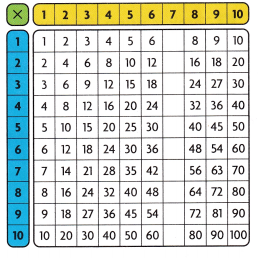
- What even or odd pattern do you see in the products?
Answer:
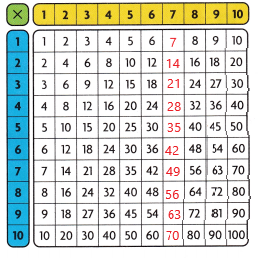
Explanation:
The product of 7’s fact with factors 1 to 10 are 7,14,21,28,35,42,49,56,63,70
In the products 7, 21, 35, 49, 63 are not divisible by 2
In the products 14, 28, 42, 56, 70 are divisible by 2
So, some the products are even and some are odd
The pattern the products follow is an odd number followed by an even number and again odd number and so on.
So, the pattern is odd, even, odd, even and so on.
Question 12.
Use Tools Describe how you would use the Commutative Property to find the product of two multiplication facts on the multiplication table.
Answer:
The commutative property is a math rule that says that the order in which we multiply numbers does not change the product.

8 × 2 = 2 × 8 = 16
The multiples in the above table will not be changed by changing the order of the product.
Is the product even or odd? Write even or odd.
Question 13.
1 × 4
Answer:
Even
Explanation:
1 x 4 = 4
4 is divisible by 2.
So, 4 is even number.
Question 14.
3 × 7
Answer:
Odd
Explanation:
3 x 7 = 21
21 is not divisible by 2
So, 21 is odd number.
Question 15.
6 × 6
Answer:
Even
Explanation:
6 x 6 = 36
36 is divisible by 2
So, it is even number.
Question 16.
7 × 8
Answer:
Even
Explanation:
7 x 8 = 56
56 is divisible by 2
So, 56 is even number.
Question 17.
9 × 9
Answer:
Odd
Explanation:
9 x 9 = 81
81 is not divisible by 2
So, 81 is odd number.
I’m in a Learning Mindset!
How do I know if I used an effective strategy to solve Problem 12?
________________________________