We included HMH Into Math Grade 3 Answer Key PDF Module 14 Lesson 2 Partition Shapes into Equal Areas to make students experts in learning maths.
HMH Into Math Grade 3 Module 14 Lesson 2 Answer Key Partition Shapes into Equal Areas
I Can divide shapes into parts with equal areas and write each equal part as a fraction.
Spark Your Learning
Mia designs a playground. She plans to divide it into 4 parts with equal areas. So far, Mia has found one way to divide the playground.

Show another way to divide the playground. Explain how you know that the 4 parts of your plan are equal in area.
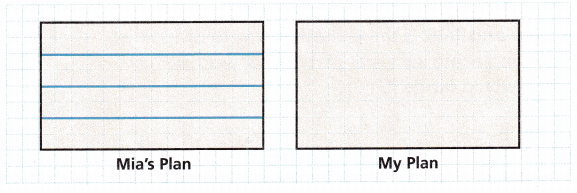
Answer:
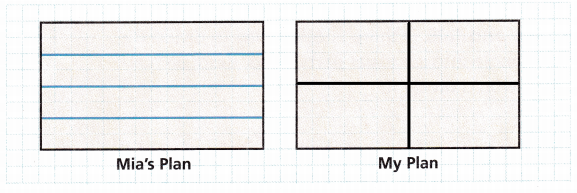
Explanation:
Mia designs a playground. She plans to divide it into 4 parts with equal areas
So far, Mia has found one way to divide the playground
I divided the play ground into four parts in another possible way
I divided the whole into 2 equal parts first and then each part into 2 equal halves again. So, i can say that all the 4 parts are equal.
Turn and Talk Can two rectangles be equal in area if they have different shapes? How do you know?
Answer:
Yes, two rectangles can be equal in area even if they have different shapes. even though the length of the rectangles differ the area it covers could be equal.
Build Understanding
Question 1.
How can you divide the rectangle into 6 parts with equal areas?

Answer:
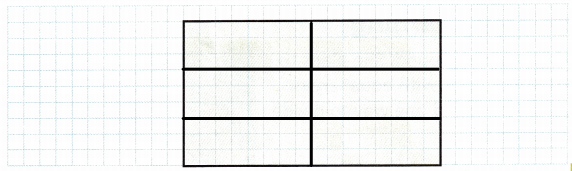
A. How do you know that the parts are equal in area?
Answer:
I divided the rectangle into equal parts
I divided the whole into 2 equal parts first and then each part into 3 equal parts again. So, i can say that all the 6 parts are equal.
B. What fraction of the whole rectangle is each part?
Answer:
\(\frac{1}{6}\)
Explanation:
There are 6 parts in the whole
The fraction of 1 part of the whole rectangle is \(\frac{1}{6}\).
Turn and Talk Is there another way to divide the rectangle into six equal parts? If so, describe how you would divide it.
Answer:
yes, we can divide the rectangle into 6 equal parts in other way by dividing it vertically into 6 smaller rectangles.
Question 2.
Divide the circle so that each part is \(\frac{1}{3}\) of the area of the whole shape. How can you show that each part of your circle is equal in area? Explain.

Answer:
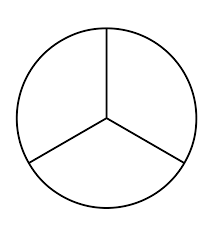
Explanation:
I divided the circle into 3 equal parts so that each part is \(\frac{1}{3}\) of the area of the whole shape.
Question 3.
Critique Reasoning Angela and Pedro divide rectangles into 8 equal parts in different ways. Both rectangles are the same size and shape.
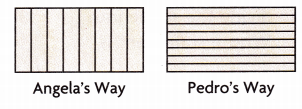
A. Do the parts from Angela’s rectangle have the same shape as the parts from Pedro’s rectangle? Explain.
Answer:
No, the parts of Angela’s rectangle does not have the same shape as the parts of Pedro’s rectangle as the parts of Angela’ s rectangle are made with vertically and the parts of Pedro’s rectangle are made horizontally.
B. Who divided the rectangle into parts that are greater in area, Angela or Pedro? Explain how you know.
Answer:
Both Angela or Pedro divided their rectangle into equal parts. So, the parts of both have same area.
Turn and Talk How can you show another way to divide the rectangle into 8 equal parts?
Answer:

explanation:
I drew a way to divide a rectangle into 8 parts other than the ways Angela and Pedro did.
Check Understanding
Question 1.
What fraction of the total area of the circle does each equal part represent?

Answer:
\(\frac{1}{4}\)
Explanation:
The circle is divided into 4 equal parts
So, each part represent \(\frac{1}{4}\) fraction of total area of circle.
Question 2.
Nora and Nick cut felt squares to make 6 equal-sized patches. Nick wants his patches to have a different shape but the same area as Nora’s patches. Draw lines to show how they can cut each of the felt squares.

Answer:

Explanation:
Nora and Nick cut felt squares to make 6 equal-sized patches. Nick wants his patches to have a different shape but the same area as Nora’s patches.
So, i drew lines to show how they can cut each of the felt squares in different ways
Now both of them have equal parts with different shapes.
On Your Own
Question 3.
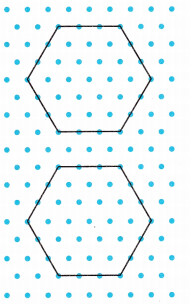
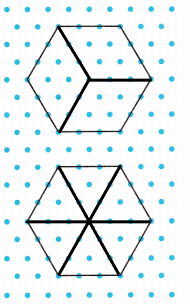
Construct Arguments Glenn says he can divide the six-sided shape into 3 parts with equal areas. Emily says she can divide the shape into 6 parts with equal areas. Whose statement is correct? Draw to explain.
Answer:
Explanation:
Glenn says he can divide the six-sided shape into 3 parts with equal areas.
Emily says she can divide the shape into 6 parts with equal areas
Both are correct, we can divide a six-sided shape into 3 as well as six equal parts as i drew above
The first shape represents shape with 3 equal parts and the second shape represents shape with 6 equal parts.
Question 4.
Attend to Precision Divide the shape into 6 equal parts.
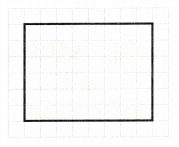
How do you know that you divided your shape into 6 equal parts?
Answer:
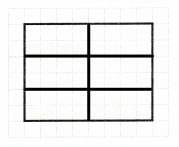
Explanation:
I divided the above given shape into 6 equal parts
I counted the number of boxes each part cover
All the parts cover same number of boxes in area grid
So, i know that i divided my shape into 6 equal parts.
Use the shapes for 5-6.
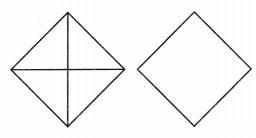
Question 5.
Shade \(\frac{1}{4}\) of the shape on the left.
Answer:
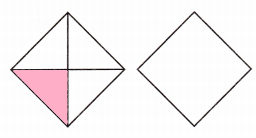
Explanation:
I shaded 1 part of shape in the left
The shaded part represents the fraction \(\frac{1}{4}\) .
Question 6.
Is there another way to divide the shape into 4 equal parts?
If yes, draw lines on the shape on the right to show a way. Shade the shape to show \(\frac{1}{4}\).
Answer:
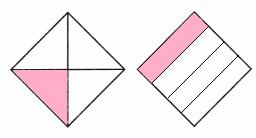
Explanation:
Yes, their is an another way to divide the given shape into 4 equal parts
I drew lines to divide, the right side shape is another way i have shown
I shaded 1 part of the 4 equal parts
I shaded the shape to show \(\frac{1}{4}\).
I’m in a Learning Mindset!
How can I use different tools and strategies to help me see if i have divided a shape into parts with equal areas?
Answer: