Free PDF Download links of Go Math Grade 4 Answer Key Homework Practice FL Chapter 6 Fraction Equivalence and Comparison are prevailing here for free. Simply refer to them once and make use of the Go Math Grade 4 Chapter 6 Fraction Equivalence and Comparison Answer Key Homework Practice FL to practice all questions covered in the Go Math Grade 4 Chapter 6 Textbook. The biggest goal of preparing these Answer Key Homework Practice FL by our team is to make students understand the concepts and secure well in the exams.
Go Math Grade 4 Answer Key Homework Practice FL Chapter 6 Fraction Equivalence and Comparison
Find all step-by-step explanations for every question from these Answer key of grade 4 HMH Go Math Ch 6 Homework Practice FL. Hence, take a look at the list of the toppers recommended HMH Go Math Grade 4 Solution Key for Chapter 6 Fraction Equivalence and Comparison and learn all the basics easily. In Chapter 6 go math HMH grade 4 Solution Key, you will find the topics like Equivalent Fractions, Comparing fractions, pair of fractions as a pair of fractions with a common denominator, and so on.
Lesson: 1 – Equivalent Fractions
- Common Core – Fraction Equivalence and Comparison – Page No. 113
- Common Core – Fraction Equivalence and Comparison – Page No. 114
Lesson: 2
- Common Core – Fraction Equivalence and Comparison – Page No. 115
- Common Core – Fraction Equivalence and Comparison – Page No. 116
Lesson: 3
- Common Core – Fraction Equivalence and Comparison – Page No. 117
- Common Core – Fraction Equivalence and Comparison – Page No. 118
Lesson: 4
- Common Core – Fraction Equivalence and Comparison – Page No. 119
- Common Core – Fraction Equivalence and Comparison – Page No. 120
Lesson: 5
- Common Core – Fraction Equivalence and Comparison – Page No. 121
- Common Core – Fraction Equivalence and Comparison – Page No. 122
Lesson: 6
- Common Core – Fraction Equivalence and Comparison – Page No. 123
- Common Core – Fraction Equivalence and Comparison – Page No. 124
Lesson: 7
- Common Core – Fraction Equivalence and Comparison – Page No. 125
- Common Core – Fraction Equivalence and Comparison – Page No. 126
Lesson: 8
- Common Core – Fraction Equivalence and Comparison – Page No. 127
- Common Core – Fraction Equivalence and Comparison – Page No. 128
Lesson: 9
- Common Core – Fraction Equivalence and Comparison – Page No. 129
- Common Core – Fraction Equivalence and Comparison – Page No. 130
Common Core – Fraction Equivalence and Comparison – Page No. 113
Equivalent Fractions
Use the model to write an equivalent fraction.
Question 1.

\(\frac{4}{6}=\frac{2}{3}\)
Explanation:
The first image has 4 parts shaded out of 6 parts. Divide 8/10 with 2. You will get 2/3. That means 2 parts are shaded out of 3 parts.
Question 2.
![]()
\(\frac{3}{4}\) = \(\frac{□}{□}\)
Answer: \(\frac{3}{4}\) = \(\frac{6}{8}\)
Explanation:
The first image has 3 parts shaded out of 4 parts. Multiply 8/10 with 2. You will get 6/8. That means 6 parts are shaded out of 8 parts.
Tell whether the fractions are equivalent. Write = or ≠.
Question 3.
\(\frac{8}{10}\) _____ \(\frac{4}{5}\)
Answer: \(\frac{8}{10}\) = \(\frac{4}{5}\)
Explanation:
Multiply the numerator and denominator of 4/5 with 2.
8/10 = (2/2) × (4/5)
= 8/10
So, 8/10 = 4/5.
Question 4.
\(\frac{1}{2}\) _____ \(\frac{7}{12}\)
Answer: \(\frac{1}{2}\) ≠ \(\frac{7}{12}\)
Explanation:
Multiply the numerator and denominator of 1/2 with 6
1/2 = (6/6) x (1/2)
= (6/12)
So, 1/2 ≠ 7/12
Question 5.
\(\frac{3}{4}\) _____ \(\frac{8}{12}\)
Answer: \(\frac{3}{4}\) ≠ \(\frac{8}{12}\)
Explanation:
Multiply the numerator and denominator of 3/4 with 3.
3/4 = (3/3) × (3/4)
= (9/12)
So, 3/4 ≠ 8/12
Question 6.
\(\frac{2}{3}\) _____ \(\frac{4}{6}\)
Answer: \(\frac{2}{3}\) = \(\frac{4}{6}\)
Explanation:
Multiply the numerator and denominator of 2/3 with 2.
2/3 = (2/2) × (2/3)
= 4/6
So, 2/3 = 4/6.
Question 7.
\(\frac{5}{8}\) _____ \(\frac{4}{10}\)
Answer: \(\frac{5}{8}\) ≠ \(\frac{4}{10}\)
Explanation:
Multiply the numerator and denominator of 5/8 with 2
5 / 8 =(2/2) x (5/ 8)
= (10/16)
So, 5/8 ≠ 4/10
Question 8.
\(\frac{2}{6}\) _____ \(\frac{4}{12}\)
Answer:
Question 9.
\(\frac{20}{100}\) _____ \(\frac{1}{5}\)
Answer: \(\frac{20}{100}\) = \(\frac{1}{5}\)
Explanation:
Cross Multiply the 20/100 with 20/20
20/100 = (20/20) x (20/100)
= (1/5)
So, 20/100 = 1/5.
Question 10.
\(\frac{5}{8}\) _____ \(\frac{9}{10}\)
Answer: \(\frac{5}{8}\) ≠ \(\frac{9}{10}\)
Explanation:
Multiply the numerator and denominator of 5/8 with 2
5/8 = (2/2) x (5/8)
= 10/16
So, 5/8 ≠ 9/10
Question 11.
Jamal finished \(\frac{5}{6}\) of his homework. Margaret finished \(\frac{3}{4}\) of her homework, and Steve finished \(\frac{10}{12}\) of his homework. Which two students finished the same amount of homework?
_________
Answer: Jamal and Steve
Explanation:
As per the given data,
Jamal finished work = 5 /6 of his homework
Margaret finished work = 3 /4th of her homework
Steve finished work = 10/12 of his homework
Multiply the numerator and denominator of 5/6 with 2
Then, (2/2) x (5/6) = 10/12
Then, Jamal and Steve finished the same amount of homework.
Question 12.
Sophia’s vegetable garden is divided into 12 equal sections. She plants carrots in 8 of the sections. Write two fractions that are equivalent to the part of Sophia’s garden that is planted with carrots.
Type below:
_________
Answer: 2/3 and 4/6
Explanation:
As per the given data,
Sophia’s vegetable garden is divided into 12 equal sections
She plants carrots in 8 of the sections out of 12 sections = 8/12
By simplifying the 8/12, we will get 4/6
Again simplify the 4 /6 by dividing method, you will get 2 /3
2/3 = (2/2) x (2/3)
= 4/6
Then, the equivalent fractions are 2/3, 4 /6
Common Core – Fraction Equivalence and Comparison – Page No. 114
Question 1.
A rectangle is divided into 8 equal parts. Two parts are shaded. Which fraction is equivalent to the shaded area of the rectangle?
Options:
a. \(\frac{1}{4}\)
b. \(\frac{1}{3}\)
c. \(\frac{2}{6}\)
d. \(\frac{3}{4}\)
Answer: \(\frac{1}{4}\)
Explanation:
As per the given data,
A rectangle is divided into 8 equal parts
Two parts are shaded
Then, the shaded area of rectangle = 2/8
By simplifying the 2/8, you will get 1/4
So, the shaded area of rectangle = 1/4
Thus the correct answer is option a.
Question 2.
Jeff uses 3 fifth-size strips to model \(\frac{3}{5}\). He wants to use tenth-size strips to model an equivalent fraction. How many tenth-size strips will he need?
Options:
a. 10
b. 6
c. 5
d. 3
Answer: 6
Explanation:
From the given data,
Jeff uses 3 fifth –size strips to model = 3 / 5 size strips
If he wants to use tenth – size strips to an equivalent fraction = 1 / 10 size strips
The number of strips = x
(1/10) x = 3/5
x = 30/5
then, the required number of tenth size trips = 6
Thus the correct answer is option b.
Question 3.
Cassidy places 40 stamps on each of 8 album pages. How many stamps does she place in all?
Options:
a. 300
b. 320
c. 360
d. 380
Answer: 320
Explanation:
As per the given data,
Cassidy places 40 stamps on each of 8 album pages = 8 x 40 = 320
So, totally placed stamps on album pages by Cassidy = 320 stamps
Thus the correct answer is option b.
Question 4.
Maria and 3 friends have 1,200 soccer cards. If they share the soccer cards equally, how many will each person receive?
Options:
a. 30
b. 40
c. 300
d. 400
Answer: 300
Explanation:
As per the given data,
Maria and 3 friends have 1200 soccer cards
If soccer cards shared equally by four members = 1200/4 = 300
Then, each person received soccer cards = 300
Thus the correct answer is option c.
Question 5.
Six groups of students sell 162 balloons at the school carnival. There are 3 students in each group. If each student sells the same number of balloons, how many balloons does each student sell?
Options:
a. 9
b. 18
c. 27
d. 54
Answer: 9
Explanation:
As per the given, data,
Six groups of students sell 162 balloons at the school carnival
There are 3 students in each group
Then, total number of students in 6 groups = 6 x 3 = 18
If each student sells the same number of balloons = 162 / 18 = 9
Number of balloons sells by each student = 9
Thus the correct answer is option a.
Question 6.
Four students each made a list of prime numbers.
Eric: 5, 7, 17, 23
Maya: 3, 5, 13, 17
Bella: 2, 3, 17, 19
Jordan: 7, 11, 13, 21
Who made an error and included a composite number?
Options:
a. Eric
b. Maya
c. Bella
d. Jordan
Answer: Jordan
Explanation:
As per the given data,
Four students each made a list of prime numbers.
Eric: 5, 7, 17, 23
Maya: 3, 5, 13, 17
Bella: 2, 3, 17, 19
Jordan: 7, 11, 13, 21
21 is not a prime number.
So, An error made by Jordan.
Thus the correct answer is option d.
Common Core – Fraction Equivalence and Comparison – Page No. 115
Write two equivalent fractions for each.
Question 1.
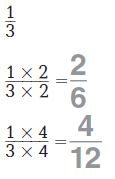
Question 2.
\(\frac{2}{3}\)
Type below:
_________
Answer: 4/6 and 8/12
Explanation:
2/3
(2/3) x (2/2) = 4/6
(2/3) x (4/4) = 8/12
Then, the equivalent fractions of 2/3 = 4/6 and 8/12
Question 3.
\(\frac{1}{2}\)
Type below:
_________
Answer: 2/4 and 4/8
Explanation:
1/2
(1/2) x (2/2) = 2/4
(1/2) x (4/4) = 4/8
Then, the equivalent fractions of 1/2 = 2/4, 4/8
Question 4.
\(\frac{4}{5}\)
Type below:
_________
Answer: 8/10 and 80/100
Explanation:
4/5
(4/5) x (2/2) = 8/10
(4/5) x (20/20) = 80/100
Then, the equivalent fractions of 4/5 = 8/10 and 80/100
Tell whether the fractions are equivalent. Write # or ≠.
Question 5.
\(\frac{1}{4}\) _____ \(\frac{3}{12}\)
Answer: \(\frac{1}{4}\) = \(\frac{3}{12}\)
Explanation:
1/4
Multiply the numerator and denominator of 1/4 with 3
Then, (1/4) x (3/3) = 3/12
So, 1/4 = 3/12
Question 6.
\(\frac{4}{5}\) _____ \(\frac{5}{10}\)
Answer: \(\frac{4}{5}\) ≠ \(\frac{5}{10}\)
Explanation:
4/5
Multiply numerator and denominator of 4/5 with 2
(4/5) x (2/2) = 8/10
Then 4/5 ≠ 5/10
Question 7.
\(\frac{3}{8}\) _____ \(\frac{2}{6}\)
Answer: \(\frac{3}{8}\) ≠ \(\frac{2}{6}\)
Explanation:
3/8 ≠ 2/6
Question 8.
\(\frac{3}{4}\) _____ \(\frac{6}{8}\)
Answer: \(\frac{3}{4}\) = \(\frac{6}{8}\)
Explanation:
3/4
Multiply the numerator and denominator of 3/4 with 2
Then, (3/4) x (2/2) = 6/8
So, 3/4 = 6/8
Question 9.
\(\frac{5}{6}\) _____ \(\frac{10}{12}\)
Answer: \(\frac{5}{6}\) = \(\frac{10}{12}\)
Explanation:
5/6
Multiply the numerator and denominator with 2
(5/6) x (2/2) = 10/12
So, 5/6 = 10/12
Question 10.
\(\frac{6}{12}\) _____ \(\frac{5}{8}\)
Answer: \(\frac{6}{12}\) ≠ \(\frac{5}{8}\)
Explanation:
6/12 ≠ 5/8
Question 11.
\(\frac{2}{5}\) _____ \(\frac{4}{10}\)
Answer: \(\frac{2}{5}\) = \(\frac{4}{10}\)
Explanation:
2/5
Multiply the numerator and denominator of 2/5 with 2
(2/5) x (2/2) = 4/10
So, 2/5 = 4/10
Question 12.
\(\frac{2}{4}\) _____ \(\frac{3}{12}\)
Answer: \(\frac{2}{4}\) ≠ \(\frac{3}{12}\)
Explanation:
2/4
Multiply the numerator and denominator of 2/4 with 3
(2/4) x (3/3) = 6/12
So, 2/4 ≠ 3/ 12
Question 13.
Jan has a 12-ounce milkshake. Four ounces in the milkshake are vanilla, and the rest is chocolate. What are two equivalent fractions that represent the fraction of the milkshake that is vanilla?
Type below:
_________
Answer: 1/3 and 2/6
Explanation:
As per the given data,
Jan has a 12-ounce milkshake
Four ounces in the milkshake are vanilla = 4/12 = 1/3
Then, 8-ounces in milkshake are chocolate = 8/12 = 2/3
4/12 = 1/3
By multiplying 1/3 with 2
(1/3) x (2/2) = 2/6
So, the equivalent fractions of vanilla milkshake are 1/3 and 2/6.
Question 14.
Kareem lives \(\frac{4}{10}\) of a mile from the mall. Write two equivalent fractions that show what fraction of a mile Kareem lives from the mall.
Type below:
_________
Answer: 2/5 and 8/20
Explanation:
As per the given data,
Kareem lives 4/10 of a mile from the mall
To find the equivalent fractions of 4/10
Simplify the 4/10 = 2/5
Multiply the numerator and denominator of 2/5 with 4
(2/5) x (4/4) = 8/20
Then, the equivalent fraction of a mile Kareem lives from the mall = 2/5 and 8/20
Common Core – Fraction Equivalence and Comparison – Page No. 116
Question 1.
Jessie colored a poster. She colored \(\frac{2}{5}\) of the poster red. Which fraction is equivalent to \(\frac{2}{5}\) ?
Options:
a. \(\frac{4}{10}\)
b. \(\frac{7}{10}\)
c. \(\frac{4}{5}\)
d. \(\frac{2}{2}\)
Answer: \(\frac{4}{10}\)
Explanation:
As per the given data,
Jessie colored a poster
She colored 2/5th of the poster red
Multiply the numerator and denominator of 2/5 with 2
Then, (2/5) x (2/2) = 4 /10
So, the equivalent fraction of 2/5 is 4/10.
Thus the correct answer is option a.
Question 2.
Jessie colored a poster. She colored \(\frac{1}{4}\) of the poster red. Which fraction is equivalent to \(\frac{1}{4}\) ?
Options:
a. \(\frac{2}{5}, \frac{3}{12}\)
b. \(\frac{2}{8}, \frac{4}{12}\)
c. \(\frac{3}{4}, \frac{6}{8}\)
d. \(\frac{2}{8}, \frac{3}{12}\)
Answer: \(\frac{2}{8}, \frac{3}{12}\)
Explanation:
As per the given data,
Marcus makes a punch that is 1/4th of cranberry juice
Multiply the numerator and denominator of 1/4 with 2
Then, (1/4) x (2/2) = 2/8
Multiply the numerator and denominator of 1/4 with 3
Then, (1/4) x (3/3) = 3/12
Equivalent fractions of 1/4 are 2/8 and 3/12.
Thus the correct answer is option d.
Question 3.
An electronics store sells a large flat screen television for $1,699. Last month, the store sold 8 of these television sets. About how much money did the store make on the television sets?
Options:
a. $160,000
b. $16,000
c. $8,000
d. $1,600
Answer: $16,000
Explanation:
As per the given data,
An electronics store sells a large flat-screen television for $1,699
Last month, the store sold 8 of these television sets = 8 x $1,699 = $13,952. The money is about to $16,000.
Thus the correct answer is option b.
Question 4.
Matthew has 18 sets of baseball cards. Each set has 12 cards. About how many baseball cards does Matthew have in all?
Options:
a. 300
b. 200
c. 150
d. 100
Answer: 200
Explanation:
From the given data,
Matthew has 18 sets of basketball cards
Each set has 12 cards = 12 x 18 = 216
Total number of basketball cards with Matthew = 216.
So, it is near to 200.
Thus the correct answer is option b.
Question 5.
Diana had 41 stickers. She put them in 7 equal groups. She put as many as possible in each group. She gave the leftover stickers to her sister. How many stickers did Diana give to her sister?
Options:
a. 3
b. 4
c. 5
d. 6
Answer: 6
Explanation:
As per the given data,
Diana has 41 stickers
She put them in 7 equal groups = 41/7
= 5 (remaining 6)
She gave the leftover stickers to her sister
The number of stickers Diana give to her sister = 6
Thus the correct answer is option d.
Question 6.
Christopher wrote the number pattern below. The first term is 8.
8, 6, 9, 7, 10, …
Which is a rule for the pattern?
Options:
a. Add 2, add 3.
b. Add 6, subtract 3.
c. Subtract 6, add 3.
d. Subtract 2, add 3
Answer: Subtract 2, add 3
Explanation:
From the given data,
Christopher wrote the number pattern = 8, 6, 9, 7, 10, …..
The first number in the pattern = 8
8 – 2 = 6 + 3 = 9 – 2 = 7 +3 = 10 ….
So, the rule for the above pattern is to subtract 2, add 3.
Thus the correct answer is option d.
Common Core – Fraction Equivalence and Comparison – Page No. 117
Write the fraction in simplest form.
Question 1.
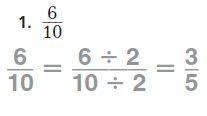
Explanation:
To write the 6/10 in a simplest form
Divide the numerator and denominator of 6/10 with 2
(6 ÷2)/(10 ÷2) = 3/5
So, the simplest form of 6/10 = 3/5
Question 2.
\(\frac{6}{8}\) = \(\frac{□}{□}\)
Answer: \(\frac{3}{4}\)
Explanation:
To write the 6/8in a simplest form
Divide the numerator and denominator of 6/8 with 2
(6 ÷2)/(8 ÷2) = 3/4
So, the simplest form of 6/8 = 3/4
Question 3.
\(\frac{5}{5}\) = \(\frac{□}{□}\)
Answer: \(\frac{1}{1}\)
Explanation:
To write the 5/5in a simplest form
Divide the numerator and denominator of 5/5 with 5
(5 ÷5)/(5 ÷5) = 1/1
So, the simplest form of 5/5 = 1
Question 4.
\(\frac{8}{12}\) = \(\frac{□}{□}\)
Answer: \(\frac{2}{3}\)
Explanation:
To write the 8/12in a simplest form
Divide the numerator and denominator of 8/12 with 4
(8 ÷4)/(12 ÷4) = 2/3
So, the simplest form of 8/12 = 2/3
Question 5.
\(\frac{100}{100}\) = \(\frac{□}{□}\)
Answer: 1
Explanation:
Any number divided by the same number will be always equal to 1.
The simplest form of 100/100 = 1
Question 6.
\(\frac{2}{6}\) = \(\frac{□}{□}\)
Answer: \(\frac{1}{3}\)
Explanation:
To write the 2/6in a simplest form
Divide the numerator and denominator of 2/6 with 2
(2 ÷2)/(6 ÷2) = 1/3
So, the simplest form of 2/6 = 1/3
Question 7.
\(\frac{2}{8}\) = \(\frac{□}{□}\)
Answer: \(\frac{1}{4}\)
Explanation:
To write the 2/8in a simplest form
Divide the numerator and denominator of 2/8 with 2
(2 ÷2)/(8 ÷2) = 1/4
So, the simplest form of 2/8 = 1/4
Question 8.
\(\frac{4}{10}\) = \(\frac{□}{□}\)
Answer: \(\frac{2}{5}\)
Explanation:
To write the 4/10 in a simplest form
Divide the numerator and denominator of 4 /10 with 2
(4 ÷2)/(10 ÷2) = 2/5
So, the simplest form of 4/10 = 2/5
Tell whether the fractions are equivalent. Write = or ≠. (if you dont have ≠on your keyboard, copy and paste this one: ≠ )
Question 9.
\(\frac{6}{12}\) ______ \(\frac{1}{12}\)
Answer: \(\frac{6}{12}\) ≠ \(\frac{1}{12}\)
Explanation:
6/12 ≠ 1/12
Question 10.
\(\frac{3}{4}\) ______ \(\frac{5}{6}\)
Answer: \(\frac{3}{4}\) ≠ \(\frac{5}{6}\)
Explanation:
3/4 ≠ 5/6
Question 11.
\(\frac{6}{10}\) ______ \(\frac{3}{5}\)
Answer: \(\frac{6}{10}\) = \(\frac{3}{5}\)
Explanation:
6/10
Divide the numerator and denominator of 6/10 with 2
(6 ÷ 2)/( 10 ÷ 2) = 3/5
So, 6/10 = 3/5
Question 12.
\(\frac{3}{12}\) ______ \(\frac{1}{3}\)
Answer: \(\frac{3}{12}\) ≠ \(\frac{1}{3}\)
Explanation:
3/12 ≠ 1/3
Question 13.
\(\frac{6}{10}\) ______ \(\frac{60}{100}\)
Answer: \(\frac{6}{10}\) = \(\frac{60}{100}\)
Explanation:
6/10
Multiply the numerator and denominator of 6/10 with 10
(6 x 10)/(10 x 10) = 60/100
So, 6/10 = 60/100
Question 14.
\(\frac{11}{12}\) ______ \(\frac{9}{10}\)
Answer: \(\frac{11}{12}\) ≠ \(\frac{9}{10}\)
Explanation:
11/12 ≠ 9/10
Question 15.
\(\frac{2}{5}\) ______ \(\frac{8}{20}\)
Answer: \(\frac{2}{5}\) = \(\frac{8}{20}\)
Explanation:
2/5
Multiply the numerator and denominator of 2/5 with 4
(2 x 4)/(5 x 4) = 8/20
So, 2/5 = 8/20
Question 16.
\(\frac{4}{8}\) ______ \(\frac{1}{2}\)
Answer: \(\frac{4}{8}\) = \(\frac{1}{2}\)
Explanation:
4/8
Divide the numerator and denominator of 4/8 with 4
(4 x 4)/(8 x 4) = 1/2
So, 4/8 = 1/2
Question 17.
At Memorial Hospital, 9 of the 12 babies born on Tuesday were boys. In simplest form, what fraction of the babies born on Tuesday were boys?
\(\frac{□}{□}\)
Answer: \(\frac{3}{4}\)
Explanation:
As per the given data,
At the memorial hospital, 9 of the 12 babies born on Tuesday were boys = 9/12
Divide the numerator and denominator of 9/12 with 3
(9 ÷ 3)/(12 ÷ 3) = 3/4
So, in the simplest form
3/4 of the babies born on Tuesday were boys.
Question 18.
Cristina uses a ruler to measure the length of her math textbook. She says that the book is \(\frac{4}{10}\) meter long. Is her measurement in simplest form? If not, what is the length of the book in simplest form?
\(\frac{□}{□}\)
Answer: \(\frac{2}{5}\)
Explanation:
As per the given data,
Cristiana uses a ruler to measure the length of her math textbook
She says that the book is 4/10meter long
It is not in the simplest form
Divide the numerator and denominator of 4/10 with 2
(4÷ 2)/( 10 ÷ 2) = 2/5
The length of the book in the simplest form = 2/5.
Common Core – Fraction Equivalence and Comparison – Page No. 118
Question 1.
Six out of the 12 members of the school choir are boys. In simplest form, what fraction of the choir is boys?
Options:
a. \(\frac{1}{6}\)
b. \(\frac{6}{12}\)
c. \(\frac{1}{2}\)
d. \(\frac{12}{6}\)
Answer: \(\frac{1}{2}\)
Explanation:
As per the given data,
Six out of the 12 members of the school choir are boys = 6/12
To write the simplest form of 6/12, divide the numerator and denominator with 6
Then, (6 ÷ 6)/(12 ÷ 6) = 1/2
In the simplest form, 1/2 of the choir is boys.
Thus the correct answer is option c.
Question 2.
Six out of the 12 members of the school choir are boys. In simplest form, what fraction of the choir is boys?
Options:
a. \(\frac{5}{6}\)
b. \(\frac{6}{8}\)
c. \(\frac{8}{10}\)
d. \(\frac{2}{12}\)
Answer: \(\frac{5}{6}\)
Explanation:
5/6 is in the simplest form
6/8 simplest form = 3/4
8/10 simplest form = 4/5
2/12 simplest form = 1/6
Thus the correct answer is option a.
Question 3.
Each of the 23 students in Ms. Evans’ class raised $45 for the school by selling coupon books. How much money did the class raise in all?
Options:
a. $207
b. $225
c. $1,025
d. $1,035
Answer: $1,035
Explanation:
As per the given data,
Each of the 23 students in Ms. Evan’s class raised $45 for the school by selling coupon books
= 23 x $45
= $1,035
Thus the correct answer is option d.
Question 4.
Which pair of numbers below have 4 and 6 as common factors?
Options:
a. 12, 18
b. 20, 24
c. 28, 30
d. 36, 48
Answer: 36, 48
Explanation:
36, 48
Here, 36 = 4 x 9
= 2 x 2 x 3 x 3
48 = 6 x 8
= 2 x 3 x 4 x 2
Thus the correct answer is option d.
Question 5.
Bart uses \(\frac{3}{12}\) cup milk to make muffins. Which fraction is equivalent to \(\frac{3}{12}\) ?
Options:
a. \(\frac{1}{4}\)
b. \(\frac{1}{3}\)
c. \(\frac{1}{2}\)
d. \(\frac{2}{3}\)
Answer: \(\frac{1}{4}\)
Explanation:
As per the given data,
Bart uses 3/12 cup milk to make muffins
Divide the fraction with 3
(3 ÷ 3)/(12 ÷ 3) = 1/4
So, the equivalent fraction for 3/12 = 1/4
Thus the correct answer is option a.
Question 6.
Ashley bought 4 packages of juice boxes. There are 6 juice boxes in each package. She gave 2 juice boxes to each of 3 friends. How many juice boxes does Ashley have left?
Options:
a. 24
b. 22
c. 18
d. 12
Answer: 18
Explanation:
As per the given data,
Ashley bought 4 packages of juice boxes
There are 6 juice boxes in each package = 6 x 4 = 24
She gave 2 juice boxes to each of 3 friends = 2 x 3 = 6 juice boxes
So, 24 – 6 = 18
Total number of juice boxes left with Ashley = 18
Thus the correct answer is option c.
Common Core – Fraction Equivalence and Comparison – Page No. 119
Write the pair of fractions as a pair of fractions with a common denominator.
Question 1.
\(\frac{2}{3} \text { and } \frac{3}{4}\)
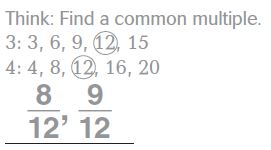
Explanation:
2/3 and 3/4
List the multiples of 3 = 3, 6, 9, 12, 15, 18, 21, 24, …
List the multiples of 4 = 4, 8, 12, 16, 20, …
Common multiple of 3 and 4 is 12
For the Common pair of fractions, multiply the common denominator with fractions
That is, (2 x 12) ÷( 3 x 12) and ( 3 x 12 ) ÷ ( 4 x 12)
So, common pair of fractions = 8/12 and 9/12
Question 2.
\(\frac{1}{4} \text { and } \frac{2}{3}\)
Type below:
_________
Answer: 3/4 and 8/12
Explanation:
1/4 and 2/3
List the multiples of 4 = 4, 8, 12, 16, 20, …
List the multiples of 3 = 3, 6, 9, 12, 15, 18, …
Common multiple of 4 and 3 is 12
For the Common pair of fractions, multiply the common denominator with fractions
That is, (1 x 12) ÷( 4 x 12) and ( 2 x 12 ) ÷ ( 3 x 12)
So, common pair of fractions = 3/12 and 8/12
Question 3.
\(\frac{3}{10} \text { and } \frac{1}{2}\)
Type below:
_________
Answer: 3/10 and 5/10
Explanation:
3/10 and 1/2
List the multiples of 10 = 10, 20, 30, 40, 50, ….
List the multiples of 2 = 2, 4, 6, 8, 10, 12, 14, ….
Common multiple of 10 and 2 is 10
For the Common pair of fractions, multiply the common denominator with fractions
That is, (3 x 10) ÷( 10 x 10) and ( 1 x 10 ) ÷ ( 2 x 10)
So, common pair of fractions = 3/10 and 5/10
Question 4.
\(\frac{3}{5} \text { and } \frac{3}{4}\)
Type below:
_________
Answer: 12/20 and 15/20
Explanation:
3/5 and 3/4
List the multiples of 5 = 5, 10, 15, 20, 25, 30, ….
List the multiples of 4 = 4, 8, 12, 16, 20, 24, …
Common multiple of 5 and 4 is 20
For the Common pair of fractions, multiply the common denominator with fractions
That is, (3 x 20) ÷( 5 x 20) and ( 3 x 20 ) ÷ ( 4 x 20)
So, common pair of fractions = 12/20 and 15/20
Question 5.
\(\frac{2}{4} \text { and } \frac{7}{8}\)
Type below:
_________
Answer: 4/8 and 7/8
Explanation:
2/4 and 7/8
List the multiples of 4 = 4, 8, 12, 16, 20, 24, …
List the multiples of 8 = 8, 16, 24, 32, 40, ….
Common multiple of 4 and 8 is 8
For the Common pair of fractions, multiply the common denominator with fractions
That is, (2 x 8) ÷( 4 x 8) and ( 7 x 8 ) ÷ ( 8 x 8)
So, common pair of fractions = 4/8 and 7/8
Question 6.
\(\frac{2}{3} \text { and } \frac{5}{12}\)
Type below:
_________
Answer: 8/12 and 5/12
Explanation:
2/3 and 5/12
List the multiples of 3 = 3, 6, 9, 12, 15, 18, …
List the multiples of 12 = 12, 24, 36, 48, 60, …
Common multiple of 3 and 12 is 12
For the Common pair of fractions, multiply the common denominator with fractions
That is, (2 x 12) ÷( 3 x 12) and ( 5 x 12 ) ÷ ( 12 x 12)
So, common pair of fractions = 8/12 and 5/12
Question 7.
\(\frac{1}{4} \text { and } \frac{1}{6}\)
Type below:
_________
Answer: 3/12 and 2/12
Explanation:
1/4 and 1/6
List the multiples of 4 = 4, 8, 12, 16, 20, 24, …
List the multiples of 6 = 6, 12, 18, 24, 30, …
Common multiple of 4 and 6 is 12
For the Common pair of fractions, multiply the common denominator with fractions
That is, (1 x 12) ÷( 4 x 12) and ( 1 x 12 ) ÷ ( 6 x 12)
So, common pair of fractions = 3/12 and 2/12.
Tell whether the fractions are equivalent. Write = or ≠.
Question 8.
\(\frac{1}{2}\) ______ \(\frac{2}{5}\)
Answer: \(\frac{1}{2}\) ≠ \(\frac{2}{5}\)
Explanation:
Multiply the numerator and denominator of 1/2 with 2
(1 x 2) ÷ (2 x 2) = 2/4
So, 1/2 ≠ 2/5
Question 9.
\(\frac{1}{2}\) ______ \(\frac{3}{6}\)
Answer: \(\frac{1}{2}\) = \(\frac{3}{6}\)
Explanation:
1/2
Multiply the numerator and denominator of 1/2 with 3
(1 x 3) ÷ (2 x 3) = 3/6
So, 1/2 = 3/6
Question 10.
\(\frac{3}{4}\) ______ \(\frac{5}{6}\)
Answer: \(\frac{3}{4}\) ≠ \(\frac{5}{6}\)
Explanation:
3/4 ≠ 5/6
Question 11.
\(\frac{6}{10}\) ______ \(\frac{3}{5}\)
Answer: \(\frac{6}{10}\) = \(\frac{3}{5}\)
Explanation:
6/10
Divide the numerator and denominator of 6/10 with 2
(6 ÷ 2)/(10 ÷2) = 3/5
So, 6/10 = 3/5
Question 12.
\(\frac{6}{8}\) ______ \(\frac{3}{4}\)
Answer: \(\frac{6}{8}\) = \(\frac{3}{4}\)
Explanation:
6/8
Divide the numerator and denominator of 6/8 with 2
(6 ÷2)/(8 ÷2) = 3/4
So, 6/8 = 3/4
Question 13.
\(\frac{3}{4}\) ______ \(\frac{2}{3}\)
Answer: \(\frac{3}{4}\) ≠ \(\frac{2}{3}\)
Explanation:
3/4 ≠ 2/3
Question 14.
\(\frac{2}{10}\) ______ \(\frac{4}{5}\)
Answer: \(\frac{2}{10}\) ≠ \(\frac{4}{5}\)
Explanation:
2/10
Divide the numerator and denominator of 2/10 with 8
(8 ÷ 2)/(10 ÷ 2) = 4/5
So, 2/10 ≠ 4/5
Question 15.
\(\frac{1}{4}\) ______ \(\frac{3}{12}\)
Answer: \(\frac{1}{4}\) = \(\frac{3}{12}\)
Explanation:
1/4
Multiply the numerator and denominator of 1/4 with 3
(1 x 3)/(4 x 3) = 3/12
So, 1/4 = 3/12
Question 16.
Adam drew two same size rectangles and divided them into the same number of equal parts. He shaded \(\frac{1}{3}\) of one rectangle and \(\frac{1}{4}\) of other rectangle. What is the least number of parts into which both rectangles could be divided?
_________
Answer: 12 parts
Explanation:
As per the given data,
Adam drew two same size rectangles and divided them into the same number of equal parts
He shaded 1/3 of one rectangle
1/4 of another rectangle
List the multiples of 3 = 3, 6, 9, 12, 15, 18, …
List the multiples of 4 = 4, 8, 12, 16, 20, …
A common multiple of 3 and 4 is 12
So, the least number of parts which rectangles could be divided = 12 parts
Question 17.
Mera painted equal sections of her bedroom wall to make a pattern. She painted \(\frac{2}{5}\) of the wall white and \(\frac{1}{2}\) of the wall lavender. Write an equivalent fraction for each using a common denominator.
Type below:
_________
Answer: 1/2 are 4/10 and 5/10
Explanation:
As per the given data,
Mera painted equal sections of her bedroom wall to make a pattern
She painted 2/5 of the wall white and 1/2 of the wall lavender
List the multiples of 5 = 5, 10, 15, 20, 25, 30, …
List the multiples of 2 = 2 ,4, 6, 8, 10, 12, 14, …
The common denominator of 2/5 and 1/2 = 10
Multiply the 2/5 and 1/2 with 10
(2 x 10)/(5 x 10) and (1 x 10)/(2 x 10)
4/10 and 5/10
So, common fractions of 2/5 and 1/2 are 4/10 and 5/10.
Common Core – Fraction Equivalence and Comparison – Page No. 120
Question 1.
Which of the following is a common denominator of \(\frac{1}{4}\) and \(\frac{5}{6}\) ?
Options:
a. 8
b. 9
c. 12
d. 15
Answer: 12
Explanation:
The common denominator of 1/4 and 5/6
List the multiples of 4 = 4, 8, 12, 16, 20, 24, …
List the multiples of 6 = 6, 12, 18, 24, 30, ….
So, the common denominator of 1/4 and 5/6 is 12
The correct answer is option c.
Question 2.
Two fractions have a common denominator of 8. Which of the following could be the two fractions?
Options:
a. \(\frac{1}{2} \text { and } \frac{2}{3}\)
b. \(\frac{1}{4} \text { and } \frac{1}{2}\)
c. \(\frac{3}{4} \text { and } \frac{1}{6}\)
d. \(\frac{1}{2} \text { and } \frac{4}{5}\)
Answer: \(\frac{1}{4} \text { and } \frac{1}{2}\)
Explanation:
As per the given data,
Two fractions have a common denominator of 8
a. 1/2 and 2/3
List the multiples of 2 = 2, 4, 6, 8,10, ….
List the multiples of 3 = 3, 6, 9, 12, …
There is no common denominator of 8 for 1/2 and 2/3
b. 1/4 and 1 /2
List the multiples of 2 = 2, 4, 6, 8,10, ….
List the multiples of 4 = 4, 8, 12, 16, …
Here, the common denominator of 1 /4 and 1 /2 is 8
So, the answer is 1/4 and 1/2
The correct answer is option b.
Question 3.
Which number is 100,000 more than seven hundred two thousand, eighty-three?
Options:
a. 703,083
b. 712,083
c. 730,083
d. 802,083
Answer: 802,083
Explanation:
100,000 + 702,083 = 802,083
The correct answer is option d.
Question 4.
Aiden baked 8 dozen muffins. How many total muffins did he bake?
Options:
a. 64
b. 80
c. 96
d. 104
Answer: 96
Explanation:
As per the given data,
Aiden baked 8 dozen muffins
1 dozen = 12
then, 8 dozens = 12 x 8 = 96
So, Aiden baked total 96 muffins.
The correct answer is option c.
Question 5.
On a bulletin board, the principal, Ms. Gomez, put 115 photos of the fourthgrade students in her school. She put the photos in 5 equal rows. How many photos did she put in each row?
Options:
a. 21
b. 23
c. 25
d. 32
Answer: 23
Explanation:
As per the given data,
On a bulletin board, the principal, Ms. Gomez, put 115 photos of the fourth-grade students in her school
She put the photos in 5 equal rows
Then, number of photos in each row = 115/5 = 23
So, Ms. Gomez put photos in each row = 23
The correct answer is option b.
Question 6.
Judy uses 12 tiles to make a mosaic. Eight of the tiles are blue. What fraction, in simplest form, represents the tiles that are blue?
Options:
a. \(\frac{2}{3}\)
b. \(\frac{2}{5}\)
c. \(\frac{3}{4}\)
d. \(\frac{12}{18}\)
Answer: \(\frac{2}{3}\)
Explanation:
As per the given data,
Judy uses 12 tiles to make a mosaic
Eight of the tiles are blue = 8/12
Divide the numerator and denominator of 8/12 with 4
(8 ÷ 4)/(12 ÷ 4) = 2/3
The simplest form of 8/12 is 2/3
The correct answer is option a.
Common Core – Fraction Equivalence and Comparison – Page No. 121
Question 1.
Miranda is braiding her hair. Then she will attach beads to the braid. She wants \(\frac{1}{3}\) of the beads to be red. If the greatest number of beads that will fit on the braid is 12, what other fractions could represent the part of the beads that are red?
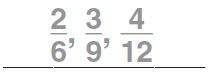
Explanation:
Miranda is braiding her hair. Then she will attach beads to the braid. She wants 1/3 of the beads to be red. If the greatest number of beads that will fit on the braid is 12.
1/3 × 2/2 = 2/6
1/3 × 3/3 = 3/9
1/3 × 4/4 = 4/12
Question 2.
Ms. Groves has trays of paints for students in her art class. Each tray has 5 colors. One of the colors is purple. What fraction of the colors in 20 trays is purple?
\(\frac{□}{□}\)
Answer: \(\frac{1}{5}\)
Explanation:
Given,
Ms. Groves has trays of paints for students in her art class.
Each tray has 5 colors.
If you have 20 trays that are 100 colors with 20 being purple. 20/ 100 is 1/5.
Question 3.
Miguel is making an obstacle course for field day. At the end of every sixth of the course, there is a tire. At the end of every third of the course, there is a cone. At the end of every half of the course, there is a hurdle. At which locations of the course will people need to go through more than one obstacle?
Type below:
_________
Answer: 1/3, 1/2, 2/3 and final locations
Explanation:
We have three fractions with different denominators: sixths, thirds, and halves.
The first step is to make all the denominators equal for 1/6, 1/3, 1/2.
In this case, we want sixths since LCM(2, 3, 6) = 6
since 1/3 = 2/6, and 1/2 = 3/6. Now we can start solving.
1. There are six tires at the following: 1/6, 2/6, 3/6, 4/6, 5/6, and 6/6.
2. There are three cones at the following (G.C.F.): 2/6 (or 1/3), 4/6 (or 2/3), and 6/6 (or 3/3).
3. There are two hurdles at the following (G.C.F.): 3/6 (or 1/2) and 6/6 (or 2/2).
We look for common numbers.
1. On 2/6, there are two obstacles: a tire and a cone.
2. On 3/6, there are two obstacles: a tire and a hurdle.
3. On 4/6, there are two obstacles: a tire and a cone.
4. At 6/6, there are three obstacles: a tire, cone, and a hurdle.
2/6 = 1/3
3/6 = 1/2
4/6 = 2/3
6/6 = 1
The answers are 1/3, 1/2, 2/3, and 1.
Question 4.
Preston works in a bakery where he puts muffins in boxes. He makes the following table to remind himself how many blueberry muffins should go in each box.

How many blueberry muffins should Preston put in a box with 36 muffins?
_________
Answer: 12 blueberry muffins
Explanation:
Preston works in a bakery where he puts muffins in boxes. He makes the following table to remind himself how many blueberry muffins should go in each box.
So, he had 2 blueberry muffins out of 6 muffins.
2/6 × 2/2 = 4/12. 4 blueberry muffins out of 12 muffins.
2/6 × 4/4 = 8/24. 8 blueberry muffins out of 24 muffins.
2/6 × 6/6 = 12/36. 12 blueberry muffins out of 36 muffins.
Common Core – Fraction Equivalence and Comparison – Page No. 122
Question 1.
A used bookstore will trade 2 of its books for 3 of yours. If Val brings in 18 books to trade, how many books can she get from the store?
Options:
a. 9
b. 12
c. 18
d. 27
Answer: 12
Explanation:
A used bookstore will trade 2 of its books for 3 of yours.
If Val brings in 18 books to trade 2/3 × 6/6 = 12/18, she gets 12 books.
Thus the correct answer is option b.
Question 2.
Every \(\frac{1}{2}\) hour Naomi stretches her neck; every \(\frac{1}{3}\) hour she stretches her legs; and every \(\frac{1}{6}\) hour she stretches her arms. Which parts of her body will Naomi stretch when \(\frac{2}{3}\) of an hour has passed?
Options:
a. neck and legs
b. neck and arms
c. legs and arms
d. none
Answer: legs and arms
Explanation:
Summing \(\frac{1}{2}\)‘s only gives integer values giving 1, 2, 3, 4…or
integer values +\(\frac{1}{2}\) and 0 + \(\frac{1}{2}\) = \(\frac{1}{2}\), 1 \(\frac{1}{2}\), 2 \(\frac{1}{2}\)…
So neck is excluded
Every \(\frac{1}{3}\): \(\frac{1}{3}\) + \(\frac{1}{2}\) = \(\frac{2}{3}\)
Legs will be stretched at \(\frac{2}{3}\) hour
Every \(\frac{1}{6}\): \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) = \(\frac{4}{6}\)
Divide top and bottom by 2 giving:
(4 ÷ 2)/(6 ÷ 2) = \(\frac{2}{3}\)
Arms will be stretched at \(\frac{2}{3}\) hour.
Thus the correct answer is option c.
Question 3.
At the beginning of the year, the Wong family car had been driven 14,539 miles. At the end of the year, their car had been driven 21,844 miles. How many miles did the Wong family drive their car during that year?
Options:
a. 6,315 miles
b. 7,295 miles
c. 7,305 miles
d. 36,383 miles
Answer: 7,305 miles
Explanation:
If at the beginning of the year, the Wong family’s car had driven 14539 miles and at the end of the year, it had driven 21844 miles, then subtract 14539 from 21844 to determine the difference between the two values, which will tell you how many miles the Wong family drove their car for during the year.
21844 – 14539 = 7305 miles
Thus the correct answer is option c.
Question 4.
Widget Company made 3,600 widgets in 4 hours. They made the same number of widgets each hour. How many widgets did the company make in one hour?
Options:
a. 80
b. 90
c. 800
d. 900
Answer: 900
Explanation:
3,600 widgets in 4 hours therefore 3,600 / 4 for one hour = 900 widgets 900 widgets in one hour.
Thus the correct answer is option d.
Question 5.
Tyler is thinking of a number that is divisible by 2 and by 3. By which of the following numbers must Tyler’s number also be divisible?
Options:
a. 6
b. 8
c. 9
d. 12
Answer: 6
Explanation:
The number 6 is divisible by 2 and by 3.
Thus the correct answer is option a.
Question 6.
Jessica drew a circle divided into 8 equal parts. She shaded 6 of the parts. Which fraction is equivalent to the part of the circle that is shaded?
Options:
a. \(\frac{2}{3}\)
b. \(\frac{3}{4}\)
c. \(\frac{10}{16}\)
d. \(\frac{12}{18}\)
Answer: \(\frac{3}{4}\)
Explanation:
Jessica drew a circle divided into 8 equal parts. She shaded 6 of the parts.
6/8 = 3/4
Thus the correct answer is option b.
Common Core – Fraction Equivalence and Comparison – Page No. 123
Compare. Write < or > .
Question 1.
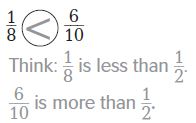
Answer:
18 < 610
Explanation:

Question 2.
\(\frac{4}{12}\) ______ \(\frac{4}{6}\)
Answer:
4/12 < 4/6
Explanation:
4/12 and 4/6
4/12 is less than 1/2
4/6 is greater than 1/2
So, 4/12 < 4/6
Question 3.
\(\frac{2}{8}\) ______ \(\frac{1}{2}\)
Answer:
2/8 < 1/2
Explanation:
2/8 and 1/2
2/8 is less than 1/2
1/2 is equal to 1/2
So, 2/8 < 1/2
Question 4.
\(\frac{3}{5}\) ______ \(\frac{3}{3}\)
Answer:
3/5 < 3/3
Explanation:
3/5 and 3/3
3/5 is greater than 1/2
3/3 is equal to 1
So, 3/5 < 3/3
Question 5.
\(\frac{7}{8}\) ______ \(\frac{5}{10}\)
Answer:
7/8 > 5/10
Explanation:
7/8 and 5/10
7/8 is greater than 1/2
5/10 is equal to 1/2
So, 5/10 < 7/8
Question 6.
\(\frac{9}{12}\) ______ \(\frac{1}{3}\)
Answer:
9/12 > 1/3
Explanation:
9/12 and 1/3
9/ 12 is greater than 1/2
1/3 is less than 1/2
1/3 < 9/12
Question 7.
\(\frac{4}{6}\) ______ \(\frac{7}{8}\)
Answer:
4/6 < 7/8
Explanation:
4/6 and 7/8
4/6 is greater than 1/2
7/8 is closer to 1
So, 4/6 < 7/8
Question 8.
\(\frac{2}{4}\) ______ \(\frac{2}{3}\)
Answer:
2/4 < 2/3
Explanation:
2/4 and 2/3
2/4 is equal to 1/2
2/3 is greater than 1/2
So, 2/4 < 2/3
Question 9.
\(\frac{3}{5}\) ______ \(\frac{1}{4}\)
Answer: 35 > 14
Explanation:
3/5 and 1/4
3/5 is greater than 1/2
1/4 is less than 1/2
So, 1/4 < 3/5
Question 10.
\(\frac{6}{10}\) ______ \(\frac{2}{5}\)
Answer:
6/10 > 2/5
Explanation:
6/10 and 2/5
6/10 is greater than 1/2
2/5 is less than 1/2
So, 2/5 < 6/10
Question 11.
\(\frac{1}{8}\) ______ \(\frac{2}{10}\)
Answer:
1/8 < 2/10
Explanation:
1/8 and 2/10
1/8 is less than 1/2
2/10 is less than 1/2 but greater than 1/8
So, 1/8 < 2/10
Question 12.
\(\frac{2}{3}\) ______ \(\frac{5}{12}\)
Answer:
2/3 > 5/12
Explanation:
2/3 and 5/12
2/3 is greater than 1/2
5/12 is less than 1/2
So, 5/12 < 2/3
Question 13.
\(\frac{4}{5}\) ______ \(\frac{5}{6}\)
Answer:
4/5< 5/6
Explanation:
4/5 and 5/6
4/5 is greater than 1/2
5/6 is greater than 1/2
Common denominator is 30
(4×6)/(5×6) and (5×5)/(6×5)
24/30 and 25/30
24/30 < 25/30
So, 4/5 < 5/6
Question 14.
\(\frac{3}{5}\) ______ \(\frac{5}{8}\)
Answer:
3/5 < 5/8
Explanation:
3/5 and 5/8
3/5 is greater than 1/2
5/8 is greater than 1/2
Common denominator is 40
(3×8)/(5×8) and (5×5)/(8×5)
24/40 and 25/ 40
24/40 < 25/40
3/5 < 5/8
Question 15.
\(\frac{8}{8}\) ______ \(\frac{3}{4}\)
Answer:
8/8 > 3/4
Explanation:
8/8 and 3/4
8/8 is equal to 1
3/4 is less than 1
3/4 < 8/8
Question 16.
Erika ran \(\frac{3}{8}\) mile. Maria ran \(\frac{3}{4}\) mile. Who ran farther?
__________
Answer: Maria
Explanation:
As per the data,
Erika ran 3/8 mile
Maria ran 3/4 mile
Multiply the numerator and denominator of 3/4 with 2
(3×2)/(4×2) = 6/8
3/8 < 6/8
So, 3/8 < 3/4
So, Maria ran faster than Erika
Question 17.
Carlos finished \(\frac{1}{3}\) of his art project on Monday. Tyler finished \(\frac{1}{2}\) of his art project on Monday. Who finished more of his art project on Monday?
__________
Answer:
Tyler
Explanation:
From the given data,
Carlos finished 1/3 of his art project on Monday
Tyler finished ½ of his art project on Monday
1/3 is less than 1/2
1/2 is equal to 1/2
So, 1/3 < 1/2
Then, Tyler finished more of his work on Monday
Common Core – Fraction Equivalence and Comparison – Page No. 124
Question 1.
Which symbol makes the statement true?
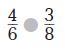
Options:
a. >
b. <
c. =
d. none
Answer:
a. >
Explanation:
4/6 ? 3/8
By comparing 4/6 with 1/2, 4/6 > 1/2
By comparing 3/8 with 1/2, 3/8 < 1/2
So, 4/6 > 3/8
Thus the correct answer is option a.
Question 2.
Which of the following fractions is greater than \(\frac{3}{4}\)?
Options:
a. \(\frac{1}{4}\)
b. \(\frac{5}{6}\)
c. \(\frac{3}{8}\)
d. \(\frac{2}{3}\)
Answer: b. 5/6
Explanation:
From the given data,
By comparing the 3/4 with 1/2, 3/4 > 1/2
Same as above, compare the options with ½
a. 1/4 < 1/2
b. 5/6 > 1/2
c. 3/8 < 1/2
d. 2/3 > 1/2
5/6 and 2/3 are greater than the 1/2
So, compare the 5/6 with 2/3
Then, 5/6 > 2/3
So, 5/6 > 3/4
Thus the correct answer is option b.
Question 3.
Abigail is putting tiles on a table top. She needs 48 tiles for each of 8 rows. Each row will have 6 white tiles. The rest of the tiles will be purple. How many purple tiles will she need?
Options:
a. 432
b. 384
c. 336
d. 48
Answer:
c. 336
Explanation:
As per the given data
Abigail is putting tiles on a table top
Number of rows = 8
She needs 48 tiles for each of row = 48×8 = 384
Number of white tiles per row = 6×8 = 48
The rest of the tiles will be purple = 384 – 48 =336
So, the total number of purple color tiles = 336
Thus the correct answer is option c.
Question 4.
Each school bus going on the field trip holds 36 students and 4 adults. There are 6 filled buses on the field trip. How many people are going on the field trip?
Options:
a. 216
b. 240
c. 256
d. 360
Answer:
b. 240
Explanation:
From the given data,
Each school bus going on the field trip holds 36 students and 4 adults
There are 6 filled buses on the field trip
6 x (36 + 4) = 6 x 40 = 240
So, the total number of people on the field trip = 240
Thus the correct answer is option b.
Question 5.
Noah wants to display his 72 collector’s flags. He is going to put 6 flags in each row. How many rows of flags will he have in his display?
Options:
a. 12
b. 15
c. 18
d. 21
Answer:
a. 12
Explanation:
As mentioned in the data,
Noah wants to display his 72 collector’s flag
He is going to put 6 flags in each row = 6x = 72
X = 12
So, a total 12 number of rows of flags will have in his display.
Thus the correct answer is option a.
Question 6.
Julian wrote this number pattern on the board:
3, 10, 17, 24, 31, 38.
Which of the numbers in Julian’s pattern are composite numbers?
Options:
a. 3, 17, 31
b. 10, 24, 38
c. 10, 17, 38
d. 17, 24, 38
Answer:
b. 10, 24, 38
Explanation:
As per the given information
Julian wrote his number pattern on the board =3, 10, 17, 24, 31, 38
Factors of 3 = 1,3
Factors of 10 = 1,2,5,10
Factors of 17 = 1, 17
Factors of 24 = 1, 2, 3, 4, 6
Factors of 31 = 1, 31
Factors of 38 = 1, 2, 19, 38
So, the composite number is 10, 24, and 38, which numbers have more than 2 factors.
Thus the correct answer is option b.
Common Core – Fraction Equivalence and Comparison – Page No. 125
Compare. Write <, >, or =
Question 1.
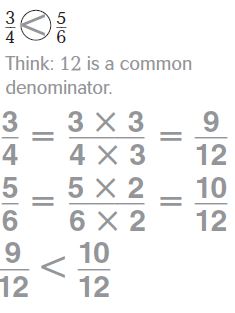
Answer:
1/5 < 2/10
Explanation:

Question 2.
\(\frac{1}{5}\) ______ \(\frac{2}{10}\)
Answer:
1/5 = 2/10
Explanation:
1/5 and 2/10
Think: 10 is a common denominator
1/5 = (1×2) / (5×2) = 2/10
2/10 = 2/10
So, 1/5 = 2/10
Question 3.
\(\frac{2}{4}\) ______ \(\frac{2}{5}\)
Answer:
2/4 > 2/5
Explanation:
2/4 and 2/5
20 is a common denominator
2/4 = (2×5)/(4×5) = 10/20
2/5 = (2×4)/(5×4) = 8/20
10/20 > 8/20
So, 2/4 > 2/5
Question 4.
\(\frac{3}{5}\) ______ \(\frac{7}{10}\)
Answer:
3/5 < 7/10
Explanation:
3/5 and 7/10
10 is a common denominator
3/5 = (3×2)/(5×2) = 6/10
7/10
6/10 < 7/10
So, 3/5 < 7/10
Question 5.
\(\frac{4}{12}\) ______ \(\frac{1}{6}\)
Answer:
4/12 > 1/6
Explanation:
4/12 and 1/6
12 is a common denominator
4/12
1/6 = (1×2)/(6×2) = 2/12
4/12 > 2/12
So, 4/12 > 1/6
Question 6.
\(\frac{2}{6}\) ______ \(\frac{1}{3}\)
Answer:
2/6 = 1/3
Explanation:
2/6 and 1/3
6 is a common denominator
2/6
1/3 = (1×2)/(3×2) = 2/6
So, 2/6 =2/6
So, 2/6 = 1/3
Question 7.
\(\frac{1}{3}\) ______ \(\frac{2}{4}\)
Answer:
1/3 < 2/4
Explanation:
1/3 and 2/4
12 is a common denominator
1/3 = (1×4)/(3×4) = 4/12
2/4 = (2×3)/(4×3) = 6/12
4/12 < 6/12
So, 1/3 < 2/4
Question 8.
\(\frac{2}{5}\) ______ \(\frac{1}{2}\).
Answer:
2/5 < 1/2
Explanation:
2/5 and 1/2
10 is a common denominator
2/5 = (2×2)/(5×2) = 4/10
1/2 = (1×5)/(2×5) = 5/10
4/10 < 5/10
So, 2/5 < 1/2
Question 9.
\(\frac{4}{8}\) ______ \(\frac{2}{4}\)
Answer:
4/8 = 2/4
Explanation:
4/8 and 2/4
8 is a common denominator
4/8
2/4 = (2×2)/(4×2) = 4/8
2/4 = 4/8
So, 4/8 = 2/4
Question 10.
\(\frac{7}{12}\) ______ \(\frac{2}{4}\)
Answer:
7/12 < 2/4
Explanation:
7/12 and 2/4
12 is a common denominator
7/12
2/4 = (2×3)/(4×3) = 6/12
7/12 < 6/12
So, 7/12 < 2/4
Question 11.
\(\frac{1}{8}\) ______ \(\frac{3}{4}\)
Answer:
1/8 < 3/4
Explanation:
1/8 and 3/4
8 is a common denominator
1/8
3/4 = (3×2)/(4×2) = 6/8
1/8 < 6/8
So, 1/8 < 3/4
Question 12.
A recipe uses \(\frac{2}{3}\) of flour and \(\frac{5}{8}\) cup of blueberries. Is there more flour or more blueberries in the recipe?
more _________
Answer: flour
Explanation:
From the given data,
A recipe uses 2/3 of flour and 5/8 cup of blueberries
The common denominator is 24
2/3 = (2×8)/(3×8) = 16/24
5/8 = (5×3)/(8×3) = 15/24
16/24 > 15/24
So, 2/3 > 5/8
So, flour is more in the recipe
Question 13.
Peggy completed \(\frac{5}{6}\) of the math homework and Al completed \(\frac{4}{5}\) of the math homework. Did Peggy or Al complete more of the math homework?
_________
Answer:
Peggy completed more work than Al
Explanation:
As per the given data,
Peggy completed 5/6 of the math homework
A1 completed 4/5 of the math homework
30 is a common denominator
5/6 = (5×5)/(6×5) = 25/30
4/5 = (4×6)/(5×6) =24/30
25/30 > 24/30
So, 5/6 > 4/5
So, Peggy completed more work than Al
Common Core – Fraction Equivalence and Comparison – Page No. 126
Question 1.
Pedro fills a glass \(\frac{2}{4}\) full with orange juice. Which of the following fractions is greater than \(\frac{2}{4}\)?
Options:
a. \(\frac{3}{8}\)
b. \(\frac{4}{6}\)
c. \(\frac{5}{12}\)
d. \(\frac{1}{3}\)
Answer:
b. 46
Explanation:
46 > 24
Thus the correct answer is option b.
Question 2.
Today Ian wants to run less than \(\frac{7}{12}\) mile. Which of the following distances is less than \(\frac{7}{12}\) mile?
Options:
a. \(\frac{3}{4}\) mile
b. \(\frac{2}{3}\) mile
c. \(\frac{5}{6}\) mile
d. \(\frac{2}{4}\) mile
Answer:
d. 2/4 mile
Explanation:
2/4 is less than 7/12
Thus the correct answer is option d.
Question 3.
Ms. Davis traveled 372,645 miles last year on business. What is the value of 6 in 372,645?
Options:
a. 6
b. 60
c. 600
d. 6,000
Answer:
c. 600
Explanation:
Ms. Davis traveled 372, 645 miles last year on business
The value of 6 in 372,645 is 600.
Thus the correct answer is option c.
Question 4.
One section of an auditorium has 12 rows of seats. Each row has 13 seats. What is the total number of seats in that section?
Options:
a. 25
b. 144
c. 156
d. 169
Answer:
c. 156
Explanation:
From the given information
One section of an auditorium has 12 rows of seats
Each row has 13 seats = 13×12 = 156 seats
So, the total number of seats in the auditorium = 156 seats
Thus the correct answer is option c.
Question 5.
Sam has 12 black-and-white photos and 18 color photos. He wants to put the photos in equal rows so each row has either black-and-white photos only or color photos only. In how many rows can Sam arrange the photos?
Options:
a. 1, 2, 3, or 6 rows
b. 1, 3, 6, or 9 rows
c. 1, 2, or 4 rows
d. 1, 2, 3, 4, 6, or 9 rows
Answer:
a. 1, 2, 3, or 6 rows
Explanation:
As per the given information
Sam has 12 black and white photos 18 color photos
He wants to put the photos in equal rows
So each row has either black and white photos only or color photos only
H.C.F of 12 and 18 is 6
Rows of 6.
2 rows of black equal 12.
3 rows of white equals 18.
Thus the correct answer is option a.
Question 6.
The teacher writes \(\frac{10}{12}\) on the board. He asks students to write the fraction in the simplest form. Who writes the correct answer?
Options:
a. JoAnn writes \(\frac{10}{12}\)
b. Karen writes \(\frac{5}{12}\)
c. Lynn writes \(\frac{6}{5}\)
d. Mark writes \(\frac{5}{6}\)
Answer:
d. Mark writes 56
Explanation:
As per the given data,
The teacher writes 10/12 on the board
He asks students to write the fraction in simplest form
For the simplest form of 10/12, divide the 10/12 with 2
(10÷2)/(12÷2) = 5/6
5/6 is the simplest form of 10/12
So, Mark writes the correct answer.
Thus the correct answer is option d.
Common Core – Fraction Equivalence and Comparison – Page No. 127
Write the fractions in order from least to greatest.
Question 1.
\(\frac{5}{8}, \frac{2}{12}, \frac{8}{10}\)
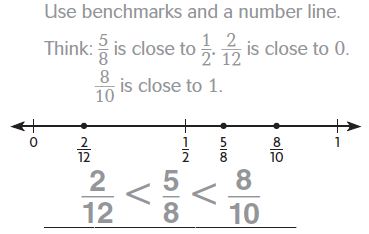
Answer:
2/12, 5/8, 8/10
Explanation:

Question 2.
\(\frac{1}{5}, \frac{2}{3}, \frac{5}{8}\)
Type below:
_________
Answer:
1/5, 5/8, 2/3
Explanation:

1/5, 2/3, 5/8
1/5 is closer to 0
2/3 is greater than 1/2
5/8 greater than 1/2
1/5 < 5/8 < 2/3
Question 3.
\(\frac{1}{2}, \frac{2}{5}, \frac{6}{10}\)
Type below:
_________
Answer:
2/5, 1/2, 6/10
Explanation:

1/2, 2/5, 6/10
1/2 is equal to 1/2
2/5 is less than 1/2
6/10 is greater than 1/2
Question 4.
\(\frac{4}{6}, \frac{7}{12}, \frac{5}{10}\)
Type below:
_________
Answer:
5/10 < 7/12 < 4/6
Explanation:

4/6, 7/12, 5/10
4/6 is closer to 1
7/12 is greater than 1/2
5/10 is equal to 1/2
Question 5.
\(\frac{1}{4}, \frac{3}{6}, \frac{1}{8}\)
Type below:
_________
Answer:
18 < 14 < 36
Explanation:

1/4, 3/6, 1/8
1/4 is less than 1/2
3/6 is equal to 1/2
1/8 is closer to 0
Question 6.
\(\frac{1}{8}, \frac{3}{6}, \frac{7}{12}\)
Type below:
_________
Answer:
1/8 < 7/12 < 3/6
Explanation:

1/8, 3/6, 7/12
1/8 is closer to 0
3/6 is equal to 1/2
7/12 is greater than 1/2
Question 7.
\(\frac{8}{100}, \frac{3}{5}, \frac{7}{10}\)
Type below:
_________
Answer:
8/100 < 3/5 < 7/10
Explanation:

8/100, 3/5, 7/10
8/100 is closer to 0
3/5 is greater than 1/2
7/10 is closer to 1
Question 8.
\(\frac{3}{4}, \frac{7}{8}, \frac{1}{5}\)
Type below:
_________
Answer:
15 < 34 < 78
Explanation:

3/4, 7/8, 1/5
3/4 is greater than 1/2
7/8 is closer to 1
1/5 is closer to 0
Question 9.
Amy’s math notebook weighs \(\frac{1}{2}\) pound, her science notebook weighs \(\frac{7}{8}\) pound, and her history notebook weighs \(\frac{3}{4}\) pound. What are the weights in order from lightest to heaviest?
Type below:
__________
Answer:
12 pound, 34 pound, 78 pound
Explanation:
From the given data,
Amy’s math notebook weighs 1/2 pound
Science notebook weighs 7/8 pound
History notebook weighs 3/4 pound
7/8 is closer to 1
3/4 is greater than 1/2
1/2 < 3/4 < 7/8
So, Amy’s math notebook weight < history notebook weight < science notebook
Question 10.
Carl has three picture frames. The thicknesses of the frames are \(\frac{4}{5}\) inch, \(\frac{3}{12}\) inch, and \(\frac{5}{6}\) inch. What are the thicknesses in order from least to greatest?
Type below:
__________
Answer:
3/12 inch, 4/5 inch, 5/6 inch
Explanation:
As per the given data,
Carl has three picture frames
The thickness of the frames are 4/5 inch, 3/12 inch, 5/6 inch
4/5 is greater than 1/2
3/12 is less than 1/2
5/6 is closer to 1
3/12 < 4/5 < 5/6
Common Core – Fraction Equivalence and Comparison – Page No. 128
Question 1.
Juan’s three math quizzes this week took him \(\frac{1}{3}\) hour, \(\frac{4}{6}\) hour, and \(\frac{1}{5}\) hour to complete. Which list shows the lengths of time in order from least to greatest?
Options:
a. \(\frac{1}{3} hour, \frac{4}{6} hour, \frac{1}{5} hour\)
b. \(\frac{1}{5} hour, \frac{1}{3} hour, \frac{4}{6} hour\)
c. \(\frac{1}{3} hour, \frac{1}{5} hour, \frac{4}{6} hour\)
d. \(\frac{4}{6} hour, \frac{1}{3} hour, \frac{1}{5} hour\)
Answer:
b. 1/5 hour, 1/3 hour, 4/6 hour
Explanation:
From the given information
Juan’s three math quizzes this week took him 1/3 hour, 4/6 hour, and 1/5 hour
Compare 1/3 and 1/2
1/3 is less than 1/2
4/6 is greater than 1/2
1/5 is closer to 0
1/5 < 1/3 < 4/6
So, Juan’s math quizzes times from least to greatest is 1/5, 1/3, 4/6
Thus the correct answer is option b.
Question 2.
On three days last week, Maria ran \(\frac{3}{4}\) mile, \(\frac{7}{8}\) mile, and \(\frac{3}{5}\) mile. What are the distances in order from least to greatest?
Options:
a. \(\frac{3}{4} mile, \frac{7}{8} mile, \frac{3}{5} mile\)
b. \(\frac{3}{5} mile, \frac{3}{4} mile, \frac{7}{8} mile\)
c. \(\frac{7}{8} mile, \frac{3}{4} mile, \frac{3}{5} mile\)
d. \(\frac{7}{8} mile, \frac{3}{5} mile, \frac{3}{4} mile\)
Answer:
b. 3/5 mile, 3/4 mile, 7/8 mile
Explanation:
As per the information
On three days last week, Maria ran 3/4 mile, 7/8 mile, and 3/5 mile
3/4 is greater than 1/2
7/8 is closer to 1
3/5 is greater than 1/2
Compare 3/5 and 3/4
3/4 is greater than 3/5
So, 3/5 < 3/4 < 7/8
Distance from least to greatest is 3/5, 3/4 , 7/8
Thus the correct answer is option b.
Question 3.
Santiago collects 435 cents in nickels. How many nickels does he collect?
Options:
a. 58
b. 78
c. 85
d. 87
Answer:
d. 87
Explanation:
As per the given data,
Santiago collects 435 cents in nickels
1 nickel worth is 5 cents
Then, nickels per 435 cents = 435/5 = 87
So, Santiago collects 87 nickels.
Thus the correct answer is option d.
Question 4.
Lisa has three classes that each last 50 minutes. What is the total number of minutes the three classes last?
Options:
a. 15 minutes
b. 150 minutes
c. 153 minutes
d. 156 minutes
Answer:
b. 150 minutes
Explanation:
From the given data,
Lisa has three classes that each last 50 minutes
The total number of minutes the three classes last = 3×50 =150 minutes.
Thus the correct answer is option b.
Question 5.
Some students were asked to write a composite number. Which student did NOT write a composite number?
Options:
a. Alicia wrote 2.
b. Bob wrote 9.
c. Arianna wrote 15.
d. Daniel wrote 21.
Answer:
a. Alicia wrote 2.
Explanation:
As per the information
Some students were asked to write a composite number
a. Alicia wrote 2
Factors of 2 is 1 and 2
b. Bob wrote 9
Factors of 9 is 1, 3, 9
c. Arianna wrote 15
Factors of 15 is 1, 3, 5, 15
d. Daniel wrote 21
Factors of 21 is 1,3,7,21
So, Alicia did not write a composite number.
Thus the correct answer is option a.
Question 6.
Mrs. Carmel serves \(\frac{6}{8}\) of a loaf of bread with dinner. Which fraction is equivalent to \(\frac{6}{8}\) ?
Options:
a. \(\frac{2}{4}\)
b. \(\frac{9}{16}\)
c. \(\frac{2}{3}\)
d. \(\frac{3}{4}\)
Answer: d. 3/4
Explanation:
As per the given information
Mrs. Carmel serves 6/8 of a loaf of bread with dinner
To find the equivalent fraction of 6/8, simplify the 6/8 by dividing with the 2
(6÷2)/(8÷2) = 3/4
So, the equivalent fraction of 6/8 is 3/4
Thus the correct answer is option d.
Common Core – Fraction Equivalence and Comparison – Page No. 129
Lesson 6.1
Tell whether the fractions are equivalent. Write = or ≠.
Question 1.
\(\frac{5}{10}\) ______ \(\frac{1}{2}\)
Answer: \(\frac{5}{10}\) = \(\frac{1}{2}\)
Explanation:
Divide \(\frac{5}{10}\) by 2
\(\frac{5}{10}\) ÷ 5 = \(\frac{1}{2}\)
So, \(\frac{5}{10}\) = \(\frac{1}{2}\)
Question 2.
\(\frac{2}{3}\) ______ \(\frac{3}{6}\)
Answer: \(\frac{2}{3}\) ≠ \(\frac{3}{6}\)
Explanation:
The fraction \(\frac{2}{3}\) is not equal to \(\frac{3}{6}\)
Question 3.
\(\frac{6}{8}\) ______ \(\frac{3}{4}\)
Answer: \(\frac{6}{8}\) = \(\frac{3}{4}\)
Explanation:
Divide \(\frac{6}{8}\) by 2.
\(\frac{6}{8}\) ÷ 2 = \(\frac{3}{4}\)
So, \(\frac{6}{8}\) = \(\frac{3}{4}\)
Question 4.
\(\frac{7}{12}\) ______ \(\frac{4}{6}\)
Answer: \(\frac{7}{12}\) ≠ \(\frac{4}{6}\)
Explanation:
The fraction \(\frac{7}{12}\) is not equal to \(\frac{4}{6}\).
Lesson 6.2
Write two equivalent fractions for each.
Question 5.
\(\frac{2}{3}\)
Type below:
_________
Answer: 4/6 and 8/12
Explanation:
2/3
(2/3) x (2/2) = 4/6
(2/3) x (4/4) = 8/12
Then, the equivalent fractions of 2/3 = 4/6 and 8/12
Question 6.
\(\frac{5}{10}\)
Type below:
_________
Answer: 1/2
Explanation:
\(\frac{5}{10}\) × 2/2 = 10/20
\(\frac{5}{10}\) ÷ 5 = 1/2
Question 7.
\(\frac{4}{12}\)
Type below:
_________
Answer: 1/3
Explanation:
\(\frac{4}{12}\) ÷ 3 = 1/3
\(\frac{4}{12}\) × 3/3 = 4/12
Question 8.
\(\frac{4}{5}\)
Type below:
_________
Answer:
8/10 and 80/100
Explanation:
4/5
(4/5) x (2/2) = 8/10
(4/5) x (20/20) = 80/100
Then, the equivalent fractions of 4/5 = 8/10 and 80/100
Lesson 6.3
Write the fraction in simplest form.
Question 9.
\(\frac{6}{12}\)
\(\frac{□}{□}\)
Answer:
1/2
Explanation:
6/12 in simplest form
Divide the 6/12 with 6
(6/6)/(12/6) = 1/2
So, the simplest form of 6/12 is 1/2
Question 10.
\(\frac{2}{10}\)
\(\frac{□}{□}\)
Answer:
1/5
Explanation:
2/10 in simplest form
Divide the 2/10 with 2
(2/2)/(10/2) = 1/5
So, the simplest form of 2/10 is 1/5
Question 11.
\(\frac{4}{6}\)
\(\frac{□}{□}\)
Answer:
2/3
Explanation:
4/6 in simplest form
Divide the 4/6 with 2
(4/2)/(6/2) = 2/3
So, the simplest form of 4/6 is 2/3
Question 12.
\(\frac{3}{12}\)
\(\frac{□}{□}\)
Answer: 1/4
Explanation:
3/12 in the simplest form
Divide 3/12 with 3.
3/12 ÷ 3 = 1/4
So the simplest form of \(\frac{3}{12}\) is \(\frac{1}{4}\)
Question 13.
\(\frac{6}{10}\)
\(\frac{□}{□}\)
Answer: 3/5
Explanation:
\(\frac{6}{10}\) in the simplest form.
Divide the \(\frac{6}{10}\) with 2
\(\frac{6}{10}\) ÷ 2 = \(\frac{3}{5}\)
Lesson 6.4
Write the pair of fractions as a pair of fractions with a common denominator.
Question 14.
\(\frac{2}{3} \text { and } \frac{5}{6}\)
Type below:
_________
Answer: 8/12 and 10/12
Explanation:
The common denominator of \(\frac{2}{3} \text { and } \frac{5}{6}\)
List the multiples of 3 = 3, 6, 9, 12, 15, 18, 21,….
List the multiples of 6 = 6, 12, 18, 24, 30, 36, ….
Then, the common denominator of \(\frac{2}{3} \text { and } \frac{5}{6}\) is 12
For the Common pair of fractions, multiply the common denominator with fractions
So, common pair of fractions = 8/12 and 10/12
Question 15.
\(\frac{3}{5} \text { and } \frac{1}{2}\)
Type below:
_________
Answer: 6/10 and 5/10
Explanation:
Common denominator of \(\frac{3}{5} \text { and } \frac{1}{2}\)
List the multiples of 5 = 5, 10, 15, 20, 25, 30, …..
List the multiples of 2 = 2, 4, 6, 8, 10, 12, 14, 16, 18, 20….
Then, the common denominator of \(\frac{3}{5} \text { and } \frac{1}{2}\) is 10.
For the Common pair of fractions, multiply the common denominator with fractions
So, the common pair of fractions = 6/10 and 5/10.
Question 16.
\(\frac{1}{4} \text { and } \frac{5}{12}\)
Type below:
_________
Answer: 3/12 and 5/12
Explanation:
The common denominator of \(\frac{1}{4} \text { and } \frac{5}{12}\)
List the multiples of 4 = 4, 8, 12, 16, 20, 24, . . .
List the multiples of 12 = 12, 24, 36, 48…
Then, the common denominator of \(\frac{1}{4} \text { and } \frac{5}{12}\) is 12
For the Common pair of fractions, multiply the common denominator with fractions
So, common pair of fractions = 3/12 and 5/12.
Question 17.
\(\frac{7}{8} \text { and } \frac{3}{4}\)
Type below:
_________
Answer: 7/8 and 6/8
Explanation:
Common denominator of \(\frac{7}{8} \text { and } \frac{3}{4}\)
List the multiples of 8 = 8, 16, 24, 32, . . . .
List the multiples of 4 = 4, 8, 12, 16,….
Then, the common denominator of \(\frac{7}{8} \text { and } \frac{3}{4}\) is 8
For the Common pair of fractions, multiply the common denominator with fractions
So, the common pair of fractions = 7/8 and 6/8
Question 18.
\(\frac{3}{10} \text { and } \frac{1}{5}\)
Type below:
_________
Answer: \(\frac{3}{10} \text { and } \frac{2}{10}\)
Explanation:
Common denominator of \(\frac{3}{10} \text { and } \frac{1}{5}\)
List the multiples of 5 = 5, 10, 15, 20, 25, 30, …..
List the multiples of 10 = 10, 20, 30, 40, 50 ….
Then, the common denominator of \(\frac{3}{10} \text { and } \frac{1}{5}\) is 10
For the Common pair of fractions, multiply the common denominator with fractions
So, the common pair of fractions = \(\frac{3}{10} \text { and } \frac{2}{10}\)
Question 19.
\(\frac{3}{4} \text { and } \frac{1}{3}\)
Type below:
_________
Answer: 9/12 and 4/12
Explanation:
The common denominator of \(\frac{3}{4} \text { and } \frac{1}{3}\)
List the multiples of 3 = 3, 6, 9, 12, 15, 18, 21, 24, ….
List the multiples of 4 = 4, 8, 12, 16, 20, 24, . . .
Then, the common denominator of \(\frac{3}{4} \text { and } \frac{1}{3}\) is 12
For the Common pair of fractions, multiply the common denominator with fractions
So, the common pair of fractions = 9/12 and 4/12
Common Core – Fraction Equivalence and Comparison – Page No. 130
Lesson 6.5
Question 1.
Mr. Renner is decorating a bulletin board with groups of shapes. Each group has 3 shapes, and \(\frac{2}{3}\) of the shapes are snowflakes. If Mr. Renner is using 4 groups of shapes, how many snowflakes will he need? Complete the table to find the fraction of the shapes for each number of group that are
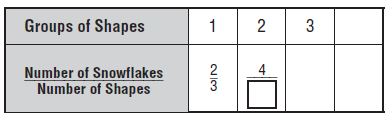
How many snowflake shapes will Mr. Renner use?
_______ snowflakes shapes
Answer: 8 snowflakes shapes
Explanation:
Given,
Mr. Renner is decorating a bulletin board with groups of shapes.
Each group has 3 shapes, and \(\frac{2}{3}\) of the shapes are snowflakes.
There are 4 groups and in every group, there are 2 snowflakes so in total there are 8. because 4 × 2=8
Mr. Renner uses 8 snowflakes shapes.
Question 2.
Nell made a pizza. She cut the pizza into fourths. Then she cut each fourth into four pieces. Nell and her friends ate 6 of the smaller pieces of the pizza.
What fraction of the pizza did Nell and her friends eat?
What fraction of the pizza did Nell and her friends NOT eat?
Answer:
okay so four is slice, and then do it again. the answer is at the bottom,
pizza: 16 pieces
Nell and her friends ate 6 smaller pizza
3/8 is the answer.
Lesson 6.6 – 6.7
Compare. Write <,>, or =.
Question 3.
\(\frac{2}{6}\) ______ \(\frac{3}{4}\)
Answer: \(\frac{2}{6}\) < \(\frac{3}{4}\)
Explanation:
\(\frac{2}{6}\) = \(\frac{1}{3}\)
\(\frac{1}{3}\) is less than \(\frac{3}{4}\)
So, \(\frac{2}{6}\) < \(\frac{3}{4}\)
Question 4.
\(\frac{6}{8}\) ______ \(\frac{1}{4}\)
Answer: \(\frac{6}{8}\) > \(\frac{1}{4}\)
Explanation:
\(\frac{6}{8}\) = \(\frac{3}{4}\)
\(\frac{3}{4}\) is greater than \(\frac{1}{4}\)
So, \(\frac{6}{8}\) > \(\frac{1}{4}\)
Question 5.
\(\frac{5}{6}\) ______ \(\frac{2}{4}\)
Answer: \(\frac{5}{6}\) > \(\frac{2}{4}\)
Explanation:
\(\frac{2}{4}\) = \(\frac{1}{2}\)
\(\frac{5}{6}\) is greater than \(\frac{1}{2}\)
So, \(\frac{5}{6}\) > \(\frac{2}{4}\)
Question 6.
\(\frac{1}{3}\) ______ \(\frac{4}{12}\)
Answer: \(\frac{1}{3}\) = \(\frac{4}{12}\)
Explanation:
\(\frac{4}{12}\) = \(\frac{1}{3}\)
\(\frac{1}{3}\) = \(\frac{4}{12}\)
Question 7.
\(\frac{1}{6}\) ______ \(\frac{1}{8}\)
Answer: \(\frac{1}{6}\) > \(\frac{1}{8}\)
Explanation:
Given the fractions \(\frac{1}{6}\) and \(\frac{1}{8}\)
Here the numerators are same so we have to compare the denominators.
The denominator with the smallest number will be the greatest fraction.
\(\frac{1}{6}\) is greater than \(\frac{1}{8}\)
So, \(\frac{1}{6}\) > \(\frac{1}{8}\)
Question 8.
\(\frac{2}{3}\) ______ \(\frac{4}{6}\)
Answer: \(\frac{2}{3}\) = \(\frac{4}{6}\)
Explanation:
\(\frac{4}{6}\) ÷ 2 = \(\frac{2}{3}\)
\(\frac{2}{3}\) = \(\frac{2}{3}\)
So, \(\frac{2}{3}\) = \(\frac{4}{6}\)
Question 9.
\(\frac{3}{10}\) ______ \(\frac{3}{12}\)
Answer: \(\frac{3}{10}\) > \(\frac{3}{12}\)
Explanation:
Given the fractions \(\frac{3}{10}\) and \(\frac{3}{12}\)
Here the numerators are same so we have to compare the denominators.
The denominator with the smallest number will be the greatest fraction.
Thus \(\frac{3}{10}\) > \(\frac{3}{12}\)
Question 10.
\(\frac{7}{8}\) ______ \(\frac{4}{4}\)
Answer: \(\frac{7}{8}\) < \(\frac{4}{4}\)
Explanation:
\(\frac{4}{4}\) = 1
1 is greater than \(\frac{7}{8}\)
Thus \(\frac{7}{8}\) < \(\frac{4}{4}\)
Lesson 6.8
Write the fractions in order from least to greatest.
Question 12.
\(\frac{1}{2}, \frac{1}{4}, \frac{5}{8}\)
Type below:
__________
Answer: 1/4, 5/8 and 1/2
Explanation:
1/4 × 2/2 = 2/8
5/8 × 1/1 = 5/8
1/2 × 4/4 = 4/8
Compare the numerators of the above fractions.
The numerator with the largest number will be the greatest fraction.
The fraction from least to greatest is 1/4, 5/8 and 1/2
Question 13.
\(\frac{2}{3}, \frac{1}{6}, \frac{9}{10}\)
Type below:
__________
Answer: 1/6, 2/3 and 9/10
Explanation:
Given the fractions \(\frac{2}{3}, \frac{1}{6}, \frac{9}{10}\)
2/3 × 10/10 = 20/30
1/6 × 5/5 = 5/30
9/10 × 3/3 = 27/30
Compare the numerators of the above fractions.
The numerator with the largest number will be the greatest fraction.
The fraction from least to greatest is 1/6, 2/3 and 9/10.
Question 14.
\(\frac{3}{5}, \frac{3}{4}, \frac{3}{8}\)
Type below:
__________
Answer: \(\frac{3}{8}, \frac{3}{5}, \frac{3}{4}\)
Explanation:
Given the fractions \(\frac{3}{5}, \frac{3}{4}, \frac{3}{8}\)
Here the numerators are the same so we have to compare the denominators.
The denominator with the smallest number will be the greatest fraction.
Thus the fractions from least to greatest are \(\frac{3}{8}, \frac{3}{5}, \frac{3}{4}\).
Conclusion:
I think the explained answers provided in this chapter are important for all 4th-grade students. Make sure to share these pdf links with our friends and assist them while practicing mathematical concepts. In case, do you feel anything is missing in Homework Practice FL, you can refer to the Go Math Grade 4 Answer Key Chapter 6 Fraction Equivalence and Comparison. Try solving these chapter problems and enhance your subject knowledge.
