Go Math Grade 4 Answer Key Chapter 9 Relate Fractions and Decimals assists you to examine your preparation level. Get numerous practice questions and exercise questions of Chapter 9 from the 4th Grade Go Math Answer Key Ch 9 Relate Fractions and Decimals and secure high marks. We have provided step-by-step solutions for all the problems covered in HMH Go math Grade 4 Answer Key Chapter Test, Practice Test, Assessment Tests. So that you can understand the Chapter 9 topics very easily.
HMH Go Math Grade 4 Chapter 9 Relate Fractions and Decimals Answer Key
While practicing the concepts of Chapter 9 Relate Fractions and Decimals, click on the links available over here and download the HMH Go Math Grade 4 Chapter 9 Relate Fractions and Decimals Solution Key for free. Hence, students can seek help to examine their strengths and weaknesses using the 4th Grade HMH Go Math Ch 9 Relate Fractions and Decimals Answer Key.
Lesson 1: Relate Tenths and Decimals
Lesson 2: Relate Hundredths and Decimals
- Relate Hundredths and Decimals – Page No. 503
- Relate Hundredths and Decimals Lesson Check – Page No. 504
- Relate Hundredths and Decimals Lesson Check 1 – Page No. 505
- Relate Hundredths and Decimals Lesson Check 2 – Page No. 506
Lesson 3: Equivalent Fractions and Decimals
- Equivalent Fractions and Decimals – Page No. 509
- Equivalent Fractions and Decimals Lesson Check – Page No. 510
- Equivalent Fractions and Decimals Lesson Check 1 – Page No. 511
- Equivalent Fractions and Decimals Lesson Check 2 – Page No. 512
Lesson 4: Relate Fractions, Decimals, and Money
- Relate Fractions, Decimals, and Money – Page No. 515
- Relate Fractions, Decimals, and Money Lesson Check – Page No. 516
- Relate Fractions, Decimals, and Money Lesson Check 1 – Page No. 517
- Relate Fractions, Decimals, and Money Lesson Check 2 – Page No. 518
Lesson 5: Problem Solving • Money
- Money – Page No. 521
- Money Lesson Check – Page No. 522
- Money Lesson Check 1 – Page No. 523
- Money Lesson Check 2 – Page No. 524
Mid-Chapter Checkpoint
Lesson 6: Add Fraction Parts of 10 and 100
- Add Fraction Parts of 10 and 100 – Page No. 529
- Add Fraction Parts of 10 and 100 Lesson Check – Page No. 530
- Add Fraction Parts of 10 and 100 Lesson Check 1 – Page No. 531
- Add Fraction Parts of 10 and 100 Lesson Check 2 – Page No. 532
Lesson 7: Compare Decimals
- Compare Decimals – Page No. 535
- Compare Decimals Lesson Check – Page No. 536
- Compare Decimals Lesson Check 1 – Page No. 537
- Compare Decimals Lesson Check 2 – Page No. 538
Review/Test
- Review/Test – Page No. 539
- Review/Test – Page No. 540
- Review/Test – Page No. 541
- Review/Test – Page No. 542
- Review/Test – Page No. 543
- Review/Test – Page No. 544
- Review/Test – Page No. 551
- Review/Test – Page No. 552
Common Core – New – Page No. 499
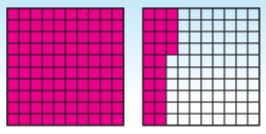
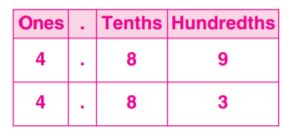
Relate Tenths and Decimals
Write the fraction or mixed number and the decimal shown by the model.
Question 1
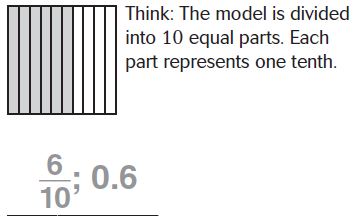
Answer:

Question 2.
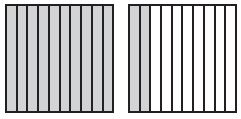
Type below:
________
Answer:
1\(\frac{2}{10}\)
Explanation:
The model is divided into 10 equal parts. Each part represents one-tenth.
1 2/10 is 1 whole and 2 tenths.
Question 3.
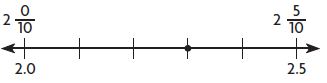
Type below:
________
Answer:
2\(\frac{3}{10}\) = 2.3
Explanation:
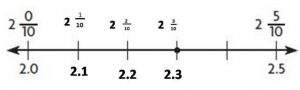
Question 4.
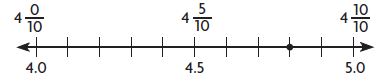
Type below:
________
Answer:
4\(\frac{8}{10}\) = 4.8
Explanation:
Write the fraction or mixed number as a decimal.
Question 5.
\(\frac{4}{10}\)
_____
Answer:
0.4
Explanation:
Write down 4 with the decimal point 1 space from the right (because 10 has 1 zero)
0.4
Question 6.
3 \(\frac{1}{10}\)
_____
Answer:
3.1
Explanation:
Multiply 3 x 10 = 30.
Add 30 + 1 = 31.
So, 31/10.
Write down 31 with the decimal point 1 space from the right (because 10 has 1 zero)
3.1
Question 7.
\(\frac{7}{10}\)
_____
Answer:
0.7
Explanation:
Write down 7 with the decimal point 1 space from the right (because 10 has 1 zero)
0.7
Question 8.
6 \(\frac{5}{10}\)
_____
Answer:
6.5
Explanation:
Multiply 6 x 10 = 60.
Add 60 + 5 = 65.
So, 65/10.
Write down 35 with the decimal point 1 space from the right (because 10 has 1 zero)
6.5
Question 9.
\(\frac{9}{10}\)
_____
Answer:
0.9
Explanation:
Write down 9 with the decimal point 1 space from the right (because 10 has 1 zero)
0.9
Problem Solving
Question 10.
There are 10 sports balls in the equipment closet. Three are kickballs. Write the portion of the balls that are kickballs as a fraction, as a decimal, and in word form.
Type below:
_________
Answer:
\(\frac{3}{10}\) = 0.3 = three tenths
Explanation:
There are 10 sports balls in the equipment closet. Three are kickballs. So, 3/10 kickballs are available.
Question 11.
Peyton has 2 pizzas. Each pizza is cut into 10 equal slices. She and her friends eat 14 slices. What part of the pizzas did they eat? Write your answer as a decimal.
_________
Answer:
1.4 pizzas
Explanation:
Peyton has 2 pizzas. Each pizza is cut into 10 equal slices.
So, total number of slices = 2 x 10 = 20.
She and her friends eat 14 slices.
So, they ate 1 whole pizza and 4 parts out of 10 slices in the second pizza.
1 4/10 = 14/10 = 1.4 pizzas
Common Core – New – Page No. 500
Lesson Check
Question 1.
Valerie has 10 CDs in her music case. Seven of the CDs are pop music CDs. What is this amount written as a decimal?
Options:
a. 70.0
b. 7.0
c. 0.7
d. 0.07
Answer:
c. 0.7
Explanation:
Valerie has 10 CDs in her music case. Seven of the CDs are pop music CDs.
Seven CDs out of 10 CDs = 7/10 =0.7
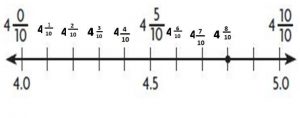
Question 2.
Which decimal amount is modeled below?
Options:
a. 140.0
b. 14.0
c. 1.4
d. 0.14
Answer:
c. 1.4
Explanation:
1\(\frac{4}{10}\)
Multiply 10 x 1 = 10.
Add 10 + 4 = 14.
So, 14/10 = 1.4.
Spiral Review
Question 3.
Which number is a factor of 13?
Options:
a. 1
b. 3
c. 4
d. 7
Answer:
a. 1
Explanation:
13 has 1 and 13 as its factors.
Question 4.
An art gallery has 18 paintings and 4 photographs displayed in equal rows on a wall, with the same number of each type of art in each row. Which of the following could be the number of rows?
Options:
a. 2 rows
b. 3 rows
c. 4 rows
d. 6 rows
Answer:
a. 2 rows
Explanation:
An art gallery has 18 paintings and 4 photographs displayed in equal rows on a wall, with the same number of each type of art in each row. So, 18 paintings and 4 photographs need to be divided into equal parts.
18/2 = 9; 4/2 = 2.
2 rows can be possible with 9 pictures and 2 pictures in each row.
Question 5.
How do you write the mixed number shown as a fraction greater than 1?
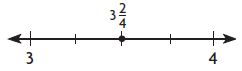
Options:
a. \(\frac{32}{5}\)
b. \(\frac{14}{4}\)
c. \(\frac{6}{4}\)
d. \(\frac{4}{4}\)
Answer:
b. \(\frac{14}{4}\)
Explanation:
3\(\frac{2}{4}\) = 14/4. 14 divided by 4 is equal to 3 with a remainder of 2. The 3 is greater than 1. So, 14/4 > 1.
Question 6.
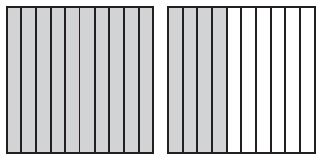
Which of the following models has an amount shaded that is equivalent to the fraction \(\frac{1}{5}\)?
a. ![]()
b. 
c. 
d. 
Answer:
c. 
Explanation:
a. \(\frac{2}{3}\)
b. \(\frac{5}{10}\) = \(\frac{1}{2}\)
c. \(\frac{2}{10}\) = \(\frac{1}{5}\)
d. \(\frac{1}{10}\)
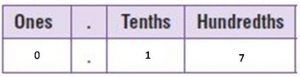
Page No. 503
Question 1.
Shade the model to show \(\frac{31}{100}\).
Write the amount as a decimal.

_____
Answer:
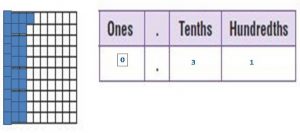
Write the fraction or mixed number and the decimal shown by the model.
Question 2.

Type below:
_________
Answer:
\(\frac{68}{100}\) = 0.68
Explanation:
68 boxes are shaded out of 100 boxes.
Question 3.

Type below:
_________
Answer:
\(\frac{8}{100}\) = 0.08
Explanation:
8 boxes are shaded out of 100 boxes.
Question 4.
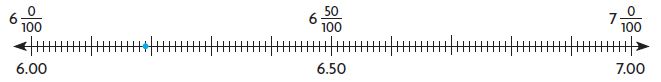
Type below:
_________
Answer:
6\(\frac{19}{100}\) = 6.19
Explanation:
0.5 is 5 tenths and 0.50 is 5 tenths 0 hundredths. Since both 0.5 and 0.50 have 5 tenths and no hundredths, they are equivalent
Write the fraction or mixed number and the decimal shown by the model.
Question 5.
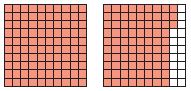
Type below:
_________
Answer:
1\(\frac{83}{100}\) = 1.83
Explanation:
1 whole number(all the square boxes are shaded) and 83 squares boxes shaded out from 100 boxes.
Question 6.

Type below:
_________
Answer:
\(\frac{75}{100}\)
Explanation:
75 boxes are shaded out of 100 boxes.
Question 7.
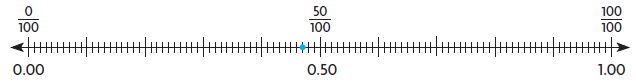
Type below:
_________
Answer:
\(\frac{47}{100}\) = 0.47
Explanation:
The point lies between \(\frac{40}{100}\) and \(\frac{50}{100}\). The number of lines in between \(\frac{40}{100}\) and \(\frac{50}{100}\) are 10. The point is placed at 7th line. So, 40 + 7 = 47. Answer = \(\frac{47}{100}\)
Practice: Copy and Solve Write the fraction or mixed number as a decimal.
Question 8.
\(\frac{9}{100}\) = _____
Answer:
0.09
Explanation:
Write down 9 with the decimal point 2 spaces from the right (because 100 has 2 zeros)
Question 9.
4 \(\frac{55}{100}\) = _____
Answer:
4.55
Explanation:
4 \(\frac{55}{100}\) = \(\frac{455}{100}\)
Write down 455 with the decimal point 2 spaces from the right (because 100 has 2 zeros). So, 4.55 is the answer
Question 10.
\(\frac{10}{100}\) = _____
Answer:
0.10 = 0.1
Explanation:
Write down 10 with the decimal point 2 spaces from the right (because 100 has 2 zeros). So, 0.10 =0.1 is the answer
Question 11.
9 \(\frac{33}{100}\) = _____
Answer:
9.33
Explanation:
9 \(\frac{33}{100}\) = \(\frac{933}{100}\)
Write down 933 with the decimal point 2 spaces from the right (because 100 has 2 zeros). So, 9.33 is the answer.
Question 12.
\(\frac{92}{100}\) = _____
Answer:
0.92
Explanation:
Write down 92 with the decimal point 2 spaces from the right (because 100 has 2 zeros). So, 0.92 is the answer
Question 13.
14 \(\frac{16}{100}\) = _____
Answer:
14.16
Explanation:
14 \(\frac{16}{100}\) = \(\frac{1416}{100}\)
Write down 1416 with the decimal point 2 spaces from the right (because 100 has 2 zeros). So, 14.16 is the answer.
Page No. 504
Question 14.
Shade the grids to show three different ways to represent \(\frac{16}{100}\) using models.

Type below:
_________
Answer:

Question 15.
Describe Relationships Describe how one whole, one tenth, and one hundredth are related.
Type below:
_________
Answer:
One whole = 1.00
One tenth: 0.1
One hundredth: 0.01
One whole is 10 times the one-tenth, and one-tenth is 10 times the one hundredth.
Question 16.
Shade the model to show 1 \(\frac{24}{100}\). Then write the mixed number in decimal form.
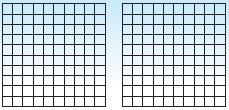
_____
Answer:
1\(\frac{24}{100}\) = \(\frac{124}{100}\) = 1.24
Question 17.
The Memorial Library is 0.3 mile from school. Whose statement makes sense? Whose statement is nonsense? Explain your reasoning.

Type below:
_________
Answer:
The boy’s statement makes sense. Because The Memorial Library is 0.3 miles from the school. Digit 3 in the tenths place after the first place of decimal.
The girl’s statement makes non-sense. Because there she said 3 miles that is not equal to 0.3 miles.
Common Core – New – Page No. 505
Relate Hundredths and Decimals
Write the fraction or mixed number and the decimal shown by the model.
Question 1.
Answer:

Question 2.

Type below:
_________
Answer:
\(\frac{29}{100}\) = 0.29
Explanation:
0.20 names the same amount as 20/100. So, the given point is at 29/100 = 0.29
Question 3.

Type below:
_________
Answer:
1\(\frac{54}{100}\) = 1.54
Explanation:
From the given image, one model is one whole and another model 54 boxes shaded out of 100. So, the answer is 1\(\frac{54}{100}\) = 1.54
Question 4.

Type below:
_________
Answer:
4\(\frac{62}{100}\) = 4.62
Explanation:
4.60 names the same amount as 4\(\frac{60}{100}\). So, the given point is at 4\(\frac{62}{100}\) = 4.62
Write the fraction or mixed number as a decimal.
Question 5.
\(\frac{37}{100}\)
_____
Answer:
0.37
Explanation:
Write down 37 with the decimal point 2 spaces from the right (because 100 has 2 zeros). 0.37
Question 6.
8 \(\frac{11}{100}\)
_____
Answer:
8.11
Explanation:
8\(\frac{11}{100}\) = \(\frac{811}{100}\)
Write down 811 with the decimal point 2 spaces from the right (because 100 has 2 zeros). So, 8.11 is the answer.
Question 7.
\(\frac{98}{100}\)
_____
Answer:
0.98
Explanation:
Write down 98 with the decimal point 2 spaces from the right (because 100 has 2 zeros). 0.98
Question 8.
25 \(\frac{50}{100}\)
_____
Answer:
25.50
Explanation:
25\(\frac{50}{100}\) = \(\frac{2550}{100}\)
Write down 2550 with the decimal point 2 spaces from the right (because 100 has 2 zeros). So, 25.50 is the answer.
Question 9.
\(\frac{6}{100}\)
_____
Answer:
0.06
Explanation:
Write down 6 with the decimal point 2 spaces from the right (because 100 has 2 zeros). 0.06
Problem Solving
Question 10.
There are 100 pennies in a dollar. What fraction of a dollar is 61 pennies? Write it as a fraction, as a decimal, and in word form.
Type below:
_________
Answer:
\(\frac{61}{100}\) pennies = 0.61 = sixty-one hundredths
Explanation:
There are 100 pennies in a dollar. So, for 61 pennies, there are \(\frac{61}{100}\) pennies = 0.61 = sixty-one hundredths.
Question 11.
Kylee has collected 100 souvenir thimbles from different places she has visited with her family. Twenty of the thimbles are carved from wood. Write the fraction of thimbles that are wooden as a decimal.
_________
Answer:
It is easier to work with decimals then fractions because it is like adding whole numbers in a normal way.
Common Core – New – Page No. 506
Lesson Check
Question 1.
Which decimal represents the shaded section of the model below?

Options:
a. 830.0
b. 83.0
c. 8.30
d. 0.83
Answer:
d. 0.83
Explanation:
The model is divided into 100 equal parts. Each part represents one hundredth. 83 boxes are shaded out of 100. So, the answer is \(\frac{83}{100}\) = 0.83
Question 2.
There were 100 questions on the unit test. Alondra answered 97 of the questions correctly. What decimal represents the fraction of questions Alondra answered correctly?
Options:
a. 0.97
b. 9.70
c. 90.70
d. 970.0
Answer:
a. 0.97
Explanation:
There were 100 questions on the unit test. Alondra answered 97 of the questions correctly. So, \(\frac{97}{100}\) questions answered correctly. = 0.97
Spiral Review
Question 3.
Which is equivalent to \(\frac{7}{8}\)?
Options:
a. \(\frac{5}{8}+\frac{3}{8}\)
b. \(\frac{4}{8}+\frac{1}{8}+\frac{1}{8}\)
c. \(\frac{3}{8}+\frac{2}{8}+\frac{2}{8}\)
d. \(\frac{2}{8}+\frac{2}{8}+\frac{1}{8}+\frac{1}{8}\)
Answer:
c. \(\frac{3}{8}+\frac{2}{8}+\frac{2}{8}\)
Explanation:
c. \(\frac{3}{8}+\frac{2}{8}+\frac{2}{8}\) = \(\frac{7}{8}\)
Question 4.
What is \(\frac{9}{10}-\frac{6}{10}\)?

Options:
a. \(\frac{1}{10}\)
b. \(\frac{3}{10}\)
c. \(\frac{4}{10}\)
d. \(\frac{6}{10}\)
Answer:
b. \(\frac{3}{10}\)
Explanation:
\(\frac{9}{10}-\frac{6}{10}\). From 9 parts, 6 parts are removed. So, remaining parts are 3.
Question 5.
Misha used \(\frac{1}{4}\) of a carton of 12 eggs to make an omelet. How many eggs did she use?
Options:
a. 2
b. 3
c. 4
d. 6
Answer:
b. 3
Explanation:
Misha used \(\frac{1}{4}\) of a carton of 12 eggs to make an omelet. \(\frac{1}{4}\) x 12 = 3 eggs.
Question 6.
Kurt used the rule add 4, subtract 1 to generate a pattern. The first term in his pattern is 5. Which number could be in Kurt’s pattern?
Options:
a. 4
b. 6
c. 10
d. 14
Answer:
d. 14
Explanation:
Kurt used the rule add 4, subtract 1 to generate a pattern. The first term in his pattern is 5. The pattern numbers are 5, 8, 11, 14, 17, 20, etc. So, the answer is 14.
Page No. 509
Question 1.
Write \(\frac{4}{10}\) as hundredths.
Write \(\frac{4}{10}\) as an equivalent fraction.
\(\frac{4}{10}\) =\(\frac{4 × ■}{10× ■}\)
Write \(\frac{4}{10}\) as a decimal.
Type below:
_________
Answer:
\(\frac{40}{100}\)
0.40
Explanation:
Write \(\frac{4}{10}\) as an equivalent fraction.
\(\frac{4}{10}\) =\(\frac{4 × 10}{10× 10}\) = \(\frac{40}{100}\)
6 tenths is the same as 6 tenths 0 hundredths. So the decimal form = 0.40
Write the number as hundredths in fraction form and decimal form.
Question 2.
\(\frac{7}{10}\)
Type below:
_________
Answer:
\(\frac{70}{100}\)
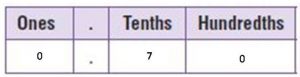
0.70
Explanation:
Write \(\frac{7}{10}\) as an equivalent fraction.
\(\frac{7}{10}\) =\(\frac{7 × 10}{10× 10}\) = \(\frac{70}{100}\)
7 tenths is the same as 7 tenths 0 hundredths. So the decimal form = 0.70
Question 3.
0.5
Type below:
_________
Answer:
\(\frac{50}{100}\)
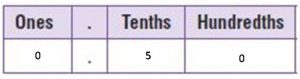
0.50
Explanation:
Write 0.5 = \(\frac{5}{10}\) as an equivalent fraction.
\(\frac{5}{10}\) =\(\frac{5 × 10}{10× 10}\) = \(\frac{50}{100}\)
5 tenths is the same as 5 tenths 0 hundredths and also 0.5
Question 4.
\(\frac{3}{10}\)
Type below:
_________
Answer:
\(\frac{30}{100}\)
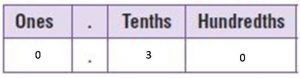
0.30
Explanation:
Write \(\frac{3}{10}\) as an equivalent fraction.
\(\frac{3}{10}\) =\(\frac{3 × 10}{10× 10}\) = \(\frac{30}{100}\)
3 tenths is the same as 3 tenths 0 hundredths. So the decimal form = 0.30
Write the number as tenths in fraction form and decimal form.
Question 5.
0.40
Type below:
_________
Answer:
\(\frac{4}{10}\) = 0.4
Explanation:

There are no hundredths.
0.40 is equivalent to 4 tenths.
Write 0.40 as 4 tenths = 0.4 = \(\frac{4}{10}\)
Question 6.
\(\frac{80}{100}\)
Type below:
_________
Answer:
\(\frac{8}{10}\)
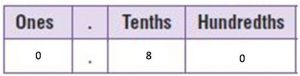
0.8
Explanation:
10 is a common factor of the numerator and the denominator.
\(\frac{80}{100}\) = \(\frac{80 ÷ 10}{100 ÷ 10}\) = \(\frac{8}{10}\)
0.8
Question 7.
\(\frac{20}{100}\)
Type below:
_________
Answer:
\(\frac{2}{10}\)
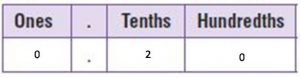
0.2
Explanation:
10 is a common factor of the numerator and the denominator.
\(\frac{20}{100}\) = \(\frac{20 ÷ 10}{100 ÷ 10}\) = \(\frac{2}{10}\)
0.2
Practice: Copy and Solve Write the number as hundredths in fraction form and decimal form.
Question 8.
\(\frac{8}{10}\)
Type below:
_________
Answer:
\(\frac{80}{100}\)

0.8
Explanation:
Write \(\frac{8}{10}\) as an equivalent fraction.
\(\frac{8}{10}\) =\(\frac{8 × 10}{10× 10}\) = \(\frac{80}{100}\)
8 tenths is the same as 8 tenths 0 hundredths. So the decimal form = 0.8
Question 9.
\(\frac{2}{10}\)
Type below:
_________
Answer:
\(\frac{20}{100}\)

0.2
Explanation:
Write \(\frac{2}{10}\) as an equivalent fraction.
\(\frac{2}{10}\) =\(\frac{2 × 10}{10× 10}\) = \(\frac{20}{100}\)
2 tenths is the same as 2 tenths 0 hundredths. So the decimal form = 0.2
Question 10.
0.1
Type below:
_________
Answer:
\(\frac{50}{100}\)
![]()
0.50
Explanation:
Write 0.1 = \(\frac{1}{10}\) as an equivalent fraction.
\(\frac{1}{10}\) =\(\frac{1 × 10}{10× 10}\) = \(\frac{10}{100}\)
1 tenth is the same as 1 tenth 0 hundredths and also 0.1
Practice: Copy and Solve Write the number as tenths in fraction form and decimal form.
Question 11.
\(\frac{60}{100}\)
Type below:
_________
Answer:
\(\frac{6}{10}\)
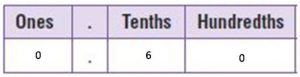
0.6
Explanation:
10 is a common factor of the numerator and the denominator.
\(\frac{60}{100}\) = \(\frac{60 ÷ 10}{100 ÷ 10}\) = \(\frac{6}{10}\)
0.6
Question 12.
\(\frac{90}{100}\)
Type below:
_________
Answer:
\(\frac{9}{10}\)
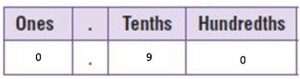
0.9
Explanation:
10 is a common factor of the numerator and the denominator.
\(\frac{90}{100}\) = \(\frac{90 ÷ 10}{100 ÷ 10}\) = \(\frac{9}{10}\)
= 0.9
Question 13.
0.70
Type below:
_________
Answer:
\(\frac{7}{10}\)

0.7
Explanation:

There are no hundredths.
0.70 is equivalent to 7 tenths.
Write 0.70 as 7 tenths = 0.7 = \(\frac{7}{10}\)
Write the number as an equivalent mixed number with hundredths.
Question 14.
1 \(\frac{4}{10}\) = _____
Answer:
1 \(\frac{40}{100}\)
Explanation:
1 \(\frac{4 x 10}{10 x 10}\) = 1 \(\frac{40}{100}\)
Question 15.
3 \(\frac{5}{10}\) = _____
Answer:
3 \(\frac{50}{100}\)
Explanation:
3 \(\frac{5}{10}\) = 3 \(\frac{5 x 10}{10 x 10}\) = 3 \(\frac{50}{100}\)
Question 16.
2 \(\frac{9}{10}\) = _____
Answer:
2 \(\frac{90}{100}\)
Explanation:
2 \(\frac{9}{10}\) = 2 \(\frac{9 x 10}{10 x 10}\) = 2 \(\frac{90}{100}\)
Page No. 510
Question 17.
Carter says that 0.08 is equivalent to \(\frac{8}{10}\). Describe and correct Carter’s error.
Type below:
_________
Answer:
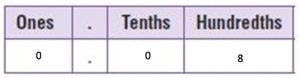
8 hundredths = \(\frac{8}{100}\)
The decimal point is before the 2 numbers. So, the denominator should be 100.
Question 18.
For numbers 18a–18e, choose True or False for the statement.
a. 0.6 is equivalent to \(\frac{6}{100}\).
i. True
ii. False
Answer:
ii. False
Explanation:

0.60 = 6 tenths.
6 tenths = \(\frac{6}{10}\)
Question 18.
b. \(\frac{3}{10}\) is equivalent to 0.30.
i. True
ii. False
Answer:
i. True
Explanation:

0.30 = 3 tenths.
3 tenths = \(\frac{3}{10}\)
Question 18.
c. \(\frac{40}{100}\) is equivalent to \(\frac{4}{10}\).
i. True
ii. False
Answer:
i. True
Explanation:
10 is a common factor of the numerator and the denominator.
\(\frac{40}{100}\) = \(\frac{40 ÷ 10}{100 ÷ 10}\) = \(\frac{4}{10}\)
Question 18.
d. 0.40 is equivalent to \(\frac{4}{100}\).
i. True
ii. False
Answer:
ii. False
Explanation:

4 tenths and 0 hundreds = \(\frac{4}{10}\)
Question 18.
e. 0.5 is equivalent to 0.50.
i. True
ii. False
Answer:
i. True
Explanation:
If you add any zeros after the 5 it will be equal to 0.5. So, 0.5 is equivalent to 0.50
Inland Water
How many lakes and rivers does your state have? The U.S. Geological Survey defines inland water as water that is surrounded by land. The Atlantic Ocean, the Pacific Ocean, and the Great Lakes are not considered inland water.

Question 19.
Just over \(\frac{2}{100}\) of the entire United States is inland water. Write \(\frac{2}{100}\) as a decimal.
_____
Answer:
0.02
Explanation:
Write down 2 with the decimal point 2 spaces from the right (because 100 has 2 zeros). So, \(\frac{2}{100}\) = 0.02 is the answer
Question 20.
Can you write 0.02 as tenths? Explain.
_____ tenth
Answer:
0.2 tenth
Explanation:
0.02 = \(\frac{2}{100}\) = \(\frac{2 ÷ 10}{100 ÷ 10}\) = \(\frac{0.2}{10}\)
Question 21.
About 0.17 of the area of Rhode Island is inland water. Write 0.17 as a fraction.
\(\frac{□}{□}\)
Answer:
\(\frac{17}{100}\)
Explanation:
1 tenth and 7 hundred.
So, write 0.17 as \(\frac{17}{100}\)
Question 22.
Louisiana’s lakes and rivers cover about \(\frac{1}{10}\) of the state. Write \(\frac{1}{10}\) as hundredths in words, fraction form, and decimal form.
Type below:
_________
Answer:
Ten hundredths = \(\frac{10}{100}\) = 0.10
Explanation:
1 tenth is the same as the 1 tenth and 0 hundred
![]()
0.1 = 0.10 = \(\frac{10}{100}\)
Common Core – New – Page No. 511
Equivalent Fractions and Decimals
Write the number as hundredths in fraction form and decimal form.
Question 1.
\(\frac{5}{10}\) \(\frac{5}{10}\) = \(\frac{5 \times 10}{10 \times 10}\) = \(\frac{50}{100}\)
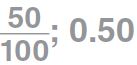
Think: 5 tenths is the same as 5 tenths and 0 hundredths. Write 0.50.
Question 2.
\(\frac{9}{10}\)
Type below:
_________
Answer:
\(\frac{90}{100}\); 0.90
Explanation:
\(\frac{9}{10}\) = \(\frac{9 \times 10}{10 \times 10}\) = \(\frac{90}{100}\)
9 tenths is the same as 9 tenths and 0 hundredths. Write 0.90
Question 3.
0.2
Type below:
_________
Answer:
\(\frac{20}{100}\)
0.20
Explanation:
2 tenths is the same as 2 tenths and 0 hundredths. Write 0.20.

\(\frac{2}{10}\) = \(\frac{2 x 10}{10 x 10}\) = \(\frac{20}{100}\)
Question 4.
0.8
Type below:
_________
Answer:
\(\frac{80}{100}\) = 0.80
Explanation:
8 tenths is the same as 8 tenths and 0 hundredths. Write 0.80.

\(\frac{8}{10}\) = \(\frac{8 x 10}{10 x 10}\) = \(\frac{80}{100}\)
Write the number as tenths in fraction form and decimal form.
Question 5.
\(\frac{40}{100}\)
Type below:
_________
Answer:
\(\frac{4}{10}\) = 0.4
Explanation:
10 is a common factor of the numerator and the denominator.
\(\frac{40}{100}\) = \(\frac{40 ÷ 10}{100 ÷ 10}\) = \(\frac{4}{10}\)
= 0.4
Question 6.
\(\frac{10}{100}\)
Type below:
_________
Answer:
\(\frac{1}{10}\) = 0.1
Explanation:
10 is a common factor of the numerator and the denominator.
\(\frac{10}{100}\) = \(\frac{10 ÷ 10}{100 ÷ 10}\) = \(\frac{1}{10}\)
= 0.1
Question 7.
0.60
Type below:
_________
Answer:
\(\frac{6}{10}\) = 0.6
Explanation:
0.60 is 60 hundredths.
\(\frac{60}{100}\).
10 is a common factor of the numerator and the denominator.
\(\frac{60}{100}\) = \(\frac{60 ÷ 10}{100 ÷ 10}\) = \(\frac{6}{10}\)
= 0.6
Problem Solving
Question 8.
Billy walks \(\frac{6}{10}\) mile to school each day. Write \(\frac{6}{10}\) as hundredths in fraction form and in decimal form.
Type below:
________
Answer:
\(\frac{60}{100}\)
0.60
Explanation:
Billy walks \(\frac{6}{10}\) mile to school each day.
\(\frac{6}{10}\) = \(\frac{6 x 10}{10 x 10}\) = \(\frac{60}{100}\)

0.60
Question 9.
Four states have names that begin with the letter A. This represents 0.08 of all the states. Write 0.08 as a fraction.
\(\frac{□}{□}\)
Answer:
\(\frac{8}{100}\)
Explanation:
0.08 is 8 hundredths. So, the fraction is \(\frac{8}{100}\)
Common Core – New – Page No. 512
Lesson Check
Question 1.
The fourth-grade students at Harvest School make up 0.3 of all students at the school. Which fraction is equivalent to 0.3?
Options:
a. \(\frac{3}{10}\)
b. \(\frac{30}{10}\)
c. \(\frac{3}{100}\)
d. \(\frac{33}{100}\)
Answer:
a. \(\frac{3}{10}\)
Explanation:
0.3 is same as the 3 tenths. So, the answer is \(\frac{3}{10}\)
Question 2.
Kyle and his brother have a marble set. Of the marbles, 12 are blue. This represents \(\frac{50}{100}\) of all the marbles. Which decimal is equivalent to \(\frac{50}{100}\)?
Options:
a. 50
b. 5.0
c. 0.50
d. 5,000
Answer:
c. 0.50
Explanation:
Write down 50 with the decimal point 2 spaces from the right (because 100 has 2 zeros). So, 0.50 is the answer
Spiral Review
Question 3.
Jesse won his race by 3 \(\frac{45}{100}\) seconds. What is this number written as a decimal?
Options:
a. 0.345
b. 3.45
c. 34.5
d. 345
Answer:
b. 3.45
Explanation:
3 \(\frac{45}{100}\) = \(\frac{345}{100}\). Write down 345 with the decimal point 2 spaces from the right (because 100 has 2 zeros). So, 3.45 is the answer
Question 4.
Marge cut 16 pieces of tape for mounting pictures on poster board. Each piece of tape was \(\frac{3}{8}\) inch long. How much tape did Marge use?
Options:
a. 2 inches
b. 4 inches
c. 5 inches
d. 6 inches
Answer:
d. 6 inches
Explanation:
\(\frac{3}{8}\) x 16 = 6 inches
Question 5.
Of Katie’s pattern blocks, \(\frac{9}{12}\) are triangles. What is \(\frac{9}{12}\) in simplest form?
Options:
a. \(\frac{1}{4}\)
b. \(\frac{2}{3}\)
c. \(\frac{3}{4}\)
d. \(\frac{9}{12}\)
Answer:
c. \(\frac{3}{4}\)
Explanation:
\(\frac{9}{12}\) is divided by 3. So, \(\frac{3}{4}\) is the answer.
Question 6.
A number pattern has 75 as its first term. The rule for the pattern is subtract 6. What is the sixth term?
Options:
a. 39
b. 45
c. 51
d. 69
Answer:
b. 45
Explanation:
75 is the first term.
75 – 6 =69
69 – 6 = 63
63 – 6 = 57
57 – 6 = 51
51 – 6 = 45.
The sixth term is 45.
Page No. 515
Question 1.
Write the amount of money as a decimal in terms of dollars.
![]()
5 pennies = \(\frac{5}{100}\) of a dollar = _____ of a dollar.
_____ of a dollar
Answer:
5 pennies = \(\frac{5}{100}\) of a dollar = 0.05 of a dollar.
0.05 of a dollar
Explanation:
Write down 5 with the decimal point 2 spaces from the right (because 100 has 2 zeros). 0.05
Write the total money amount. Then write the amount as a fraction or a mixed number and as a decimal in terms of dollars.
Question 2.

Type below:
_________
Answer:
\(\frac{109}{100}\) = 1.09
Explanation:
1 dollar = 1/10 dimes
1 dollar = 1/100 pennies
1 dollar = 25/100 quarters
(3 x 1/10) + (4 x 1/100) + (3 x 25/100)
3/10 + 4/100 + 75/100
30/100 + 4/100 + 75/100 = 109/100 = 1.09
Question 3.

Type below:
_________
Answer:
\(\frac{60}{100}\) = 0.60
Explanation:
Given that 1 quarter, 2 dimes, and 3 cents.
10 dimes = 1 dollars
100 pennies = 1 dollar
4 quarters = 1 dollar
2 cents = 1 dollar
(25/100) + (2 x 1/10) + (3 x 5/100) = 25/100 + 20/100 + 15/100 = 60/100 = 0.60
Write as a money amount and as a decimal in terms of dollars.
Question 4.
\(\frac{92}{100}\)
amount: _____ decimal: _____of a dollar
Answer:
amount: $0.92 decimal: 0.92 of a dollar
Explanation:
\(\frac{92}{100}\) = 0.92
Question 5.
\(\frac{7}{100}\)
money amount: $ _____ decimal: _____ of a dollar
Answer:
money amount: $0.07 decimal: 0.07 of a dollar
Explanation:
\(\frac{7}{100}\) = 0.07
Question 6.
\(\frac{16}{100}\)
money amount: $ _____ decimal: _____ of a dollar
Answer:
money amount: $0.16 decimal: 0.16 of a dollar
Explanation:
\(\frac{16}{100}\) = 0.16
Question 7.
\(\frac{53}{100}\)
money amount: $ _____ decimal: _____ of a dollar
Answer:
money amount: $0.53 decimal: 0.53 of a dollar
Explanation:
\(\frac{53}{100}\) = 0.53
Write the total money amount. Then write the amount as a fraction or a mixed number and as a decimal in terms of dollars.
Question 8.

Type below:
_________
Answer:
\(\frac{46}{100}\) = 0.46
Explanation:
Given that 3 dimes, 3 nickels, 1 pennies
(3 x 10/100) + (3 x 5/100) + 1/100 = 30/100 + 15/100 + 1/100 = 46/100 = 0.46
Question 9.

Type below:
_________
Answer:
\(\frac{136}{100}\) = 1.36
Explanation:
Given that 1 dollar, 1 quarter, 1 pennies, 2 nickels
1 + 25/100 + 1/100 + (2 x 5/100)
1 + 25/100 + 1/100 + 10/100
1 + 36/100
136/100 = 1.36
Write as a money amount and as a decimal in terms of dollars.
Question 10.
\(\frac{27}{100}\)
money amount: $ _____ decimal: _____ of a dollar
Answer:
amount: $0.27 decimal: 0.27 of a dollar
Explanation:
\(\frac{27}{100}\) = 0.27
Question 11.
\(\frac{4}{100}\)
money amount: $ _____ decimal: _____ of a dollar
Answer:
amount: $0.04 decimal: 0.04 of a dollar
Explanation:
\(\frac{4}{100}\) = 0.04
Question 12.
\(\frac{75}{100}\)
money amount: $ _____ decimal: _____ of a dollar
Answer:
amount: $0.75 decimal: 0.75 of a dollar
Explanation:
\(\frac{75}{100}\) = 0.75
Question 13.
\(\frac{100}{100}\)
money amount: $ _____ decimal:_____ of a dollar
Answer:
money amount: $1 decimal: 1 of a dollar
Explanation:
\(\frac{100}{100}\) = 1
Write the total money amount. Then write the amount as a fraction and as a decimal in terms of dollars.
Question 14.
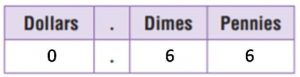
1 quarter 6 dimes 8 pennies
Type below:
_________
Answer:
money amount: $0.39; fraction: \(\frac{39}{100}\) decimal: 0.39 of a dollar
Explanation:
1 dollar = 100 cents
1 quarter = 25 cents
1 dime = 10 cents
1 penny = 1 cent
1 quarter 6 dimes 8 pennies = (25/100) + (6 x 10/100) + (8 x 1/100)
25/100 + 60/100 + 8/100 = 39/100 = 0.39
Question 15.
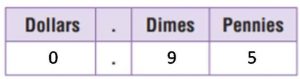
3 dimes 5 nickels 20 pennies
Type below:
_________
Answer:
money amount: $0.75; fraction: \(\frac{75}{100}\) decimal: 0.75 of a dollar
Explanation:
1 dollar = 100 cents
1 quarter = 25 cents
1 dime = 10 cents
1 penny = 1 cent
3 dimes 5 nickels 20 pennies = (3 x 10/100) + (5 x 5/100) + (20 x 1/100)
30/100 + 25/100 + 20/100 = 75/100 = 0.75
Page No. 516
Make Connections Algebra Complete to tell the value of each digit.
Question 16.
a.
$1.05 = _____ dollar + _____ pennies;
Answer:
$1.05 = 1 dollar + 5 pennies
Explanation:
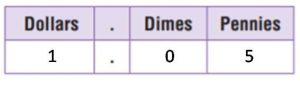
$1.05 = 1 dollar and 05 pennies
There are 100 pennies in 1 dollar.
So, $1.05 = 105 pennies.
Question 16.
b.
1.05 = _____ one + _____ hundredths
Answer:
1.05 = 1 one and 05 hundredths
Explanation:
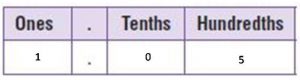
1.05 = 1 one and 05 hundredths
There are 100 hundredths in 1 one.
So, 1.05 = 105 hundredths.
Question 17.
a.
$5.18 = _____ dollars + _____ dime + _____ pennies;
Answer:
$5.18 = 5 dollars + 1 dime + 8 pennies;
Explanation:
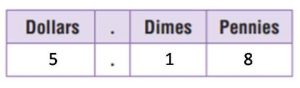
$5.18 = 5 dollar and 1 dime and 8 pennies
There are 500 pennies in 5 dollars.
1 dime = 10 pennies
So, $5.18 = 518 pennies.
Question 17.
b.
5.18 = _____ ones + _____ tenth + _____ pennies
Answer:
5.18 = 5 ones + 1 tenths + 8 pennies
Explanation:
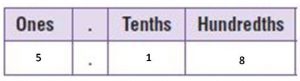
5.18 = 5 ones and 1 tenths and 8 pennies
There are 100 hundredths in 1 one. So, 500 hundredths in 5 ones.
So, 5.18 = 518 hundredths.
Use the table for 18–19.
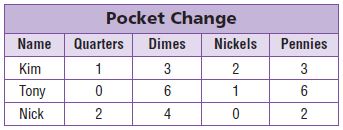
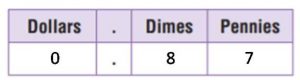
Question 18.
The table shows the coins three students have. Write Nick’s total amount as a fraction in terms of dollars.
\(\frac{□}{□}\) of a dollar
Answer:
\(\frac{92}{100}\) of a dollar
Explanation:
Nick’s total amount = 2 quarters + 4 dimes + 0 Nickels + 2 pennies
= (2 x 25/100) + (4 x 10/100) + (2 x 1/100) = 50/100 + 40/100 + 2/100 = 92/100
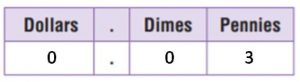
Question 19.
Kim spent \(\frac{40}{100}\) of a dollar on a snack. Write as a money amount the amount she has left.
$ _____
Answer:
$0.28
Explanation:
Kim’s total amount = 1 quarter + 3 dimes + 2 nickels + 3 pennies
= 25/100 + (3 x 10/100) + (2 x 5/100) + (3 x 1/100) = 25/100 + 30/100 + 10/100 + 3/100 = 68/100.
Kim spent \(\frac{40}{100}\) of a dollar on a snack. So, 68/100 – 40/100 = 28/100 = 0.28
Question 20.
Travis has \(\frac{1}{2}\) of a dollar. He has at least two different types of coins in his pocket. Draw two possible sets of coins that Travis could have.
Type below:
_________
Answer:
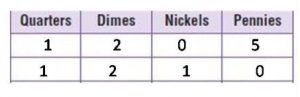
Explanation:
1 Quarter + 2 dimes + 5 Pennies = 25/100 + 10/100 + 10/100 + 5/100 = 50/100 = 1/2 of a dollar
1 Quarter + 2 dimes + 1 Nickel = 25/100 + 10/100 + 10/100 + 5/100 = 50/100 = 1/2 of a dollar
Question 21.
Complete the table.
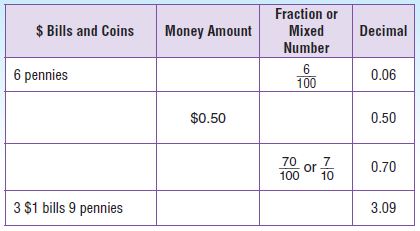
Type below:
_________
Answer:
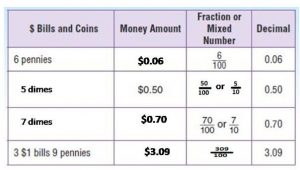
Common Core – New – Page No. 517
Relate Fractions, Decimals, and Money
Write the total money amount. Then write the amount as a fraction or a mixed number and as a decimal in terms of dollars.
Question 1.

Answer:
$0.18 = \(\frac{18}{100}\) = 0.18
Explanation:
Given that 3 Pennies + 3 Nickels = 3/100 + 15/100 = 18/100
Question 2.

Type below:
_________
Answer:
$0.56 = \(\frac{56}{100}\) = 0.56
Explanation:
Given that 1 Quarter + 3 dime + 1 Pennies = 25/100 + 30/100 + 1/100 = 56/100
Write as a money amount and as a decimal in terms of dollars.
Question 3.
\(\frac{25}{100}\)
Dollars: _____ Decimal: _____
Answer:
Dollars: 1 quarter = $0.25; Decimal: 0.25
Explanation:
25 our of 100 dollars = 1 quarter.
So, 25/100 = 0.25
Question 4.
\(\frac{79}{100}\)
Dollars: _____ Decimal: _____
Answer:
amount: $0.79 decimal: 0.79 of a dollar
Explanation:
\(\frac{79}{100}\) = 0.79
Question 5.
\(\frac{31}{100}\)
Dollars: _____ Decimal: _____
Answer:
amount: $0.31 decimal: 0.31 of a dollar
Explanation:
\(\frac{31}{100}\) = 0.31
Question 6.
\(\frac{8}{100}\)
Dollars: _____ Decimal: _____
Answer:
amount: $0.08 decimal: 0.08 of a dollar
Explanation:
\(\frac{8}{100}\) = 0.08
Question 7.
\(\frac{42}{100}\)
Dollars: _____ Decimal: _____
Answer:
amount: $0.42 decimal: 0.42 of a dollar
Explanation:
\(\frac{42}{100}\) = 0.42
Write the money amount as a fraction in terms of dollars.
Question 8.
$0.87
\(\frac{□}{□}\)
Answer:
\(\frac{87}{100}\) of a dollar
Explanation:
$0.87 = 87 pennies
There are 100 pennies in 1 dollar.
So, $0.87 = \(\frac{87}{100}\) of a dollar.
Question 9.
$0.03
\(\frac{□}{□}\)
Answer:
\(\frac{3}{100}\)
Explanation:
$0.03 = 3 pennies
There are 100 pennies in 1 dollar.
So, $0.03 = \(\frac{3}{100}\).
Question 10.
$0.66
\(\frac{□}{□}\)
Answer:
\(\frac{66}{100}\)
Explanation:
$0.66 = 66 pennies
There are 100 pennies in 1 dollar.
So, $0.66 = \(\frac{66}{100}\).
Question 11.
$0.95
\(\frac{□}{□}\)
Answer:
\(\frac{95}{100}\)
Explanation:
$0.95 = 95 pennies
There are 100 pennies in 1 dollar.
So, $0.95 = \(\frac{95}{100}\).
Question 12.
$1.00
\(\frac{□}{□}\)
Answer:
\(\frac{100}{100}\)
Explanation:
$1.00 = 1 dollar
There are 100 pennies in 1 dollar.
So, $1.00 = \(\frac{100}{100}\).
Write the total money amount. Then write the amount as a fraction and as a decimal in terms of dollars.
Question 13.
2 quarters 2 dimes
Type below:
_________
Answer:
money amount: $0.70; fraction: \(\frac{70}{100}\); decimal: 0.70
Explanation:
Given that 2 quarters 2 dimes = (2 x 25/100) + (2 x 10/100) = 50/100 + 20/100 = 70/100
Question 14.
3 dimes 4 pennies
Type below:
_________
Answer:
money amount: $0.34; fraction: \(\frac{34}{100}\); decimal: 0.34
Explanation:
Given that 3 dimes 4 pennies = (3 x 10/100) + (4 x 1/100) = 30/100 + 4/100 = 34/100
Question 15.
8 nickels 12 pennies
Type below:
_________
Answer:
money amount: $0.57; fraction: \(\frac{57}{100}\); decimal: 0.57
Explanation:
Given that 8 nickels 12 pennies = (8 x 5/100) + (12 x 1/100) = 45/100 + 12/100 = 57/100
Problem Solving
Question 16.
Kate has 1 dime, 4 nickels, and 8 pennies. Write Kate’s total amount as a fraction in terms of a dollar.
\(\frac{□}{□}\)
Answer:
fraction: \(\frac{38}{100}\)
Explanation:
Kate has 1 dime, 4 nickels, and 8 pennies.
10/100 + (4 x 5/100) + (8/100) = 10/100 + 20/100 + 8/100 = 38/100
Question 17.
Nolan says he has \(\frac{75}{100}\) of a dollar. If he only has 3 coins, what are the coins?
_________
Answer:
3 quarters
Explanation:
3 quarters = \(\frac{25}{100}\) + \(\frac{25}{100}\) + \(\frac{25}{100}\) = \(\frac{75}{100}\)
Common Core – New – Page No. 518
Lesson Check
Question 1.
Which of the following names the total money amount shown as a fraction in terms of a dollar?

Options:
a. \(\frac{43}{1}\)
b. \(\frac{43}{10}\)
c. \(\frac{43}{57}\)
d. \(\frac{43}{100}\)
Answer:
d. \(\frac{43}{100}\)
Explanation:
Given that 1 quarter + 1 nickel + 1 dime + 3 pennies = 25/100 + 5/100 + 10/100 + 3/100 = 43/100
Question 2.
Crystal has \(\frac{81}{100}\) of a dollar. Which of the following could be the coins Crystal has?
Options:
a. 3 quarters, 1 dime, 1 penny
b. 2 quarters, 6 nickels, 1 penny
c. 2 quarters, 21 pennies
d. 1 quarter, 4 dimes, 1 nickel, 1 penny
Answer:
b. 2 quarters, 6 nickels, 1 penny
Explanation:
2 quarters, 6 nickels, 1 penny = (2 x 25/100) + (6 x 5/100) + 1/100 = 50/100 + 30/100 + 1/100 = 81/100
Spiral Review
Question 3.
Joel gives \(\frac{1}{3}\) of his baseball cards to his sister. Which fraction is equivalent to \(\frac{1}{3}\)?
Options:
a. \(\frac{3}{5}\)
b. \(\frac{2}{6}\)
c. \(\frac{8}{9}\)
d. \(\frac{4}{10}\)
Answer:
b. \(\frac{2}{6}\)
Explanation:
\(\frac{2}{6}\) is divided by 2. The remaining answer after the dividion is \(\frac{1}{3}\).
Question 4.
Penelope bakes pretzels. She salts \(\frac{3}{8}\) of the pretzels. Which fraction is equivalent to \(\frac{3}{8}\)?
Options:
a. \(\frac{9}{24}\)
b. \(\frac{15}{20}\)
c. \(\frac{3}{16}\)
d. \(\frac{1}{5}\)
Answer:
a. \(\frac{9}{24}\)
Explanation:
a. \(\frac{9}{24}\) is divided by 3. The remaining fraction after the division is \(\frac{3}{8}\).
Question 5.
Which decimal is shown by the model?

Options:
a. 10.0
b. 1.0
c. 0.1
d. 0.01
Answer:
d. 0.01
Explanation:
1 box is shaded out of 100. So, the fraction is 1/100 = 0.01.
Question 6.
Mr. Guzman has 100 cows on his dairy farm. Of the cows, 57 are Holstein. What decimal represents the portion of cows that are Holstein?
Options:
a. 0.43
b. 0.57
c. 5.7
d. 57.0
Answer:
b. 0.57
Explanation:
Mr. Guzman has 100 cows on his dairy farm. Of the cows, 57 are Holstein. So, 57/100 Holstein cows are available.
57/100 = 0.57
Page No. 521
Question 1.
Juan has $3.43. He is buying a paint brush that costs $1.21 to paint a model race car. How much will Juan have after he pays for the paint brush?
First, use bills and coins to model $3.43.

Next, you need to subtract. Remove bills and coins that have a value of $1.21. Mark Xs to show what you remove.
Last, count the value of the bills and coins that are left. How much will Juan have left?
$ _____
Answer:
Juan has $3.43. He is buying a paint brush that costs $1.21 to paint a model race car. Subtract $3.43 – $1.21

2 dollars, 2 dimes, and 2 pennies left.
2 + (2 x 10/100) + (2/100) = 2 + 20/100 + 2/100 = 2 + 22/100 = 2.22.
Juan has left $2.22
Question 2.
What if Juan has $3.43, and he wants to buy a paint brush that costs $2.28? How much money will Juan have left then? Explain.
$ _____
Answer:
$1.15
Explanation:
Juan has $3.43. He wants to buy a paint brush that costs $2.28.
$3.43 – $2.28 = $1.15
Question 3.
Sophia has $2.25. She wants to give an equal amount to each of her 3 young cousins. How much will each cousin receive?
$ _____ each cousin receive
Answer:
$0.75 each cousin receive
Explanation:
Sophia has $2.25. She wants to give an equal amount to each of her 3 young cousins.
Divide $2.25 with 3 = $2.25/3 = $0.75
Page No. 522
Question 4.
Marcus saves $13 each week. In how many weeks will he have saved at least $100?
_____ weeks
Answer:
8 weeks
Explanation:
Marcus saves $13 each week. He saves $100 in $100/$13 weeks = 7.96 weeks that is nearly equal to 8 weeks.
Question 5.
Analyze Relationships Hoshi has $50. Emily has $23 more than Hoshi. Karl has $16 less than Emily. How much money do they have all together?
$ _____
Answer:
$180
Explanation:
Hoshi has $50.
Emily has $23 more than Hoshi = $50 + $23 = $73.
Karl has $16 less than Emily = $73 – $16 = $57.
All together = $50 +$73 + $57 = $180.
Question 6.
Four girls have $5.00 to share equally. How much money will each girl get? Explain.
$ _____ each girl
Answer:
$1.25 for each girl
Explanation:
Four girls have $5.00 to share equally. So, each girl get $5.00/4 = $1.25
Question 7.
What if four girls want to share $5.52 equally? How much money will each girl get? Explain.
$ _____
Answer:
$1.38
Explanation:
Four girls have $5.52 to share equally. So, each girl get $5.52/4 = $1.38. If the amount shares equally, each girl get 1 dollar, 1 dime, 8 pennies.
Question 8.
Aimee and three of her friends have three quarters and one nickel. If Aimee and her friends share the money equally, how much will each person get? Explain how you found your answer.
$ _____
Answer:
$0.2
Explanation:
Aimee and three of her friends have three quarters and one nickel. If Aimee and her friends share the money equally. Four members shared (3 x 25/100) + 5/100 = 75/100 + 5/100 = 80/100 = 0.8.
Four members shared $0.8 equally, $0.8/4 = $0.2.
Common Core – New – Page No. 523
Problem Solving Money
Use the act it out strategy to solve.
Question 1.
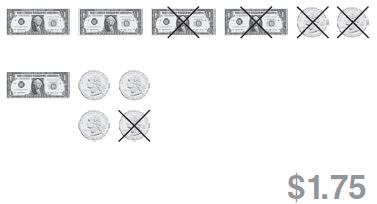
Carl wants to buy a bicycle bell that costs $4.50. Carl has saved $2.75 so far. How much more money does he need to buy the bell?
Use 4 $1 bills and 2 quarters to model $4.50. Remove bills and coins that have a value of $2.75. First, remove 2 $1 bills and 2 quarters.
Next, exchange one $1 bill for 4 quarters and remove 1 quarter.
Count the amount that is left. So, Carl needs to save $1.75 more.
Answer:

Question 2.
Together, Xavier, Yolanda, and Zachary have $4.44. If each person has the same amount, how much money does each person have?
$ __________
Answer:
$1.11
Explanation:
Together, Xavier, Yolanda, and Zachary have $4.44. If each person has the same amount, $4.44/4 = $1.11
Question 3.
Marcus, Nan, and Olive each have $1.65 in their pockets. They decide to combine the money. How much money do they have altogether?
$ __________
Answer:
$4.95
Explanation:
Marcus, Nan, and Olive each have $1.65 in their pockets. They decide to combine the money. So, $1.65 + $1.65 + $1.65 = $4.95
Question 4.
Jessie saves $6 each week. In how many weeks will she have saved at least $50?
__________ weeks
Answer:
9 weeks
Explanation:
Jessie saves $6 each week. To save $50, $50/$6 = 9 weeks (approximately)
Question 5.
Becca has $12 more than Cece. Dave has $3 less than Cece. Cece has $10. How much money do they have altogether?
$ __________
Answer:
$39
Explanation:
Cece has $10.
Becca has $12 more than Cece = $10 + $12 = $22.
Dave has $3 less than Cece = $10 – $3 = $7.
All together = $10 + $22 + $7 = $39.
Common Core – New – Page No. 524
Lesson Check
Question 1.
Four friends earned $5.20 for washing a car. They shared the money equally. How much did each friend get?
Options:
a. $1.05
b. $1.30
c. $1.60
d. $20.80
Answer:
b. $1.30
Explanation:
Four friends earned $5.20 for washing a car. They shared the money equally.
$5.20/4 = $1.30
Question 2.
Which represents the value of one $1 bill and 5 quarters?
Options:
a. $1.05
b. $1.25
c. $1.50
d. $2.25
Answer:
d. $2.25
Explanation:
one $1 bill and 5 quarters. 5 quarters = 5 x 0.25 = 1.25.
$1 + $1.25 = $2.25
Spiral Review
Question 3.
Bethany has 9 pennies. What fraction of a dollar is this?
Options:
a. \(\frac{9}{100}\)
b. \(\frac{9}{10}\)
c. \(\frac{90}{100}\)
d. \(\frac{99}{100}\)
Answer:
a. \(\frac{9}{100}\)
Explanation:
1 dollar = 100 pennies.
So, 9 pennies = 9/100 of a dollar
Question 4.
Michael made \(\frac{9}{12}\) of his free throws at practice. What is \(\frac{9}{12}\) in simplest form?
Options:
a. \(\frac{1}{4}\)
b. \(\frac{3}{9}\)
c. \(\frac{1}{2}\)
d. \(\frac{3}{4}\)
Answer:
d. \(\frac{3}{4}\)
Explanation:
\(\frac{9}{12}\) is divided by 3 that is equal to d. \(\frac{3}{4}\).
Question 5.
I am a prime number between 30 and 40. Which number could I be?
Options:
a. 31
b. 33
c. 36
d. 39
Answer:
a. 31
Explanation:
31 has fractions 1 and 31.
Question 6.
Georgette is using the benchmark \(\frac{1}{2}\) to compare fractions. Which statement is correct?
Options:
a. \(\frac{3}{8}>\frac{1}{2}\)
b. \(\frac{2}{5}<\frac{1}{2}\)
c. \(\frac{7}{12}<\frac{1}{2}\)
d. \(\frac{9}{10}=\frac{1}{2}\)
Answer:
b. \(\frac{2}{5}<\frac{1}{2}\)
Explanation:
From the given details, \(\frac{2}{5}<\frac{1}{2}\) is the correct answer.
Page No. 525
Choose the best term from the box to complete the sentence.
Question 1.
A symbol used to separate the ones and the tenths place is called a __________.
__________
Answer:
decimal point
Question 2.
The number 0.4 is written as a ____________.
__________
Answer:
4 tenths or 40 hundredths
Question 3.
A ______________ is one of one hundred equal parts of a whole.
__________
Answer:
hundredth
Write the fraction or mixed number and the decimal shown by the model.
Question 4.
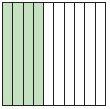
Type below:
________
Answer:
\(\frac{4}{10}\) = 0.4
Explanation:
From the given model, 4 boxes are shaded out of 10 boxes. So, the fraction is \(\frac{4}{10}\) = 0.4
Question 5.
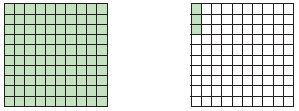
Type below:
________
Answer:
1\(\frac{3}{100}\) = 1.03
Explanation:
The model is divided into 100 equal parts. Each part represents the one-hundredth.
1\(\frac{3}{100}\) is 1 whole and 3 hundredths.
Write the number as hundredths in fraction form and decimal form.
Question 6.
\(\frac{8}{10}\)
Type below:
________
Answer:
\(\frac{80}{100}\)

0.80
Explanation:
Write \(\frac{8}{10}\) as an equivalent fraction.
\(\frac{8}{10}\) =\(\frac{8 × 10}{10× 10}\) = \(\frac{80}{100}\)
8 tenths is the same as 8 tenths 0 hundredths. So the decimal form = 0.80
Question 7.
0.5
Type below:
________
Answer:
\(\frac{50}{100}\)

0.50
Explanation:
Write 0.5 = \(\frac{5}{10}\) as an equivalent fraction.
\(\frac{5}{10}\) =\(\frac{5 × 10}{10× 10}\) = \(\frac{50}{100}\)
5 tenths is the same as 5 tenths 0 hundredths and also 0.50
Question 8.
Type below:
________
Answer:
b. \(\frac{2}{5}<\frac{1}{2}\)
Explanation:
Write the fraction or mixed number as a money amount, and as a decimal in terms of dollars.
Question 9.
\(\frac{95}{100}\)
amount: $ _____ decimal: _____ of a dollar
Answer:
amount: $0.95; decimal: 0.95
Explanation:
Write down 95 with the decimal point 2 spaces from the right (because 100 has 2 zeros)
Question 10.
1 \(\frac{48}{100}\)
amount: $ _____ decimal: _____ of a dollar
Answer:
amount: $1.48; decimal: 1.48
Explanation:
1\(\frac{48}{100}\) = \(\frac{148}{100}\)
Write down 148 with the decimal point 2 spaces from the right (because 100 has 2 zeros). So, 1.48 is the answer
Question 11.
\(\frac{4}{100}\)
amount: $ _____ decimal: _____ of a dollar
Answer:
amount: $0.04; decimal: 0.04
Explanation:
Write down 4 with the decimal point 2 spaces from the right (because 100 has 2 zeros). So, the answer is 0.04
Page No. 526
Question 12.
Ken’s turtle competed in a 0.50-meter race. His turtle had traveled \(\frac{4}{100}\)
meter when the winning turtle crossed the finish line. What is \(\frac{4}{100}\) written as a decimal?
_____
Answer:
decimal: 0.04
Explanation:
Write down 4 with the decimal point 2 spaces from the right (because 100 has 2 zeros). So, the answer is 0.04
Question 13.
Alex lives eight tenths of a mile from Sarah. What is eight tenths written as a decimal?
_____
Answer:
decimal: 0.8
Explanation:
Write down 8 with the decimal point 1 space from the right (because 100 has 1 zero). The decimal value of eight tenths is 0.8
Question 14.
What fraction and decimal, in hundredths, is equivalent to \(\frac{7}{10}\)?
Type below:
________
Answer:
\(\frac{7 x 10}{10 x 10}\) = 0.70
Explanation:
\(\frac{7}{10}\) = \(\frac{7 x 10}{10 x 10}\) = 0.70
Question 15.
Elaine found the following in her pocket. How much money was in her pocket?

$ _____
Answer:
$\(\frac{140}{100}\)
Explanation:
Given that 1 dollar, 1 quarter, 1 dime, 1 Nickel.
1 + 25/100 + 10/100 + 5/100 = 1 + 40/100 = 140/100
Question 16.
Three girls share $0.60. Each girl gets the same amount. How much money does each girl get?
$ _____
Answer:
$0.20
Explanation:
Three girls share $0.60. Each girl gets the same amount. So, $0.60/3 = $0.20
Question 17.
The deli scale weighs meat and cheese in hundredths of a pound. Sam put \(\frac{5}{10}\) pound of pepperoni on the deli scale. What weight does the deli scale show?
_____ hundredths
Answer:
50 hundredths
Explanation:
\(\frac{5}{10}\) = \(\frac{5 x 10}{10 x 10}\) = \(\frac{50}{100}\).
\(\frac{50}{100}\) written as 50 hundredths.
Page No. 529
Question 1.
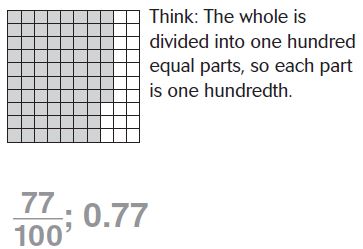
Find \(\frac{7}{10}+\frac{5}{100}\)
Think: Write the addends as fractions with a common denominator.
\(\frac{■}{100}\) + \(\frac{■}{100}\) = \(\frac{■}{■}\)
\(\frac{□}{□}\)
Answer:
\(\frac{75}{100}\)
Explanation:
\(\frac{7}{10}+\frac{5}{100}\).
Write the addends as fractions with a common denominator
\(\frac{7}{10}\) = \(\frac{7 X 10}{10 X 10}\) = \(\frac{70}{100}\).
\(\frac{70}{100}+\frac{5}{100}\) = \(\frac{75}{100}\)
Find the sum.
Question 2.
\(\frac{1}{10}+\frac{11}{100}\) = \(\frac{□}{□}\)
Answer:
\(\frac{21}{100}\)
Explanation:
\(\frac{1}{10}+\frac{11}{100}\).
Write the addends as fractions with a common denominator
\(\frac{1}{10}\) = \(\frac{1 X 10}{10 X 10}\) = \(\frac{10}{100}\).
\(\frac{10}{100}+\frac{11}{100}\) = \(\frac{21}{100}\)
Question 3.
\(\frac{36}{100}+\frac{5}{10}\) = \(\frac{□}{□}\)
Answer:
\(\frac{86}{100}\)
Explanation:
\(\frac{36}{100}+\frac{5}{10}\).
Write the addends as fractions with a common denominator
\(\frac{5}{10}\) = \(\frac{5 X 10}{10 X 10}\) = \(\frac{50}{100}\).
\(\frac{36}{100}+\frac{50}{100}\) = \(\frac{86}{100}\).
Question 4.
$0.16 + $0.45 = $ _____
Answer:
$0.61
Explanation:
Think 0.16 as 16 hundredths = \(\frac{16}{100}\).
Think 0.45 as 45 hundredths = \(\frac{45}{100}\).
Write the addends as fractions with a common denominator
\(\frac{16}{100}\) + \(\frac{45}{100}\) = \(\frac{61}{100}\) = 0.61
Question 5.
$0.08 + $0.88 = $ _____
Answer:
$0.96
Explanation:
Think 0.08 as 8 hundredths = \(\frac{8}{100}\).
Think 0.88 as 88 hundredths = \(\frac{88}{100}\).
Write the addends as fractions with a common denominator.
\(\frac{8}{100}\) + \(\frac{88}{100}\) = \(\frac{96}{100}\) = 0.96
Question 6.
\(\frac{6}{10}+\frac{25}{100}\) = \(\frac{□}{□}\)
Answer:
\(\frac{85}{100}[/latex
Explanation:
[latex]\frac{6}{10}+\frac{25}{100}\)
Write the addends as fractions with a common denominator.
\(\frac{6}{10}\) = \(\frac{6 X 10}{10 X 10}\) = \(\frac{60}{100}\).
\(\frac{60}{100}+\frac{25}{100}\) = \(\frac{85}{100}\).
Question 7.
\(\frac{7}{10}+\frac{7}{100}\) = \(\frac{□}{□}\)
Answer:
50 hundredths
Explanation:
\(\frac{7}{10}+\frac{7}{100}\)
Write the addends as fractions with a common denominator.
\(\frac{7}{10}\) = \(\frac{7 X 10}{10 X 10}\) = \(\frac{70}{100}\).
\(\frac{70}{100}+\frac{7}{100}\) = \(\frac{77}{100}\).
Question 8.
$0.55 + $0.23 = $ _____
Answer:
$0.78
Explanation:
Think 0.55 as 55 hundredths = \(\frac{55}{100}\).
Think 0.23 as 23 hundredths = \(\frac{23}{100}\).
Write the addends as fractions with a common denominator.
\(\frac{55}{100}\) + \(\frac{23}{100}\) = \(\frac{78}{100}\) = 0.78.
Question 9.
$0.19 + $0.13 = $ _____
Answer:
$0.32
Explanation:
Think 0.19 as 19 hundredths = \(\frac{19}{100}\).
Think 0.13 as 13 hundredths = \(\frac{13}{100}\).
Write the addends as fractions with a common denominator.
\(\frac{19}{100}\) + \(\frac{13}{100}\) = \(\frac{32}{100}\) = 0.32.
Reason Quantitatively Algebra Write the number that makes the equation true.
Question 10.
\(\frac{20}{100}+\frac{■}{10}\) = \(\frac{60}{100}\)
■ = _____
Answer:
■ = 4
Explanation:
\(\frac{20}{100}+\frac{■}{10}\) = \(\frac{60}{100}\).
Let the unknown number = s.
If s = 4,
\(\frac{20}{100}+\frac{4}{10}\).
Write the addends as fractions with a common denominator.
\(\frac{4}{10}\) = \(\frac{4 X 10}{10 X 10}\) = \(\frac{40}{100}\).
\(\frac{20}{100}+\frac{40}{100}\) = \(\frac{60}{100}\).
So, the unknown number is 4.
Question 11.
\(\frac{2}{10}+\frac{■}{100}\) = \(\frac{90}{100}\)
■ = _____
Answer:
■ = 70
Explanation:
\(\frac{2}{10}+\frac{■}{100}\) = \(\frac{90}{100}\).
Let the unknown number = s.
If s = 70,
\(\frac{2}{10}+\frac{7}{100}\).
Write the addends as fractions with a common denominator.
\(\frac{2}{10}\) = \(\frac{2 X 10}{10 X 10}\) = \(\frac{20}{100}\).
\(\frac{20}{100}+\frac{70}{100}\) = \(\frac{90}{100}\).
So, the unknown number is 70.
Question 12.
Jerry had 1 gallon of ice cream. He used \(\frac{3}{10}\) gallon to make chocolate milkshakes and 0.40 gallon to make vanilla milkshakes. How much ice cream does Jerry have left after making the milkshakes?
_____ gallon
Answer:
0.30 gallon
Explanation:
Jerry had 1 gallon of ice cream. He used \(\frac{3}{10}\) gallon to make chocolate milkshakes and 0.40 gallon to make vanilla milkshakes.
So, write 0.40 as \(\frac{40}{100}\) gallon.
She used \(\frac{3}{10}\) + \(\frac{40}{100}\).
\(\frac{3}{10}\) = \(\frac{3 X 10}{10 X 10}\) = \(\frac{30}{100}\).
\(\frac{30}{100}\) + \(\frac{40}{100}\) = \(\frac{70}{100}\)
Jerry have left 1 – \(\frac{70}{100}\) = \(\frac{30}{100}\) = 0.30 gallon
Page No. 530
Use the table for 13−16.
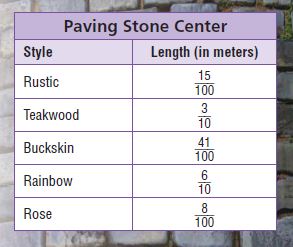
Question 13.
Dean selects Teakwood stones and Buckskin stones to pave a path in front of his house. How many meters long will each set of one Teakwood stone and one Buckskin stone be?
_____ meter
Answer:
\(\frac{71}{100}\) meter
Explanation:
Dean selects Teakwood stones and Buckskin stones to pave a path in front of his house.
Teakwood stone and one Buckskin stone = \(\frac{3}{10}\) + \(\frac{41}{100}\).
Write the addends as fractions with a common denominator.
\(\frac{3}{10}\) = \(\frac{3 X 10}{10 X 10}\) = \(\frac{30}{100}\).
\(\frac{30}{100}\) + \(\frac{41}{100}\) = \(\frac{71}{100}\)
Question 14.
The backyard patio at Nona’s house is made from a repeating pattern of one Rose stone and one Rainbow stone. How many meters long is each pair of stones?
_____ meter
Answer:
\(\frac{68}{100}\) meter
Explanation:
The backyard patio at Nona’s house is made from a repeating pattern of one Rose stone and one Rainbow stone.
Each pair of stone = \(\frac{8}{100}\) + \(\frac{6}{10}\).
\(\frac{6}{10}\) = \(\frac{6 X 10}{10 X 10}\) = \(\frac{60}{100}\).
Each pair of stone = \(\frac{8}{100}\) + \(\frac{60}{100}\) = \(\frac{68}{100}\).
Question 15.
For a stone path, Emily likes the look of a Rustic stone, then a Rainbow stone, and then another Rustic stone. How long will the three stones in a row be? Explain.
_____ meter
Answer:
\(\frac{90}{100}\) meter
Explanation:
For a stone path, Emily likes the look of a Rustic stone, then a Rainbow stone, and then another Rustic stone. If three stones in a row, then
\(\frac{15}{100}\) + \(\frac{6}{10}\) + \(\frac{15}{100}\).
\(\frac{30}{100}\) + \(\frac{6}{10}\).
\(\frac{6}{10}\) = \(\frac{6 X 10}{10 X 10}\) = \(\frac{60}{100}\).
\(\frac{30}{100}\) + \(\frac{60}{100}\) = \(\frac{90}{100}\).
Question 16.
Which two stones can you place end-to-end to get a length of 0.38 meter? Explain how you found your answer.
Type below:
________
Answer:
If you add Teakwood stones and Rose stones, then you get a length of 0.38 meter.
\(\frac{3}{10}\) + \(\frac{8}{100}\).
\(\frac{3}{10}\) = \(\frac{3 X 10}{10 X 10}\) = \(\frac{30}{100}\).
\(\frac{30}{100}\) + \(\frac{8}{100}\) = latex]\frac{38}{100}[/latex] = 0.38.
If you add any other two stones, the answer will not equal to 0.38.
Question 17.
Christelle is making a dollhouse. The dollhouse is \(\frac{6}{10}\) meter tall without the roof. The roof is \(\frac{15}{100}\) meter high. What is the height of the dollhouse with the roof? Choose a number from each column to complete an equation to solve.

\(\frac{□}{□}\) meter
Answer:
\(\frac{60}{100}\) + \(\frac{15}{100}\) = \(\frac{75}{100}\) meter
Explanation:
\(\frac{6}{10}\) + \(\frac{15}{100}\).
\(\frac{6}{10}\) = \(\frac{6 X 10}{10 X 10}\) = \(\frac{60}{100}\).
\(\frac{60}{100}\) + \(\frac{15}{100}\) = \(\frac{75}{100}\).
Common Core – New – Page No. 531
Add Fractional Parts of 10 and 100
Find the sum.
Question 1.
\(\frac{2}{10}+\frac{43}{100}\) Think: Write \(\frac{2}{10}\) as a fraction with a denominator of 100: \(\frac{2 \times 10}{10 \times 10}=\frac{20}{100}\)
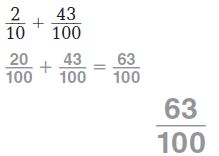
Answer:
\(\frac{63}{100}\)
Explanation:
Think: Write \(\frac{2}{10}\) as a fraction with a denominator of 100: \(\frac{2 \times 10}{10 \times 10}=\frac{20}{100}\)
Question 2.
\(\frac{17}{100}+\frac{6}{10}\)
\(\frac{□}{□}\)
Answer:
\(\frac{77}{100}\)
Explanation:
\(\frac{17}{100}+\frac{6}{10}\).
\(\frac{6 \times 10}{10 \times 10}=\frac{60}{100}\)
\(\frac{17}{100}+\frac{60}{100}\) = \(\frac{77}{100}\)
Question 3.
\(\frac{9}{100}+\frac{4}{10}\)
\(\frac{□}{□}\)
Answer:
\(\frac{49}{100}\)
Explanation:
\(\frac{9}{100}+\frac{4}{10}\).
\(\frac{4 \times 10}{10 \times 10}=\frac{40}{100}\)
\(\frac{9}{100}+\frac{40}{100}\) = \(\frac{49}{100}\)
Question 4.
\(\frac{7}{10}+\frac{23}{100}\)
\(\frac{□}{□}\)
Answer:
\(\frac{93}{100}\)
Explanation:
\(\frac{7}{10}+\frac{23}{100}\).
\(\frac{7 \times 10}{10 \times 10}=\frac{70}{100}\)
\(\frac{70}{100}+\frac{23}{100}\) = \(\frac{93}{100}\)
Question 5.
$0.48 + $0.30
$ _____
Answer:
$0.78
Explanation:
Think $0.48 as \(\frac{48}{100}\).
Think $0.30 as \(\frac{30}{100}\).
\(\frac{48}{100}+\frac{30}{100}\) = \(\frac{78}{100}\) = $0.78
Question 6.
$0.25 + $0.34
$ _____
Answer:
$0.59
Explanation:
Think $0.25 as \(\frac{25}{100}\).
Think $0.34 as \(\frac{34}{100}\).
\(\frac{25}{100}+\frac{34}{100}\) = \(\frac{59}{100}\) = $0.59
Question 7.
$0.66 + $0.06
$ _____
Answer:
$0.72
Explanation:
Think $0.66 as \(\frac{66}{100}\).
Think $0.06 as \(\frac{6}{100}\).
\(\frac{66}{100}+\frac{6}{100}\) = \(\frac{72}{100}\) = $0.72
Problem Solving
Question 8.
Ned’s frog jumped \(\frac{38}{100}\) meter. Then his frog jumped \(\frac{4}{10}\) meter. How far did Ned’s frog jump in all?
\(\frac{□}{□}\)
Answer:
\(\frac{78}{100}\) meter
Explanation:
Ned’s frog jumped \(\frac{38}{100}\) meter. Then his frog jumped \(\frac{4}{10}\) meter.
So, together \(\frac{38}{100}\) + \(\frac{4}{10}\) jumped.
\(\frac{4}{10}\) = \(\frac{4 \times 10}{10 \times 10}=\frac{40}{100}\).
\(\frac{38}{100}\) + \(\frac{40}{100}\) = \(\frac{78}{100}\).
Question 9.
Keiko walks \(\frac{5}{10}\) kilometer from school to the park. Then she walks \(\frac{19}{100}\) kilometer from the park to her home. How far does Keiko walk in all?
\(\frac{□}{□}\)
Answer:
\(\frac{69}{100}\) kilometer
Explanation:
Keiko walks \(\frac{5}{10}\) kilometer from school to the park. Then she walks \(\frac{19}{100}\) kilometer from the park to her home.
Total = \(\frac{5}{10}\) + \(\frac{19}{100}\) kilometer.
\(\frac{5}{10}\) = \(\frac{5 \times 10}{10 \times 10}=\frac{50}{100}\).
\(\frac{50}{100}\) + \(\frac{19}{100}\) = \(\frac{69}{100}\).
Common Core – New – Page No. 532
Lesson Check
Question 1.
In a fish tank, \(\frac{2}{10}\) of the fish were orange and \(\frac{5}{100}\) of the fish were striped. What fraction of the fish were orange or striped?
Options:
a. \(\frac{7}{10}\)
b. \(\frac{52}{100}\)
c. \(\frac{25}{100}\)
d. \(\frac{7}{100}\)
Answer:
c. \(\frac{25}{100}\)
Explanation:
In a fish tank, \(\frac{2}{10}\) of the fish were orange and \(\frac{5}{100}\) of the fish were striped.
To find the raction of the fish were orange or striped Add \(\frac{2}{10}\) and \(\frac{5}{100}\).
\(\frac{2}{10}\) = \(\frac{2 \times 10}{10 \times 10}=\frac{20}{100}\).
\(\frac{20}{100}\) + \(\frac{5}{100}\) = \(\frac{25}{100}\).
Question 2.
Greg spends $0.45 on an eraser and $0.30 on a pen. How much money does Greg spend in all?
Options:
a. $3.45
b. $0.75
c. $0.48
d. $0.15
Answer:
b. $0.75
Explanation:
Think $0.45 as \(\frac{45}{100}\).
Think $0.30 as \(\frac{30}{100}\).
\(\frac{45}{100}+\frac{30}{100}\) = \(\frac{75}{100}\) = $0.75.
Spiral Review
Question 3.
Phillip saves $8 each month. How many months will it take him to save at least $60?
Options:
a. 6 months
b. 7 months
c. 8 months
d. 9 months
Answer:
c. 8 months
Explanation:
Phillip saves $8 each month.
To save at least $60, \(\frac{60}{8}\) = 8 months (approximately)
Question 4.
Ursula and Yi share a submarine sandwich. Ursula eats \(\frac{2}{8}\) of the sandwich. Yi eats \(\frac{3}{8}\) of the sandwich. How much of the sandwich do the two friends eat?
Options:
a. \(\frac{1}{8}\)
b. \(\frac{4}{8}\)
c. \(\frac{5}{8}\)
d. \(\frac{6}{8}\)
Answer:
c. \(\frac{5}{8}\)
Explanation:
Ursula and Yi share a submarine sandwich. Ursula eats \(\frac{2}{8}\) of the sandwich. Yi eats \(\frac{3}{8}\) of the sandwich.
Two friends eat \(\frac{2}{8}\) + \(\frac{3}{8}\) = \(\frac{5}{8}\)
Question 5.
A carpenter has a board that is 8 feet long. He cuts off two pieces. One piece is 3 \(\frac{1}{2}\) feet long and the other is 2 \(\frac{1}{3}\) feet long. How much of the board is left?
Options:
a. 2 \(\frac{1}{6}\)
b. 2 \(\frac{5}{6}\)
c. 3 \(\frac{1}{6}\)
d. 3 \(\frac{5}{6}\)
Answer:
a. 2 \(\frac{1}{6}\)
Explanation:
3 \(\frac{1}{2}\) = \(\frac{7}{2}\).
2 \(\frac{1}{3}\) = \(\frac{7}{3}\).
A carpenter has a board that is 8 feet long. He cuts off two pieces. One piece is 3 \(\frac{1}{2}\) feet long and the other is 2 \(\frac{1}{3}\) feet long.
\(\frac{7}{2}\) + \(\frac{7}{3}\) = \(\frac{7 \times 3}{2\times 3} + [latex]\frac{7 \times 2}{3\times 2} = [latex]\frac{21}{6}\) + \(\frac{14}{6}\) = \(\frac{35}{6}\) = 5\(\frac{5}{6}\).
He left 8 – 5\(\frac{5}{6}\).
7\(\frac{6}{6}\) – 5\(\frac{5}{6}\) = 2\(\frac{1}{6}\)
Question 6.
Jeff drinks \(\frac{2}{3}\) of a glass of juice. Which fraction is equivalent to \(\frac{2}{3}\)?
Options:
a. \(\frac{1}{3}\)
b. \(\frac{3}{2}\)
c. \(\frac{3}{6}\)
d. \(\frac{8}{12}\)
Answer:
d. \(\frac{8}{12}\)
Explanation:
\(\frac{8}{12}\) is divided by 4. So, \(\frac{8}{12}\) = \(\frac{2}{3}\).
Page No. 535
Question 1.
Compare 0.39 and 0.42. Write <, >, or =.
Shade the model to help.
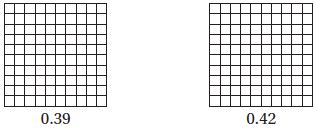
0.39 ____ 0.42
Answer:
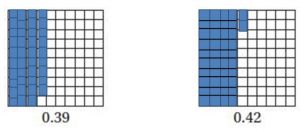
0.39 < 0.42
Compare. Write <, >, or =.
Question 2.
0.26 ____ 0.23
Answer:
0.26 > 0.23
Explanation:
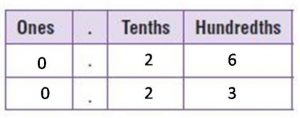
The digits in the one’s and tenths place are the same. Compare the digits in the hundredths place. 6 > 3. So, 0.26 > 0.23.
Question 3.
0.7 ____ 0.54
Answer:
0.7 > 0.54
Explanation:
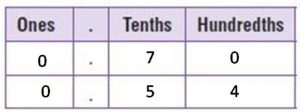
The digits in the ones place are the same. Compare the digits in the tenths place. 0.7 = 0.70. 7 > 5. So, 0.70 > 0.54.
Question 4.
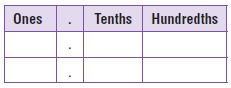
1.15 ____ 1.3
Answer:
1.15 < 1.3
Explanation:
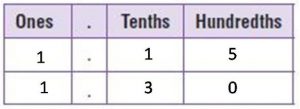
The digits in the ones place are the same. Compare the digits in the tenths place. 1 < 3. So, 1.15 < 1.3
Question 5.
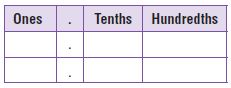
4.5 ____ 2.89
Answer:
4.5 > 2.89
Explanation:
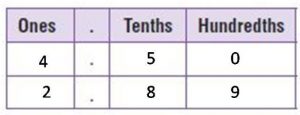
Compare one’s digits. 4 > 2 . So, 4.5 > 2.89
Compare. Write <, >, or =.
Question 6.
0.9 ____ 0.81
Answer:
0.9 > 0.81
Explanation:
0.9 is 9 tenths, which is equivalent to 90 hundredths.
0.81 is 81 hundredths.
90 hundredths > 81 hundredths. So, 0.9 > 0.81.
Question 7.
1.06 ____ 0.6
Answer:
1.06 > 0.6
Explanation:
1.06 is 106 hundredths.
0.6 is 6 tenths, which is equivalent to 60 hundredths.
106 hundredths > 60 hundredths. So, 1.06 > 0.6.
Question 8.
0.25 ____ 0.3
Answer:
0.25 < 0.3
Explanation:
0.25 is 25 hundredths.
0.3 is 3 tenths, which is equivalent to 30 hundredths.
25 hundredths < 30 hundredths. So, 0.25 < 0.3.
Question 9.
2.61 ____ 3.29
Answer:
2.61 < 3.29
Explanation:
2.61 is 261 hundredths.
3.29 is 329 hundredths.
261 hundredths < 329 hundredths. So, 2.61 < 3.29.
Reason Quantitatively Compare. Write <, >, or =.
Question 10.
0.30 ____ \(\frac{3}{10}\)
Answer:
0.30 = \(\frac{3}{10}\)
Explanation:
0.30 is 30 hundredths.
\(\frac{3}{10}\) is 3 tenths, which is equal to 30 hundredths.
30 hundredths = 30 hundredths. So, 0.30 = \(\frac{3}{10}\).
Question 11.
\(\frac{4}{100}\) ____ 0.2
Answer:
\(\frac{4}{100}\) < 0.2
Explanation:
\(\frac{4}{100}\) is 4 hundredths.
0.2 is 2 tenths, which is equal to 20 hundredths.
4 hundredths < 20 hundredths. So, \(\frac{4}{100}\) < 0.2
Question 12.
0.15 ____ \(\frac{1}{10}\)
Answer:
0.15 > \(\frac{1}{10}\)
Explanation:
0.15 is 15 hundredths.
\(\frac{1}{10}\) is 1 tenths, which is equal to 10 hundredths.
15 hundredths > 10 hundredths. So, 0.15 > \(\frac{1}{10}\).
Question 13.
\(\frac{1}{8}\) ____ 0.8
Answer:
latex]\frac{1}{8}[/latex] < 0.8
Explanation:
\(\frac{1}{8}\) = 0.25 is 25 hundredths.
0.8 is 8 tenths, which is equal to 80 hundredths.
25 hundredths < 80 hundredths. So, \(\frac{1}{8}\) < 0.8
Question 14.
Robert had $14.53 in his pocket. Ivan had $14.25 in his pocket. Matt had $14.40 in his pocket. Who had more money, Robert or Matt? Did Ivan have more money than either Robert or Matt?
________
Answer:
Robert had more money.
No, Ivan didn’t have more money than either Robert or Matt.
Explanation:
Compare Robert, Ivan, and Matt money to know who had more money.
The digits in the one’s place are the same. Compare the digits in the tenths place. 5 > 4 > 2. So, Robert had more money.
Page No. 536
Question 15.
Ricardo and Brandon ran a 1500-meter race. Ricardo finished in 4.89 minutes. Brandon finished in 4.83 minutes. What was the time of the runner who finished first?
a. What are you asked to find?–
Type below:
________
Answer:
The time of the runner who finished first.
Question 15.
b. What do you need to do to find the answer?
Type below:
________
Answer:
I have to compare the times to find the time that is less.
Question 15.
c. Solve the problem.
Type below:
________
Answer:
Use place-value chart
The digits of the one’s and tenths are equal. So, compare hundredths to find greater time.
9 > 3.
4.83 minutes are less than 4.89.
Question 15.
d. What was the time of the runner who finished first?
______ minutes
Answer:
4.83 minutes
Question 15.
e. Look back. Does your answer make sense? Explain.
_____
Answer:
Yes. The time of the runner who finished first is the lesser time of the two. Since 4.83, 4.89, then 4.83 minutes is the time of the runner who finished first.
Question 16.
The Venus flytrap closes in 0.3 second and the waterwheel plant closes in 0.2 second. What decimal is halfway between 0.2 and 0.3? Explain.
_____
Answer:
0.2 is 2 tenths, which is equal to the 20 hundredths.
0.3 is 3 tenths, which is equal to 30 hundredths.
The halfway between 20 hundredths and 30 hundredths is 25 hundredths.
So, the answer is 0.25.
Question 17.
For numbers 17a–17c, select True or False for the inequality.
a. 0.5 > 0.53
i. True
ii. False
Answer:
ii. False
Explanation:
0.5 is 50 hundredths.
0.53 is 53 hundredths.
50 hundredths < 53 hundredths. So, 0.5 < 0.53. So, the answer is false.
Question 17.
b. 0.35 < 0.37
i. True
ii. False
Answer:
i. True
Explanation:
0.35 is 35 hundredths.
0.37 is 37 hundredths.
35 hundredths < 37 hundredths.
0.35 < 0.37.
So, the answer is true.
Question 17. c. $1.35 > $0.35
i. True
ii. False
Answer:
i. True
Explanation:
$1.35 is 135 hundredths.
$0.35 is 35 hundredths.
135 hundredths > 35 hundredths.
$1.35 > $0.35.
So, the answer is correct.
Common Core – New – Page No. 537
Compare Decimals
Compare. Write <. >, or =.
Question 1.

Think: 3 tenths is less than 5 tenths. So, 0.35 < 0.53
Answer:
0.35 < 0.53
Explanation:
3 tenths is less than 5 tenths. So, 0.35 < 0.53
Question 2.
0.6 ______ 0.60
Answer:
0.6 = 0.60
Explanation:
0.6 is 6 tenths can write as 6 tenths and 0 hundredths. So, 0.6 = 0.60.
Question 3.
0.24 ______ 0.31
Answer:
0.24 < 0.31
Explanation:
2 tenths is less than 3 tenths. So, 0.24 < 0.31.
Question 4.
0.94 ______ 0.9
Answer:
0.94 > 0.9
Explanation:
The digits of tenths are equal. So, compare hundredths. 4 hundredths is greater than 0 hundredths. So, 0.94 > 0.9.
Question 5.
0.3 ______ 0.32
Answer:
0.3 < 0.32
Explanation:
The digits of tenths are equal. So, compare hundredths. 0 hundredths is less than 2 hundredths. So, 0.3 < 0.32.
Question 6.
0.45 ______ 0.28
Answer:
0.45 > 0.28
Explanation:
4 tenths is greater than 2 tenths. So, 0.45 > 0.28.
Question 7.
0.39 ______ 0.93
Answer:
0.39 < 0.93
Explanation:
3 tenths is less than 9 tenths. So, 0.39 < 0.93.
Use the number line to compare. Write true or false.

Question 8.
0.8 > 0.78
______
Answer:
true
Explanation:
0.78 is in between 0.7 and 0.8 that is less than 0.8. So, 0.8 > 0.78.
Question 9.
0.4 > 0.84
______
Answer:
false
Explanation:
0.4 is less than 0.84 and the left side of the number line. So, 0.4 < 0.84. The answer is false.
Question 10.
0.7 > 0.70
______
Answer:
false
Explanation:
0.7 is 7 tenths and 70 hundredths. 0.7 = 0.70. So, the answer is false.
Question 11.
0.4 > 0.04
______
Answer:
true
Explanation:
0.04 is less than 0.4 and it is left side of the 0.1 on the number line. 0.1 is less than 0.4. So, the given answer is true.
Compare. Write true or false.
Question 12.
0.09 > 0.1
______
Answer:
false
Explanation:
0 tenths is less than 1 tenths. So, 0.09 < 0.1. So, the answer is false.
Question 13.
0.24 = 0.42
______
Answer:
false
Explanation:
2 tenths is less than 4 tenths. So, 0.24 < 0.42. So, the answer is false.
Question 14.
0.17 < 0.32 ______
Answer:
true
Explanation:
1 tenths is less than 3 tenths. So, 0.17 < 0.32. So, the answer is true.
Question 15.
0.85 > 0.82
______
Answer:
true
Explanation:
The digits of tenths are equal. So, compare hundredths. 5 hundredths is greater than 2 hundredths. So, 0.85 > 0.82.
Question 16.
Kelly walks 0.7 mile to school. Mary walks 0.49 mile to school. Write an inequality using <, > or = to compare the distances they walk to school.
0.7 ______ 0.49
Answer:
0.7 > 0.49
Explanation:
7 tenths is greater than 4 tenths. So, 0.7 > 0.49.
Question 17.
Tyrone shades two decimal grids. He shades 0.03 of the squares on one grid blue. He shades 0.3 of another grid red. Which grid has the greater part shaded?
0.03 ______ 0.3
Answer:
0.03 < 0.3
Explanation:
0.03 is 3 hundredths.
0.3 is 3 tenths, which is equal to 30 hundredths.
3 hundredths < 30 hundredths. So, 0.03 < 0.3.
Common Core – New – Page No. 538
Lesson Check
Question 1.
Bob, Cal, and Pete each made a stack of baseball cards. Bob’s stack was 0.2 meter high. Cal’s stack was 0.24 meter high. Pete’s stack was 0.18 meter high.
Which statement is true?
Options:
a. 0.02 > 0.24
b. 0.24 > 0.18
c. 0.18 > 0.2
d. 0.24 = 0.2
Answer:
b. 0.24 > 0.18
Explanation:
2 tenths is greater than 1 tenth. So, 0.24 > 0.18.
Question 2.
Three classmates spent money at the school supplies store. Mark spent 0.5 dollar, Andre spent 0.45 dollar, and Raquel spent 0.52 dollar. Which
statement is true?
Options:
a. 0.45 > 0.5
b. 0.52 < 0.45
c. 0.5 = 0.52
d. 0.45 < 0.5
Answer:
d. 0.45 < 0.5
Explanation:
4 tenths is less than 5 tenth. So, 0.45 > 0.5.
Spiral Review
Question 3.
Pedro has $0.35 in his pocket. Alice has $0.40 in her pocket. How much money do Pedro and Alice have in their pockets altogether?
Options:
a. $0.05
b. $0.39
c. $0.75
d. $0.79
Answer:
c. $0.75
Explanation:
Pedro has $0.35 in his pocket. Alice has $0.40 in her pocket.
Together = $0.35 + $0.40 = $0.75.
Question 4.
The measure 62 centimeters is equivalent to \(\frac{62}{100}\) meter. What is this measure written as a decimal?
Options:
a. 62.0 meters
b. 6.2 meters
c. 0.62 meter
d. 0.6 meter
Answer:
c. 0.62 meter
Explanation:
\(\frac{62}{100}\) = 0.62 meter.
Question 5.
Joel has 24 sports trophies. Of the trophies, \(\frac{1}{8}\) are soccer trophies. How many soccer trophies does Joel have?
Options:
a. 2
b. 3
c. 4
d. 6
Answer:
b. 3
Explanation:
Joel has 24 sports trophies. Of the trophies, \(\frac{1}{8}\) are soccer trophies.
So, \(\frac{1}{8}\) X 24 = 3 soccer trophies.
Question 6.
Molly’s jump rope is 6 \(\frac{1}{3}\) feet long. Gail’s jump rope is 4 \(\frac{2}{3}\) feet long. How much longer is Molly’s jump rope?
Options:
a. 1 \(\frac{1}{3}\) feet
b. 1 \(\frac{2}{3}\) feet
c. 2 \(\frac{1}{3}\) feet
d. 2 \(\frac{2}{3}\) feet
Answer:
b. 1 \(\frac{2}{3}\) feet
Explanation:
6 \(\frac{1}{3}\) feet = \(\frac{19}{3}\) feet.
4 \(\frac{2}{3}\) feet = \(\frac{14}{3}\) feet.
\(\frac{19}{3}\) – \(\frac{14}{3}\) = \(\frac{5}{3}\) feet = b. 1 \(\frac{2}{3}\) feet.
Page No. 539
Question 1.
Select a number shown by the model. Mark all that apply.
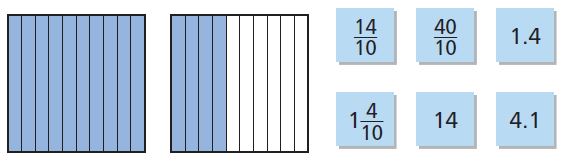
Type below:
________
Answer:
1 \(\frac{4}{10}\) = \(\frac{14}{10}\) = 1.4
Explanation:
from the given image, there is one whole number and \(\frac{4}{10}\) of another model. So, 1 \(\frac{4}{10}\) = \(\frac{14}{10}\) = 1.4
Question 2.
Rick has one dollar and twenty-seven cents to buy a notebook. Which names this money amount in terms of dollars? Mark all that apply.
Options:
a. 12.7
b. 1.027
c. $1.27
d. 1.27
e. 1 \(\frac{27}{100}\)
f. \(\frac{127}{10}\)
Answer:
c. $1.27
d. 1.27
e. 1 \(\frac{27}{100}\)
Explanation:
one dollar and twenty-seven cents = 1 \(\frac{27}{100}\) = 1.27 = $1.27
Question 3.
For numbers 3a–3e, select True or False for the statement.
a. 0.9 is equivalent to 0.90.
i. True
ii. False
Answer:
i. True
Explanation:
0.9 is 9 tenths, which is equal to 90 hundredths. 0.9 = 0.90. So, the answer is true.
Question 3.
b. 0.20 is equivalent to \(\frac{2}{100}\)
i. True
ii. False
Answer:
ii. False
Explanation:
\(\frac{2}{100}\) = 0.02. So, the given answer is false.
Question 3.
c. \(\frac{80}{100}\) is equivalent to \(\frac{8}{10}\).
i. True
ii. False
Answer:
i. True
Explanation:
Divide \(\frac{80}{100}\) by 10 = \(\frac{8}{10}\). So, the answer is true.
Question 3.
d. \(\frac{6}{10}\) is equivalent to 0.60.
i. True
ii. False
Answer:
i. True
Explanation:
\(\frac{6}{10}\) is 0.6. 0.6 is 6 tenths, which is equal to 6 tenths and 0 hundredths. 0.60. So, 0.6 =0.60. The answer is true.
Question 3.
e. 0.3 is equivalent to \(\frac{3}{100}\)
i. True
ii. False
Answer:
ii. False
Explanation:
0.3 is 3 tenths, which is equal to 3 tenths and 0 hundredths. \(\frac{3}{100}\) is 0 tenths. So, the answer is false.
Page No. 540
Question 4.
After selling some old books and toys, Gwen and her brother Max had 5 one-dollar bills, 6 quarters, and 8 dimes. They agreed to divide the money equally.
Part A
Wat is the total amount of money that Gwen and Max earned?
Explain.
$ _____
Answer:
$7.30
Explanation:
After selling some old books and toys, Gwen and her brother Max had 5 one-dollar bills, 6 quarters, and 8 dimes.
5 + (6 X 25/100) + (8 X 10/100) = 5 + 150/100 + 80/100 = 5 + 230/100 = 730/100 = 7.30
Question 4.
Part B
Max said that he and Gwen cannot get equal amounts of money because 5 one-dollar bills cannot be divided evenly. Do you agree with Max?
Explain.
_____
Answer:
ii. False
Explanation:
No; they can share the 3 quarters and 4 dimes each. Then, they can change the 5 dollar bills into quarters. 1 dollar = 4 quarters. So, 5 dollars = 5 X 4 or 20 quarters. They can each get 10 quarters. So, each person has a total of 13 quarters and 4 dimes. $3.25 + $0.40 = $3.65
Question 5.
Harrison rode his bike \(\frac{6}{10}\) of a mile to the park. Shade the model. Then write the decimal to show how far Harrison rode his bike.
![]()
Harrison rode his bike _______ mile to the park.
_____
Answer:
![]()
Harrison rode his bike 0.6 mile to the park.
Explanation:
6 boxes are shaded out of 10.
Question 6.
Amaldo spent \(\frac{88}{100}\) of a dollar on a souvenir pencil from Zion National Park in Utah. What is \(\frac{88}{100}\) written as a decimal in terms of dollars?
_____
Answer:
0.88
Explanation:
Write down 88 with the decimal point 2 spaces from the right (because 100 has 2 zeros). 0.88
Question 7.
Tran has $5.82. He is saving for a video game that costs $8.95.
Tran needs _______ more to have enough money for the game.
_____
Answer:
$3.13
Explanation:
Tran has $5.82. He is saving for a video game that costs $8.95. To know more amount need to buy a video game = $8.95 – $5.82 = $3.13
Page No. 541
Question 8.
Cheyenne lives \(\frac{7}{10}\) mile from school. A fraction in hundredths equal to \(\frac{7}{10}\) is
\(\frac{□}{□}\)
Answer:
\(\frac{70}{100}\)
Explanation:
\(\frac{7}{10}\) = \(\frac{7 \times 10}{10 \times 10}\) = \(\frac{70}{100}\)
Question 9.
Write a decimal in tenths that is less than 2.42 but greater than 2.0.
Type below:
__________
Answer:
2.1, 2.2, 2.3, 2.4
Explanation:
The decimal in greater than 2.0 and below the 2.4 are 2.1, 2.2, 2.3, 2.4
Question 10.
Kylee and two of her friends are at a museum. They find two quarters and one dime on the ground.
Part A
If Kylee and her friends share the money equally, how much will each person get? Explain how you found your answer.
$ _____
Explain:
__________
Answer:
$0.20; Two quarters and one dime are equal to $0.50 + $0.10 = $0.60. Take $0.60 as 6 dimes. When 6 dimes divide equally, each person will receive 2 dimes or $0.20.
Question 10.
Part B
Kylee says that each person will receive \(\frac{2}{10}\) of the money that was found. Do you agree? Explain.
__________
Answer:
No; Each person receives $0.20, which is 2/10 of a dollar, not 2/10 of the money that was found. Since there are 3 people who share the money equally, each person will receive 1/3 of the money.
Question 11.
Shade the model to show 1 \(\frac{52}{100}\). Then write the mixed number in decimal form.
_____
Answer:

1.52
Page No. 542
Question 12.
Henry is making a recipe for biscuits. A recipe calls for \(\frac{5}{10}\) kilogram flour and \(\frac{9}{100}\) kilogram sugar.
Part A
If Henry measures correctly and combines the two amounts, how much flour and sugar will he have? Show your work.
\(\frac{□}{□}\) kilogram
Answer:
\(\frac{59}{100}\) kilogram
Explanation:
Henry is making a recipe for biscuits. A recipe calls for \(\frac{5}{10}\) kilogram flour and \(\frac{9}{100}\) kilogram sugar. So, add \(\frac{5}{10}\) kilogram flour and \(\frac{9}{100}\) kilogram flour.
\(\frac{5}{10}\) = \(\frac{5 \times 10}{10 \times 10}\) = \(\frac{50}{100}\).
\(\frac{50}{100}\) + \(\frac{9}{100}\) = \(\frac{59}{100}\).
Question 12.
Part B
How can you write your answer as a decimal?
__________ kilogram
Answer:
0.59 kilogram
Explanation:
\(\frac{59}{100}\) = 0.59
Question 13.
An orchestra has 100 musicians. \(\frac{4}{10}\) of them play string instruments—violin, viola, cello, double bass, guitar, lute, and harp. What decimal is equivalent to \(\frac{4}{10}\)?
__________
Answer:
0.4 or 0.40
Explanation:
\(\frac{4}{10}\) = 0.4 = 0.40
Question 14.
Complete the table.
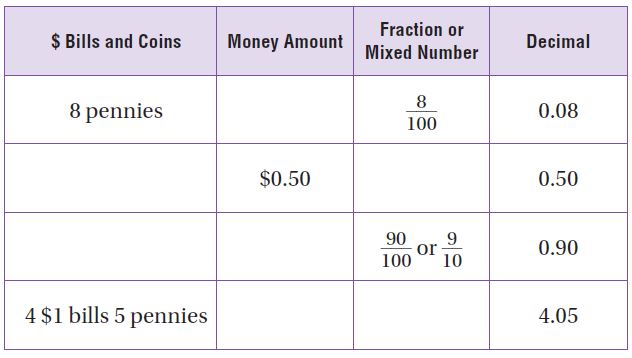
Answer:
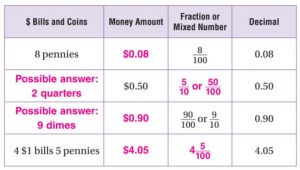
Question 15.
The point on the number line shows the number of seconds it took an athlete to run the forty-yard dash. Write the decimal that correctly names the point.
Answer:
\(\frac{70}{100}\)
Explanation:
The point is in between 5\(\frac{5}{10}\) and 6.0. The point after the 5\(\frac{5}{10}\) is 5\(\frac{6}{10}\) = 5.6
Page No. 543
Question 16.
Ingrid is making a toy car. The toy car is \(\frac{5}{10}\) meter high without the roof. The roof is \(\frac{18}{100}\) meter high. What is the height of the toy car with the roof? Choose a number from each column to complete an equation to solve.
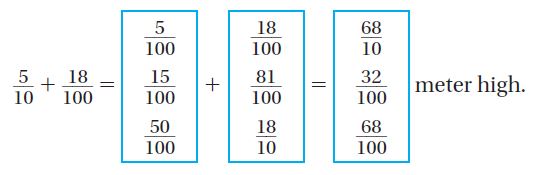
Type below:
__________
Answer:
\(\frac{50}{100}\) + \(\frac{18}{100}\) = \(\frac{68}{100}\) meter high
Explanation:
\(\frac{5}{10}\) = \(\frac{5 \times 10}{10 \times 10}\) = \(\frac{50}{100}\).
\(\frac{50}{100}\) + \(\frac{18}{100}\) = \(\frac{68}{100}\).
Question 17.
Callie shaded the model to represent the questions she answered correctly on a test. What decimal represents the part of the model that is shaded?
represents _____
Answer:
0.81
Explanation:
81 boxes are shaded out of 100. So, \(\frac{81}{100}\) = 0.81
Question 18.
For numbers 18a–18f, select True or False for the inequality.
a. 0.21 < 0.27
i. True
ii. False
Answer:
i. True
Explanation:
The digits in the one’s and tenths place are the same. Compare the digits in the hundredths place. 1 < 7. So, 0.21 < 0.27. The answer is true.
Question 18. b. 0.4 > 0.45
i. True
ii. False
Answer:
ii. False
Explanation:
0.4 = 0.40
The digits in the one’s and tenths place are the same. Compare the digits in the hundredths place. 0 < 5. So, 0.4 < 0.46. The answer is false.
Question 18.
c. $3.21 > $0.2
i. True
ii. False
Answer:
i. True
Explanation:
3 ones is greater than 0’s. So, $3.21 > $0.2
Question 18.
d. 1.9 < 1.90
i. True
ii. False
Answer:
ii. False
Explanation:
1.9 = 1.90. So, the answer is false
Question 18. e. 0.41 = 0.14
i. True
ii. False
Answer:
ii. False
Explanation:
The digits in the one’s are the same. Compare the digits in the tenths place. 4 > 1. So, 0.41 > 0.14. The answer is false.
Question 18. f. 6.2 > 6.02
i. True
ii. False
Answer:
i. True
Explanation:
2 tenths is greater than 0 tenths. So, 6.2 > 6.02. The answer is true.
Question 19.
Fill in the numbers to find the sum.
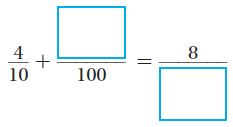
Type below:
__________
Answer:
\(\frac{4}{10}\) + \(\frac{40}{100}\) = \(\frac{8}{10}\)
Explanation:
Let the unknown numbers are A and B.
\(\frac{4}{10}\) + \(\frac{A}{100}\) = \(\frac{8}{B}\)
If A = 40 and B = 10, then \(\frac{4}{10}\) + \(\frac{40}{100}\) = \(\frac{8}{10}\).
Page No. 544
Question 20.
Steve is measuring the growth of a tree. He drew this model to show the tree’s growth in meters. Which fraction, mixed number, or decimal does the model show? Mark all that apply.
Options:
a. 1.28
b. 12.8
c. 0.28
d. 2 \(\frac{8}{100}\)
e. 1 \(\frac{28}{100}\)
f. 1 \(\frac{28}{10}\)
Answer:
a. 1.28
e. 1 \(\frac{28}{100}\)
Explanation:
From the given image, it has one model of 1 whole number and other model is shades 24 boxes out of 100. So, 1 \(\frac{28}{100}\) = \(\frac{128}{100}\) = 1.28 is the answer.
Question 21.
Luke lives 0.4 kilometer from a skating rink. Mark lives 0.25 kilometer from the skating rink.
Part A
Who lives closer to the skating rink? Explain.
_____
Answer:
Mark lives closer to the skating rink
Explanation:
0.4 is 4 tenths and 0.25 is 2 tenths 5 hundredths. Compare the tenths, since
4 tenths > 2 tenths. Luke lives farther from the rink. So, Mark lives closer.
Question 21.
Part B
How can you write each distance as a fraction? Explain.
Type below:
__________
Answer:
\(\frac{4}{10}\) and \(\frac{25}{100}\)
Explanation:
0.4 is 4 tenths. So, \(\frac{4}{10}\) and 0.25 is 25 hundredths. So, \(\frac{25}{100}\).
Question 21.
Part C
Luke is walking to the skating rink to pick up a practice schedule. Then he is walking to Mark’s house. Will he walk more than a kilometer or less than a kilometer? Explain.
__________
Answer:
Less than a kilometer; \(\frac{4}{10}\) < \(\frac{5}{10}\) or \(\frac{1}{2}\) and \(\frac{25}{100}\) < \(\frac{50}{100}\) or \(\frac{1}{2}\).
\(\frac{4}{10}\) + \(\frac{25}{100}\) < \(\frac{1}{2}\) + \(\frac{1}{2}\). So, \(\frac{1}{2}\) + \(\frac{1}{2}\) = 1.
Therefore, \(\frac{4}{10}\) + \(\frac{25}{100}\) < 1.
Page No. 551
Question 1.
Draw and label \(\overline{A B}\) in the space at the right.
\(\overline{A B}\) is a __________ .
__________
Answer:
![]()
\(\overline{A B}\) is a line segment.
Draw and label an example of the figure.
Question 2.
\(\underset { XY }{ \longleftrightarrow } \)
Type below:
__________
Answer:
![]()
\(\underset { XY }{ \longleftrightarrow } \) is a line
Question 3.
obtuse ∠K
Type below:
__________
Answer:
Angle K is greater than a right angle and less than a straight angle.
Question 4.
∠CDE
Type below:
__________
Answer:
angle CDE
Use Figure M for 5 and 6.
Question 5.
Name a line segment.
Type below:
__________
Answer:
line segment TU
Explanation:
TU line is a straight path of points that continues without an end in both directions.
Question 6.
Name a right angle.
Type below:
__________
Answer:
Angle TUW
Explanation:
TUW is a right angle that forms a square corner.
Draw and label an example of the figure.
Question 7.
\(\overrightarrow{P Q}\)
Type below:
__________
Answer:
![]()
\(\overrightarrow{P Q}\) is a ray.
Question 8.
acute ∠RST
Type below:
__________
Answer:
Angle RST
Question 9.
straight ∠WXZ
Type below:
__________
Answer:
![]()
Use Figure F for 10–15.
Question 10.
Name a ray.
Type below:
__________
Answer:
Ray K
Explanation:
K is a ray that has one endpoint and continues without an end in one direction.
Question 11.
Name an obtuse angle.
Type below:
__________
Answer:
Angle ABK
Explanation:
ABK is an obtuse angle that is greater than a right angle and less than a straight angle.
Question 12.
Name a line.
Type below:
__________
Answer:
Line AC
Explanation:
AC is a line that is a straight path of points that continues without end in
both directions.
Question 13.
Name a line segment.
Type below:
__________
Answer:
Line Segment PQ
Explanation:
PQ is a line segment that is part of a line between two endpoints.
Question 14.
Name a right angle.
Type below:
__________
Answer:
Angle PRC
Explanation:
PRC is a right angle that forms a square corner.
Question 15.
Name an acute angle.
Type below:
__________
Answer:
Angle ABJ
Explanation:
ABJ is an acute angle that is less than a right angle.
Page No. 552
Use the picture of the bridge for 16 and 17.
Question 16.
Classify ∠A.
_____ angle
Answer:
Right Angle
Explanation:
A is the right angle that forms a square corner.
Question 17.
Which angle appears to be obtuse?
∠ _____
Answer:
∠C
Explanation:
C is an obtuse angle that is greater than a right angle and less than a straight angle.
Question 18.
How many different angles are in Figure X?
List them.
Type below:
__________
Answer:
4 Angles;
Right Angle = Angle EBC;
Obtuse angle = Angle DBF;
Acute angle = Angle DBE;
Straight angle = Angle ABC.
Explanation:
Question 19.
Vanessa drew the angle at the right and named it ∠TRS. Explain why Vanessa’s name for the angle is incorrect. Write a correct name for the angle.
Type below:
__________
Answer:
Vanessa’s name for the angle is incorrect. Because She drew ∠TSR. The two rays R and T have the same endpoint at S called the angle. Also, the TSR is an acute angle that is less than a right angle.
Question 20.
Write the word that describes the part of Figure A.

\(\overline{B G}\) _________
\(\underset { CD }{ \longleftrightarrow } \) _________
∠FBG _________
\(\overrightarrow{B E}\) _________
∠AGD _________
Answer:
\(\overline{B G}\) Line Segment.
\(\underset { CD }{ \longleftrightarrow } \) Line.
∠FBG Right Angle.
\(\overrightarrow{B E}\) Ray.
∠AGD an acute angle.
Conclusion:
We hope the given data about Go Math Grade 4 Answer Key Chapter 9 Relate Fractions and Decimals PDF help you more during the practice sessions. If you want to ask any doubts, feel free to check HMH Go Math Grade 4 Chapter 9 Answer Key Homework Practice FL.
