Everyday Math Grade 5 Answers Unit 1 Area and Volume

Everyday Mathematics 5th Grade Answer Key Unit 1 Area and Volume

Everyday Mathematics Grade 5 Home Link 1.2 Answers

Strategies for Finding Area
Here are two strategies you can use to find the area of a rectangle.

Find the area of each rectangle.
Question 1.

Area = _________ square units
Answer:
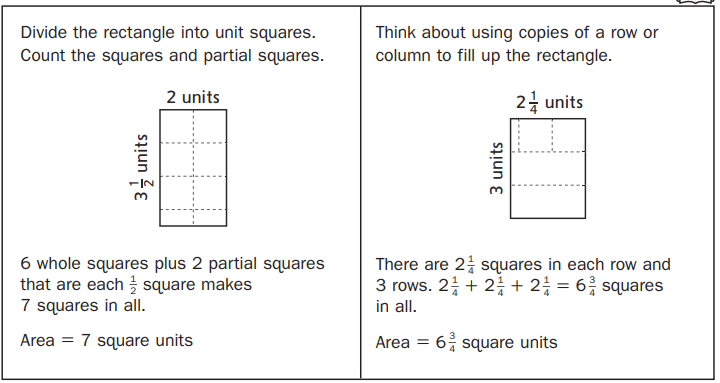
There are 2(1/5) squares in each column and 4 columns.
2(1/5) +2(1/5) +2(1/5) +2(1/5) = 8(4/5) squares in all.
Area = 8(4/5) square units
Explanation:
In the above image, we can observe a rectangle. A rectangle is divided into unit squares. There are 2(1/5) squares in each column. There are 4 columns. An addition sentence is a mathematical expression that shows two or more values added together. Add 2(1/5) squares four times because here 4 columns are there. By adding the squares results in 8(4/5). The area of the rectangle is equal to 8(4/5) square units.

Question 2.

Area = _________ square units
Answer:
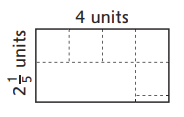
There are 4(1/3) squares in each row and 3 rows.
4(1/3) + 4(1/3) + 4(1/3) = 13 squares in all.
Area = 13 square units
Explanation:
In the above image, we can observe a rectangle. A rectangle is divided into unit squares. There are 4(1/3) squares in each row. There are 3 rows. An addition sentence is a mathematical expression that shows two or more values added together. Add 4(1/3) squares as three times because here 3 rows are there. By adding the squares results in 13. The Area of the rectangle is equal to the 13 square units.

Practice
Solve.
Question 3.
14 – (9 + 2) = _________
Answer:
14 – (9 + 2) = 3
14 – (11) = 3
Explanation:
In the above expression, we can observe two arithmetic operations. One is subtraction and the other is addition.
An addition sentence is a mathematical expression that shows two or more values added together. First, we have to perform the additional operations. By adding these two numbers 9 and 2 we got 11.
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. After performing addition, subtract 11 from 14 then we got 3.

Question 4.
(14 – 9) + 2 = _________
Answer:
(14 – 9) + 2 = 7
(5) + 2 = 7
Explanation:
In the above expression, we can observe two arithmetic operations. One is subtraction and the other is addition.
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. First, we have to perform a subtraction operation. Subtract 9 from 14 then we got 5.
An addition sentence is a mathematical expression that shows two or more values added together. After performing subtraction perform an addition operation. By adding these two numbers 5 and 2 we got 7.

Question 5.
8 + (\(\frac{6}{2}\)) – 1 = _________
Answer:
8 + (6/2) – 1 = 10
8 + 3 – 1 = 10
8 + 2 = 10
Explanation:
In the above expression, we can observe three arithmetic operations. One is addition, division, and subtraction.
The division is a method of distributing a group of things into equal parts. It is one of the four basic operations of arithmetic. First divide (6/2) then we got 3.
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. After performing division perform subtraction operation. Subtract 1 from 3 then we got 2.
An addition sentence is a mathematical expression that shows two or more values added together. After performing subtraction perform an addition operation. By adding these two numbers 8 and 2 we got 10.

Question 6.
\(\frac{(8+6)}{2}\) – 1 =_________
Answer:
[(8 + 6)/2] – 1 = 6
[(14)/2] – 1 = 6
[7] – 1 = 6
Explanation:
In the above expression, we can observe three arithmetic operations. One is addition, division, and subtraction.
An addition sentence is a mathematical expression that shows two or more values added together. First, perform an addition operation. By adding these two numbers 8 and 6 we got 14.
The division is a method of distributing a group of things into equal parts. It is one of the four basic operations of arithmetic. After performing the addition operations perform division. Divide (14/2) then we got 7.
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. After performing division perform subtraction operation. Subtract 1 from 7 then we got 6.

Everyday Math Grade 5 Home Link 1.3 Answer Key

Finding the Area of Rectangles
Find the area of the rectangles below. Write a number sentence for each problem and explain how you found the area.

Question 1.

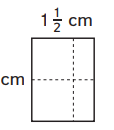
Area = ________
Number sentence: _________
Answer:
There are 1(1/2) squares in each row and 2 rows.
1(1/2) + 1(1/2) = 3 squares in all.
Area = 3 square centimeters.
Number sentence: 1(1/2) + 1(1/2) = 3
Explanation:
In the above image, we can observe a rectangle. A rectangle is divided into unit squares. There are 1(1/2) squares in each row. There are 2 rows. An addition sentence is a mathematical expression that shows two or more values added together. Add 1(1/2) squares as two times because here 2 rows are there. By adding the squares results in 3. The area of the rectangle is equal to the 3 square centimeters.

Question 2.

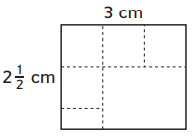
Area = ________
Number sentence: _________
Answer:
There are 2(1/2) squares in each column and 3 columns.
2(1/2) + 2(1/2) + 2(1/2) = (2 + 2 +2)(1/2 +1/2 +1/2) = 7(1/2) squares in all.
Area = 7(1/2) square centimeters.
Number sentence: 2(1/2) + 2(1/2) + 2(1/2) = 7(1/2)
Explanation:
In the above image, we can observe a rectangle. A rectangle is divided into unit squares. There are 2(1/2) squares in each column. There are 3 columns. An addition sentence is a mathematical expression that shows two or more values added together. Add 2(1/2) squares as three times because here 3 rows are there. By adding the squares results in 7(1/2). The area of the rectangle is equal to the 7(1/2) square centimeters.

Practice
Solve.
Question 3.
36 inches = ________ feet
Answer:
1 feet = 12 inches
2 feet = 24 inches
3 feet = 36 inches
36 inches = 3 feet
Explanation:
1 foot is equal to 12 inches. Here we have to find out 36 inches in feet. An addition sentence is a mathematical expression that shows two or more values added together. By adding 12 inches as three times. We got 36 inches. Then 36 inches is equal to 3 feet.

Question 4.
________ inches = 5 feet
Answer:
1 feet = 12 inches
2 feet = 24 inches
3 feet = 36 inches
4 feet = 48 inches
5 feet = 60 inches
60 inches = 5 feet
Explanation:
1 foot is equal to 12 inches. Here we have to find out 5 feet in inches. An addition sentence is a mathematical expression that shows two or more values added together. By adding 12 inches as 5 times. We got 60 inches. Then 60 inches is equal to 5 feet.

Question 5.
18 inches = ________ feet
Answer:
1 feet = 12 inches
1/2 feet = 6 inches
18 inches = 1 1/2 feet
Explanation:
1 foot is equal to 12 inches and 1/2 feet is equal to 6 inches. Here we have to find out 18 inches in feet. An addition sentence is a mathematical expression that shows two or more values added together. Adding 12 inches and 6 inches results in 1(1/2) feet. Then 18 inches is equal to 1(1/2) feet.

Question 6.
\(\frac{1}{2}\) foot = ________ inches
Answer:
1 foot = 12 inches
[1/2] foot = 6 inches
Explanation:
We know that 1 foot is equal to 12 inches. Then 1/2 foot is equal to 6 inches.

Everyday Mathematics Grade 5 Home Link 1.4 Answers

How Many Fields?
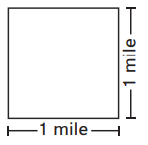
A farmer has one square mile of land.
Question 1.
If he divides his land into square fields that are \(\frac{1}{2}\) mile long and \(\frac{1}{2}\) mile wide, how many fields will he have?
________ fields

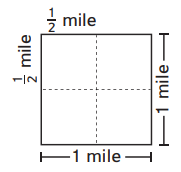
Answer:
In the above image, we can observe four equal square fields.
Explanation:
In the above image, we can observe one square field represents one mile. There are 4 square boxes total. He has 4 fields.

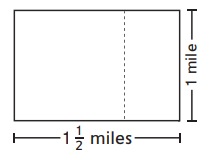
Question 2.
If he divides his land into square fields that are \(\frac{1}{3}\) mile long and \(\frac{1}{3}\) mile wide, how many fields will he have?
___________ fields

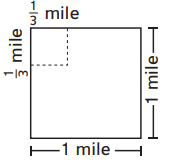
Answer:
He divides his land into square fields that are 1/3 mile long and 1/3 mile wide. In the above image, we can observe 1 mile long and 1 mile wide. [(1/3) + (1/3) + (1/3)] = 1 mile. Here 3(1/3) miles is equal to 1 mile.
Here we have 3 rows and 3 columns. In the 1st row, we have 3 squares. In the 2nd row, we have 3 squares. In the 3rd row, we have 3 squares.
Total number of fields are 3 + 3 + 3 = 9.
Explanation:
In the above image, we can observe 1/3 mile long and 1/3 mile wide. Here we have 3 rows and 3 columns.
First row first column represents [(1/3) +(1/3)] = 2/3.
First row second column represents [(1/3) +(1/3)] = 2/3.
First row third column represents [(1/3) +(1/3)] = 2/3.
In first row we have (2/3) + (2/3) +(2/3) = 6/3 = 3 squares.
In second row we have (2/3) + (2/3) +(2/3) = 6/3 = 3 squares.
In third row we have (2/3) + (2/3) +(2/3) = 6/3 = 3 squares.
Total number of fields are 3 + 3 + 3 = 9 fields.

Question 3.
If he divides his land into square fields that are \(\frac{1}{4}\) mile long and \(\frac{1}{4}\) mile wide, how many fields will he have?
_________ fields

Answer:
He divides his land into square fields that are 1/4 mile long and 1/4 mile wide. In the above image, we can observe 1 mile long and 1 mile wide. [(1/4) + (1/4) + (1/4) + (1/4)] = 1 mile. Here 4(1/4) miles is equal to 1 mile.
Here we have 4 rows and 4 columns. In the 1st row, we have 4 squares. In the 2nd row, we have 4 squares. In the 3rd row, we have 4 squares. In the 4th row, we have 4 squares.
Total number of fields are 4 + 4 + 4 + 4 = 16 Fields.
Explanation:
In the above image, we can observe 1/4 mile long and 1/4 mile wide. Here we have 4 rows and 4 columns. In the 1st row, we have 4 squares. In the 2nd row, we have 4 squares. In the 3rd row, we have 4 squares. In the 4th row, we have 4 squares.
Total number of fields are 4 + 4 + 4 + 4 = 16.

Question 4.
a. Suppose the farmer buys another \(\frac{1}{2}\) square mile of land and divides all his land into square fields \(\frac{1}{4}\) mile long and \(\frac{1}{4}\) mile wide. How many fields will he have?
_______ fields

Answer:
Total area of land = 1 + 1/2 = 3/2 square miles.
Area of square fields = 1/4 x 1/4 = 1/16 square miles.
Number of fields = (3/2)/(1/16) = 24 fields.
Explanation:
The farmer buys another 1/2 square mile of land and divides all his land into square fields 1/4 mile long and 1/4 mile wide. The area of square fields is equal to 1/4 x 1/4 = 1/16 square miles. Total area of land = 1 + 1/2 = 3/2 square miles. The number of fields is equal to 24.

b. What is the total area of his land in square miles?
__________ square miles
Answer:
The total area of his land is 1(1/2) square miles or it can also be written as 3/2 square miles.

Practice
Question 5.
a. _______ min = 1hr
b. 180 min = _______ hr
Answer:
a. 1 min = 60 sec
60 min = 1hr
b. 1 min = 60 sec
60 min = 1hr
120 min = 2hrs
180 min = 3hrs

Explanation:
a. We know that 1 min is equal to 60 sec. 1hr is equal to 60 min.
b. we know that 60 min = 1hr. Then 180 min = 3hrs.

Question 6.
a. 1,000 g = _______ kg
b. _______ g = 4 kg
Answer:
a. 1000 g = 1 kg
b. 1000 g = 1 kg
2000 g = 2 kg
3000 g = 3 kg
4000 g = 4 kg
Explanation:
a. We know that 1,000 g = 1kg.
b. Multiply 1,000 g into 4 times then we got 4,000 g. 4kg is equal to 4,000 g.

Everyday Math Grade 5 Home Link 1.5 Answer Key

Comparing Volumes of Everyday Objects
Find these (or similar) items in your house:
a cereal bowl
a drinking glass
a coffee mug
Question 1.
Which item has the greatest volume? __________
Answer:
When we compare the surface areas of the cereal bowl, drinking class, and a coffee mug,
The order is as follows:
Coffee mug > Cereal bowl > Drinking glass
Hence, from the above,
We can conclude that the Coffee mug has the greatest volume

Question 2.
Which item has the smallest volume? ____________
Answer:
When we compare the surface areas of the cereal bowl, drinking class, and a coffee mug,
The order is as follows:
Coffee mug > Cereal bowl > Drinking glass
Hence, from the above,
We can conclude that the Drinking glass has the smallest volume

Question 3.
Explain your answers to Problems 1 and 2.
Answer:
When we compare the surface areas of the cereal bowl, drinking class, and a coffee mug,
The order is as follows:
Coffee mug > Cereal bowl > Drinking glass

Practice
Find the area of each rectangle.
Question 4.

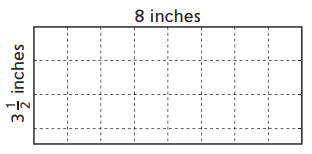
Area = _________ square inches
Answer:
There are 3(1/2) squares in each column and 8 columns.
3(1/2) + 3(1/2) + 3(1/2) + 3(1/2) + 3(1/2) + 3(1/2) + 3(1/2) + 3(1/2) = 24 + 4 = 28 squares in all.
Area = 28 square inches.
Explanation:
In the above image, we can observe a rectangle. A rectangle is divided into square inches. There are 3(1/2) squares in each column. There are 8 columns. An addition sentence is a mathematical expression that shows two or more values added together. Add 3(1/2) squares as 8 times because here 8 columns are there. By adding the squares results in 28. The area of the rectangle is equal to 28 square inches.

Question 5.

Area = _________ in.²
Answer:
The given figure is:

We know that,
The area of the rectangle = Length × Width
So,
The area of the rectangle = 8 × 3\(\frac{1}{2}\)
We know that,
3\(\frac{1}{2}\) = \(\frac{7}{2}\)
So,
The area of the rectangle = 8 × \(\frac{7}{2}\)
= \(\frac{8 × 7}{2}\)
= 28 in²
Hence, from the above,
We can conclude that the area of the rectangle is: 28 in²

Everyday Mathematics Grade 5 Home Link 1.6 Answers

Volume Measurement
Volume is the measure of the amount of space a 3-dimensional object takes up. When we talk about the volume of a container (for example, a vase, a can, a glass, a bowl, a bucket, a box), we are talking about the amount the container can hold.

Only 3-dimensional objects take up space and have volume. Two-dimensional shapes have other attributes that we can measure, such as length and area. But 2-dimensional shapes do not have volume.
Question 1.
Circle each item below that has volume.

Answer:

Explanation:
Volume is the measure of the amount of space a 3-dimensional object takes up. The objects that are having volume are a bar of soap, a baseball, an empty crayon box, a bucket, a swimming pool, a cereal box, the kitchen sink.

Question 2.
Choose one of the items you circled. Describe one way you could measure the volume of that item. Be sure to tell what unit you would use and why.
Answer:
From the circled items,
The item that can be chosen is: A swimming pool
We know that,
The swimming pool is like a shape of a cuboid with the dimensions as follows:
Length of the swimming pool, Width of the swimming pool, and depth or height of the swimming pool
So,
The volume f the swimming pool can be given as:
Volume = Length × Width × Height

Practice
Solve.
Question 3.
(30 + 40) × 5 = ________
Answer:
(30 + 40) × 5 = 350
(70) × 5 = 350
Explanation:
In the above expression, we can observe two arithmetic operations. One is addition and multiplication.
An addition sentence is a mathematical expression that shows two or more values added together. First perform addition operation. By adding these two numbers 30 and 40 we got 70.
Multiplication of two numbers is the repeated addition of one number to the number of times equal to the other number. After performing the addition operations perform multiplication. Multiply 70 and 5 then we got 350.

Question 4.
30 + (40 × 5) = _________
Answer:
30 + (40 × 5) = 230
30 + (200) = 230
Explanation:
In the above expression, we can observe two arithmetic operations. One is addition and multiplication.
Multiplication of two numbers is the repeated addition of one number to the number of times equal to the other number. First, perform a multiplication operation. Multiply 40 and 5 then we got 200.
An addition sentence is a mathematical expression that shows two or more values added together. After performing multiplication operation perform addition operation. By adding these two numbers 30 and 200 we got 230.

Question 5.
(694 – 95) + (2 + 3) = __________
Answer:
(694 – 95) + (2 + 3) = 604
(599) + (5) = 604
Explanation:
In the above expression, we can observe two arithmetic operations. One is addition and subtraction.
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. First, perform subtraction operations. Subtract 95 from 694 then we got 599.
An addition sentence is a mathematical expression that shows two or more values added together. After performing subtraction operation perform addition operation. By adding these two numbers 2 and 3 we got 5. Then add 599 and 5 results 604.

Question 6.
________ = 15 – (12 + 6 – 3)
Answer:
0 = 15 – (12 + 6 – 3)
0 = 15 – (18 – 3)
0 = 15 – (15)
Explanation:
In the above expression, we can observe two arithmetic operations. One is addition and subtraction.
An addition sentence is a mathematical expression that shows two or more values added together. First, perform an addition operation. By adding these two numbers 12 and 6 we got 18.
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. After performing the addition operation perform the subtraction operation. First, subtract 3 from 18 then we got 15. Subtract 15 from 15 then we got 0.

Everyday Math Grade 5 Home Link 1.7 Answer Key

More Cube-Stacking Problems
The cubes in each rectangular prism are the same size. Each prism has at least one stack of cubes that goes up to the top. Find the total number of cubes needed to completely fill each prism. Then find the volume of each prism.
Question 1.

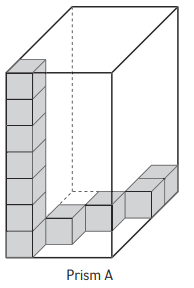
Cubes needed to fill Prism A:
_______ cubes
Volume of Prism A: _______ units³
Answer:

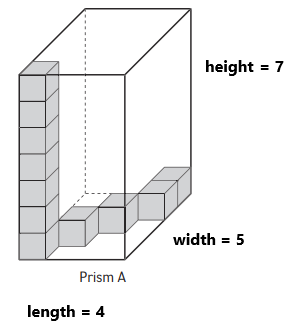
Cubes needed to fill Prism A are 140 cubes.
Volume of Prism A = length x width x height.
Volume of Prism A = 4 x 5 x 7 units³
The volume of Prism A is 140 units³
Explanation:
The cubes in rectangular prism A are the same size. Prism A has one stack of cubes that goes up to the top. The total number of cubes needed to fill prism A is 140 cubes. The volume of prism A contains length, width, height.
The length of prism A is equal to 4 units.
The width of prism A is equal to 5 units.
The height of prism A is equal to 7 units.
Volume of Prism A = length x width x height.
Volume of Prism A = 4 x 5 x 7 units³
The volume of Prism A is 140 units³

Question 2.

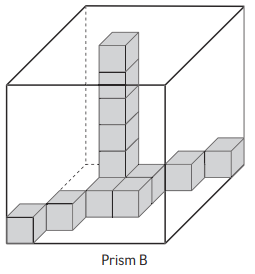
Cubes needed to fill Prism B:
_______ cubes
Volume of Prism B: _______ cubic units
Answer:

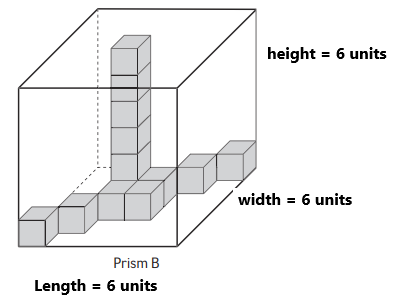
1 layer = 36 cubes.
36 x 6 = 216 cubes.
Cubes needed to fill Prism B is 216 cubes.
Volume of Prism B = length x width x height.
Volume of Prism B = 6 x 6 x 6 units³
The volume of Prism B is 216 units³

Explanation:
The cubes in rectangular prism B are the same size. The prism B has one stack of cubes that goes up to the top. The total number of cubes needed to fill the prism B is 216 cubes. The volume of prism B contains length, width, height.
Length of the prism B is equal to 6 units.
The width of prism B is equal to 6 units.
The height of prism B is equal to 6 units.
Volume of Prism B = length x width x height.
Volume of Prism B = 6 x 6 x 6 units³
The volume of Prism B is 216 units³

Question 3.

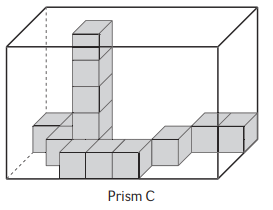
Cubes needed to fill Prism C:
_______ cubes
Volume of Prism C: _______ cubic units
Answer:

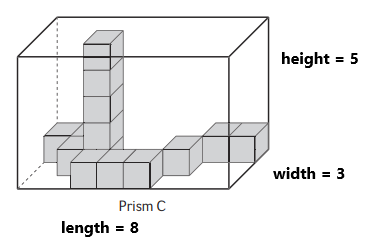
Cubes needed to fill Prism C is 120 cubes.
Volume of Prism C = length x width x height
Volume of Prism C = 8 x 3 x 5 units³
The volume of Prism C is 120 units³
Explanation:
The cubes in rectangular prism C are the same size. The prism C has one stack of cubes that goes up to the top. The total number of cubes needed to fill the prism C is 120 cubes. The volume of prism C contains length, width, height.
The length of the prism C is equal to 6 units.
The width of the prism C is equal to 6 units.
The height of the prism C is equal to 6 units.
Volume of Prism C = length x width x height
Volume of Prism C = 8 x 3 x 5 units³
Volume of Prism C is 120 units³

Practice
Solve.
Question 4.
(14 + 30) × 2 = _______
Answer:
(14 + 30) × 2 = 88
(44) × 2 = 88
Explanation:
In the above expression, we can observe two arithmetic operations. One is addition and multiplication.
An addition sentence is a mathematical expression that shows two or more values added together. First, perform an addition operation. By adding these two numbers 14 and 30 we got 44.
Multiplication of two numbers is the repeated addition of one number to the number of times equal to the other number. After performing the addition operations perform multiplication. Multiply 44 and 2 then we got 88.

Question 5.
14 + (30 × 2) = _______
Answer:
14 + (30 × 2) = 74
14 + (60) = 74
Explanation:
In the above expression, we can observe two arithmetic operations. One is addition and multiplication.
Multiplication of two numbers is the repeated addition of one number to the number of times equal to the other number. First, perform a multiplication operation. Multiply 30 and 2 then we got 60.
An addition sentence is a mathematical expression that shows two or more values added together. After performing multiplication operation perform addition operation. By adding these two numbers 14 and 60 we got 74.

Question 6.
_______ = (68 – 58) × (8 + 8 + 8)
Answer:
240 = (68 – 58) × (8 + 8 + 8)
240 = (10) × (24)
Explanation:
In the above expression, we can observe three arithmetic operations. One is addition, subtraction, and multiplication.
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. First, perform subtraction operations. Subtract 58 from 68 then we got 10.
An addition sentence is a mathematical expression that shows two or more values added together. After performing subtraction operation perform addition operation. By adding these three numbers 8, 8, and 60 we got 24.
Multiplication of two numbers is the repeated addition of one number to the number of times equal to the other number. After performing addition and subtraction operations perform multiplication. Multiply these two numbers 10 and 24 then we got 240.

Question 7.
(15 – 10) + (4 × 5) = _______ + 5
Answer:
(15 – 10) + (4 × 5) = 20 + 5
(5) + (20)= 20 + 5
Explanation:
In the above expression, we can observe three arithmetic operations. One is addition, subtraction, and multiplication.
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. First, perform subtraction operations. Subtract 10 from 15 then we got 5.
Multiplication of two numbers is the repeated addition of one number to the number of times equal to the other number. After performing the subtraction operations perform multiplication. Multiply these two numbers 4 and 5 then we got 20.
An addition sentence is a mathematical expression that shows two or more values added together. After performing subtraction and multiplication operations perform addition operations. By adding these two numbers 5 and 20 we got 25.

Everyday Mathematics Grade 5 Home Link 1.8 Answers

Packing Boxes
A fifth-grade class raised money to buy math tools to send to other schools. Tom, Ed, and Anu are in charge of packing unit cubes. They want each student to receive a box with at least 100 unit cubes.

Tom, Ed, and Anu started packing the boxes. They wonder if each box is big enough to hold at least 100 cubes.

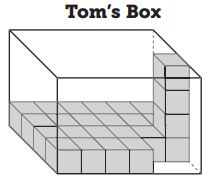
Question 1.
a. How many cubes can Tom’s box hold?
_________ cubes
b. Is Tom’s box big enough? __________
Answer:

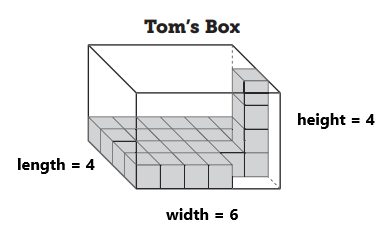
a. Volume = length x width x height = 4 x 6 x 4 = 96 cubes. Tom’s box hold 96 cubes.
b. No, because the Tom’s box doesn’t have 100 cubes.
Explanation:
In the above image, we can observe Tom’s box. The box contains length, width, and height.
The length of the box is 4.
The width of the box is 6.
The height of the box is 4.
Volume = length x width x height = 4 x 6 x 4 = 96 cubes.
Tom’s box holds 96 cubes. They want each student to receive a box with at least 100 unit cubes.
Tom’s box is not big enough. Because Tom’s box doesn’t have 100 cubes.

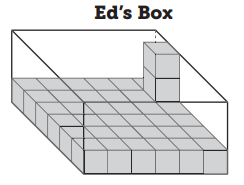
Question 2.
a. How many cubes can Ed’s box hold?
_________ cubes
b. Is Ed’s box big enough? _________
Answer:

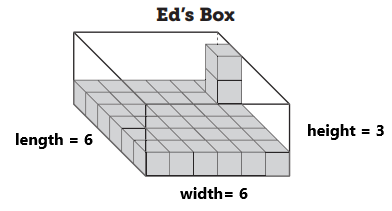
a. Volume = length x width x height = 6 x 6 x 3 = 108 cubes. Ed’s box hold 108 cubes.
b. Yes, because the Ed’s box have at least 100 cubes.
Explanation:
In the above image, we can observe Ed’s box. The box contains length, width, and height.
The length of the box is 6.
The width of the box is 6.
The height of the box is 3.
Volume = length x width x height = 6 x 6 x 3 = 108 cubes.
Ed’s box holds 108 cubes. They want each student to receive a box with at least 100 unit cubes.
Ed’s box is big enough. Because Ed’s box has at least 100 cubes.

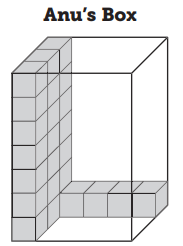
Question 3.
a. How many cubes can Anu’s box hold?
_________ cubes
b. Is Anu’s box big enough? _________
Answer:

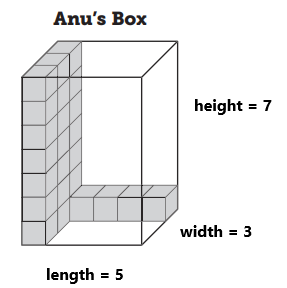
a. Volume = length x width x height = 5 x 3 x 7 = 105 cubes. Anu’s box hold 105 cubes.
b. Yes, because the Anu’s box have at least 100 cubes.
Explanation:
In the above image, we can observe Anu’s box. The box contains length, width, and height.
The length of the box is 5.
The width of the box is 3.
The height of the box is 7.
Volume = length x width x height = 5 x 3 x 7 = 105 cubes.
Anu’s box holds 105 cubes. They want each student to receive a box with at least 100 unit cubes.
Anu’s box is big enough. Because Anu’s box has at least 100 cubes.

Practice
Insert parentheses to make each equation true.
Question 4.
14 + 2 = 6 + 2 × 3 + 2
Answer:
14 + 2 = 6 + 2 × (3 + 2)
16 = 6 + 2 × (5)
16 = 6 + 10
16 = 16
Explanation:
In the above expression, we have to insert parentheses to make each equation true. Here we have to insert parentheses after the multiplication symbol. The numbers that we have to keep parentheses are 3 and 2. Then the equation is true.

Question 5.
16 – 5 × 4 = 22 × 2
Answer:
(16 – 5) × 4 = 22 × 2
(11) × 4 = 44
44 = 44
Explanation:
In the above expression, we have to insert parentheses to make each equation true. Here we have to insert parentheses before the multiplication symbol. The numbers that we have to keep parentheses are 16 and 5. Then the equation is true.

Question 6.
16 × 10 = 100 + 220 ÷ 2
Answer:
16 x 10 = (100 + 220) ÷ 2
160 = (320) ÷ 2
160 = 160
Explanation:
In the above expression, we have to insert parentheses to make each equation true. Here we have to insert parentheses before the division symbol. The numbers that we have to keep parentheses are 100 and 220. Then the equation is true.

Question 7.
3 × 56 – 4 = 128 + 28
Answer:
3 ∗ (56 – 4) = 128 +28
3 ∗ (52) = 156
156 = 156
Explanation:
In the above expression, we have to insert parentheses to make each equation true. Here we have to insert parentheses after the multiplication symbol. The numbers that we have to keep parentheses are 56 and 4. Then the equation is true.

Everyday Math Grade 5 Home Link 1.9 Answer Key

Comparing Volumes
Today you learned two different formulas to find the volume of a rectangular prism:
V = l × w × h (volume = length × width × height)
V = B × h (volume = area of the base × height)
Use the formulas to find the volume of each prism. Be sure to include a unit. Cross out the prism in each set that has a volume different than the other prisms.
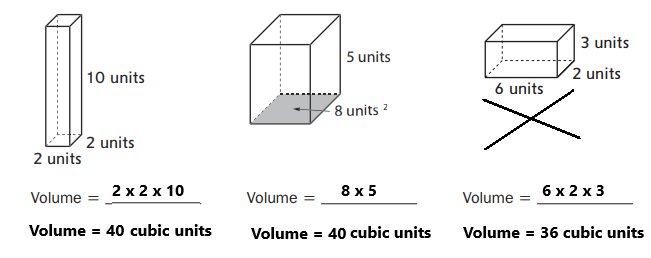
Question 1.
Set 1

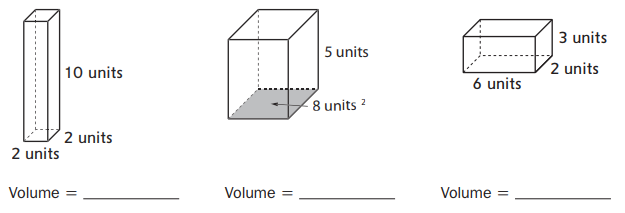
Answer:

Explanation:
In the above image, we can observe three different types of prisms. For the above three prisms, we have to find the volume.
V = l × w × h (volume = length × width × height)
V = B × h (volume = area of the base × height)
1. The first prism contains length, width, and height. Length = 2 units, width = 2 units, height = 10 units.
The volume of a rectangular prism = length x width x height.
Volume = 2 x 2 x 10
Volume = 40 cubic units.

2. The second prism contains an area of the base and height. Area of the base = 8 square units, height = 5 units.
The volume of a rectangular prism = Area of the base × Height
Volume = 8 x 5
Volume = 40 cubic units.

3. The third prism contains length, width, and height. Length = 6 units, width = 2 units, height = 3 units.
The volume of a rectangular prism = length x width x height.
Volume = 6 x 2 x 3
Volume = 36 cubic units.
Cross out the third prism because the third prism volume is different from other prisms volume.

Question 2.
Set 2

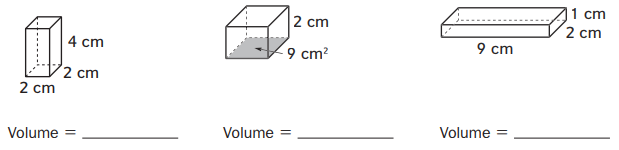
Answer:

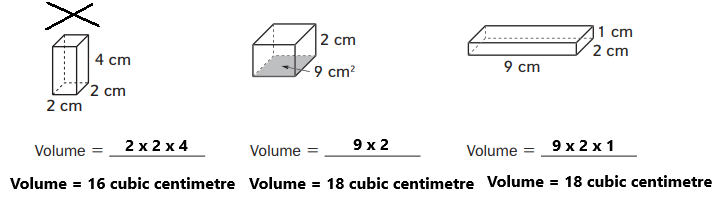
Explanation:
In the above image, we can observe three different types of prisms. For the above three prisms, we have to find the volume.
V = l × w × h (volume = length × width × height)
V = B × h (volume = area of the base × height)

1. The first prism contains length, width, and height. Length = 2 cm, width = 2 cm, height = 4 cm.
The volume of a rectangular prism = length x width x height.
Volume = 2 x 2 x 4
Volume = 16 cubic centimeter.

2. The second prism contains the area of the base and height. Area of the base = 9 square centimeter, height = 2 centimeter.
The volume of a rectangular prism = Area of the base × Height
Volume = 9 x 2
Volume = 18 cubic centimeter.

3. The third prism contains length, width, and height. Length = 9 centimeter, width = 2 centimeter, height = 1 centimeter.
The volume of a rectangular prism = length x width x height.
Volume = 9 x 2 x 1
Volume = 18 cubic centimeter.
Cross out the first prism because the first prism volume is different from other prisms volume.

Practice
Find the area of each rectangle.
Question 3.

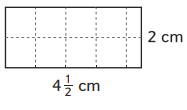
Area = _________
Answer:
There are 4(1/2) squares in each row and 2 rows.
4(1/2) + 4(1/2) = 8 + [(1/2) +(1/2)] = 9 squares in all.
Area = 9 square centimeters.
Explanation:
In the above image, we can observe a rectangle. A rectangle is divided into unit squares. There are 4(1/2) squares in each row. There are 2 rows. An addition sentence is a mathematical expression that shows two or more values added together. Add 4(1/2) squares as two times, because here 2 rows are there. By adding the squares results in 9. The area of the rectangle is equal to 9 square centimeters.

Question 4.

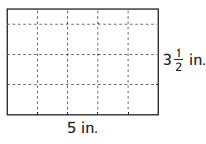
Area = __________
Answer:
There are 3(1/2) squares in each column and 5 columns.
3(1/2) + 3(1/2) + 3(1/2) + 3(1/2) + 3(1/2) = 15 + [(1/2) +(1/2) +(1/2) + (1/2) + (1/2)] = 17(1/2) squares in all.
Area = 17(1/2) square inches.
Explanation:
In the above image, we can observe a rectangle. A rectangle is divided into unit squares. There are 3(1/2) squares in each column. There are 5 columns. An addition sentence is a mathematical expression that shows two or more values added together. Add 3(1/2) squares as five times, because here 5 columns are there. By adding the squares results in 17(1/2). The area of the rectangle is equal to 17(1/2) square inches.

Everyday Mathematics Grade 5 Home Link 1.10 Answers

Comparing Volume Units
Circle the volume unit that is larger.
Question 1.
cubic centimeters cubic meters
Answer:

Explanation:
We know that,
1 cubic meter = 10 ⁶ centimeters
1 cubic centimeter = 10 ^-6 meters
So,
“Cubic meters” is larger

Question 2.
cubic millimeters cubic inches
Answer:

Question 3.
cubic miles cubic decimeters
Answer:

Question 4.
cubic meters cubic feet
Answer:

Question 5.
Explain how you knew which volume unit was larger in Problems 1–4.
Answer:
The unit that is the longer length is the larger volume unit. Because the volume unit is a cube that has the length, width, and height of that length unit.

Find an object around your home that you might measure with the given unit.
Question 6.
cubic inches
Answer:
The object around your home that you might measure with cubic inches is: High-pressure bottles

Question 7.
cubic meters
Answer:
The object around your home that you might measure with cubic meters is: Bathtub

Question 8.
cubic feet
Answer:
The object around your home that you might measure with cubic feet is: Any room in a house

Practice
Find the volume of a rectangular prism with the given dimensions.
Question 9.
length = 8 meters
height = 5 meters
width = 2 meters
________ meters³
Answer:
The volume of the rectangular prism (v) = length x width x height
v = 8meters x 2 meters x 5 meters
v = 80 meters³

Question 10.
area of the base = 25 inches³
height = 4 inches
________ inches³
Answer:
The volume of the rectangular prism (v) = Area of the base x height
v= 25 inches³x 4 inches
v = 100 inches³

Everyday Math Grade 5 Home Link 1.11 Answer Key

Finding Volumes
Find the volume of each figure below. Then name at least one real-world object that the figure could model. For example, the figure in Problem 1 could model a flashlight.
Question 1.

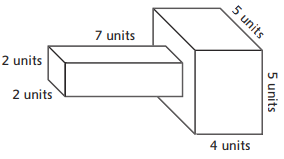
Volume = _________ cubic units
This figure could model …
Answer:
The given figure is:

From the given figure,
We can observe that the figure is made up of two 3-d objects i.e., two cuboids
So,
To find the volume of the total figure,
We have to add the volume of two cuboids
We know that,
The volume of cuboid = Length × Width × Height
So,
The volume of the figure = (7 ×2 × 2) + (5 × 5 × 4)
= 28 + 100
= 128 cubic units
Hence, from the above figure,
We can conclude that the given figure could model a: Flashlight or a microphone

Question 2.

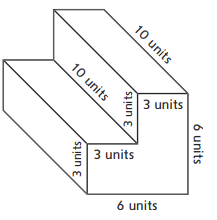
Volume = _________ cubic units
This figure could model …
Answer:
The given figure is:

From the given figure,
We can observe that the given figure is made up of three 3-d figures i.e., 2 cuboids and 1 cuboid like shape
We know that,
The volume of cuboid = Length × Width × Height
The volume of cuboid like figure = Width × Length × Height
So,
the volume of the cuboid figure = (3 × 3 × 10) + (3 × 3 × 10) + (3 × 3 × 10)
= 270 cubic units
Hence, from the above figure,
We can conclude that the given figure could model a couch or stairs

Question 3.

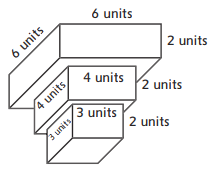
Volume = _________ cubic units
This figure could model …
Answer:
The given figure is:

From the given figure,
We can observe that the given figure is made up of three 3-d figures i.e., cuboids
We know that,
The volume of cuboid = Length × Width × Height
So,
The total volume of the given figure = (6 × 6 × 2) + (4 × 4 × 2) + (3 × 3 × 2)
= 72 + 32 + 18
= 122 cubic units
Hence, from the above figure,
We can conclude that the given figure could model a cup or a vase

Everyday Math Grade 5 Home Link 1.12 Answer Key

Playing Prism Pile-Up
Three rounds of Prism Pile-Up are shown below. For each round:

• Find the volume of each figure.
• Circle the winning card (the card with the figure that has a greater volume).
• Write one or more number sentences for the winning card.

Round 1

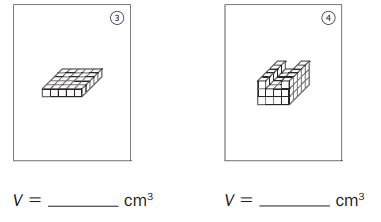
Number sentence(s): ____________
Answer:

Round 2

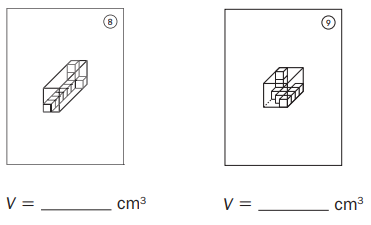
Number sentence(s): ____________
Answer:
We know that,
The volume of the prism = Base Area × Height
= Length × Width × Height
The number of cubes in a prism indicates the volume of the prism
So,
For Fig 8,
The volume of the prism = 7 × 3 × 2 = 42 cm³
For Fig 9,
The volume of the prism = 3 × 3 × 4 = 36 cm³
Hence, from the above,
We can conclude that the volume of Fig 8 is greater

Round 3

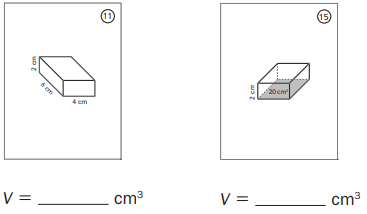
Number sentence(s): ____________
Answer:
We know that,
The volume of prism = Base Area × Height
= Length × Width × Height
So,
For Fig 11,
The volume of prism = 6 ×4 × 2 = 48 cm³
For Fig 15,
The volume of prism = 20 × 2 = 40 cm³
Hence, from the above,
We can conclude that the volume of fig 11 is greater