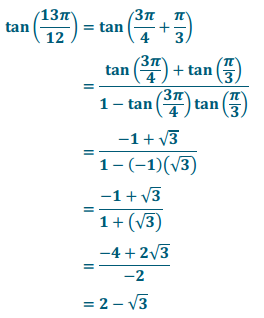Eureka Math Precalculus Module 4 Lesson 3 Answer Key

Engage NY Eureka Math Precalculus Module 4 Lesson 3 Answer Key

Eureka Math Precalculus Module 4 Lesson 3 Example Answer Key

Example 1.
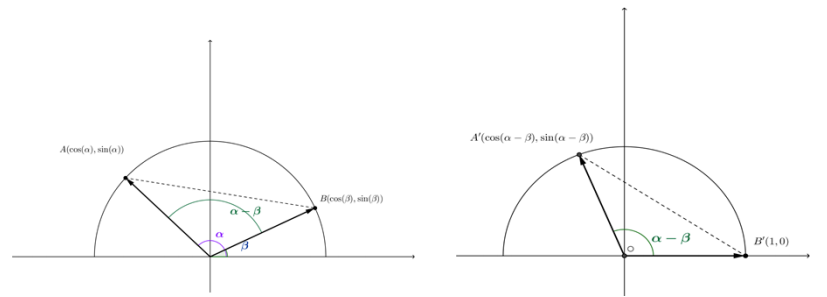
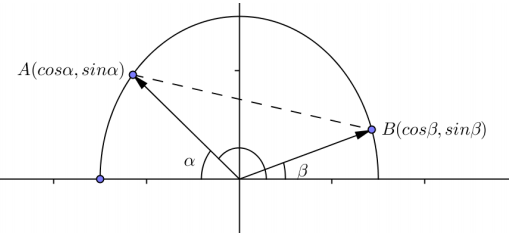
Consider the figures below. The figure on the right is obtained from the figure on the left by rotating by – β about the origin.

Answer:
a. Calculate the length of \(\overline{A B}\) in the figure on the left.
Answer:

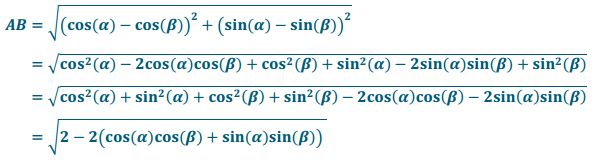
b. Calculate the length of \(\overline{A}^{\prime} {B}^{\prime}\) in the figure on the right.
Answer:

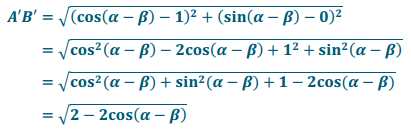
c. Set AB and A’B’ equal to each other, and solve the equation for cos(α – β).
Answer:

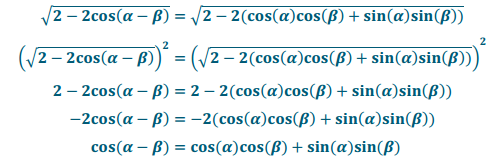
Example 2.
Use the identity tan(θ) = \(\frac{\sin (\theta)}{\cos (\theta)}\) to show that tan(α + β) = \(\frac{\tan (\alpha) + \tan (\beta)}{1 – \tan (\alpha) \tan (\beta)}\).
Answer:

Eureka Math Precalculus Module 4 Lesson 3 Exercise Answer Key

Exercises 1–2
Exercises 1.
Use the fact that cos( – θ) = cos(θ) to determine a formula for cos(α + β).
Answer:
cos(α + β) = cos(α – β)
= cos(α)cos( – β) + sin(α)sin( – β)
= cos(α)cos(β) + sin(α)( – sin(β))
= cos(α)cos(β) – sin(α)sin(β)

Exercises 2.
Use the fact that sin(θ) = cos(\(\frac{\pi}{2}\) – θ) to determine a formula for sin(α – β).
Answer:
sin(α – β) = cos⁡(\(\frac{\pi}{2}\) – (α – β))
= cos⁡((\(\frac{\pi}{2}\) – α) + β)
= cos(\(\frac{\pi}{2}\) – α) cos⁡(β) – sin(\(\frac{\pi}{2}\) – α) sin⁡(β)
= sin(α)cos(β) – cos(α)sin(β)

Exercises 3–5
Exercises 3.
Verify the identity tan(α – β) = \(\frac{\tan (\alpha) – \tan (\beta)}{1 + \tan (\alpha) \tan (\beta)}\) for all (α – β)≠\(\frac{\pi}{2}\) + πn.
Answer:

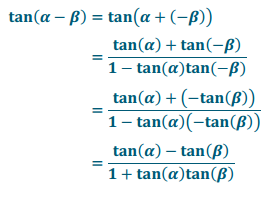
Exercises 4.
Use the addition and subtraction formulas to evaluate the expressions shown.
a. cos( – \(5\frac{\pi}{12}\))
Answer:
cos( – \(\frac{5\pi}{12}\)) = cos(\(\frac{\pi}{4}\) – \(\frac{2\pi}{3}\))
= cos(\(\frac{\pi}{4}\))cos(\(\frac{2\pi}{3}\)) + sin(\(\frac{\pi}{4}\))sin(\(\frac{2\pi}{3}\))
= \(\frac{\sqrt{2}}{2}\) (\(\frac{ – 1}{2}\)) + \(\frac{\sqrt{2}}{2}\) (\(\frac{\sqrt{3}}{2}\))
= \(\frac{\sqrt{6} – \sqrt{2}}{4}\)

b. sin(\(\frac{23\pi}{12}\))
Answer:
sin(\(\frac{23\pi}{12}\)) = sin(\(\frac{9\pi}{4}\) – \(\frac{\pi}{3}\))
= sin(\(\frac{9\pi}{4}\))cos(\(\frac{\pi}{3}\)) – sin(\(\frac{\pi}{3}\))cos(\(\frac{9\pi}{4}\))
= \(\frac{\sqrt{2}}{2}\) (\(\frac{1}{2}\)) – \(\frac{\sqrt{3}}{2}\) (\(\frac{\sqrt{2}}{2}\))
= \(\frac{\sqrt{2} – \sqrt{6}}{4}\)

c. tan(\(\frac{5\pi}{12}\))
Answer:

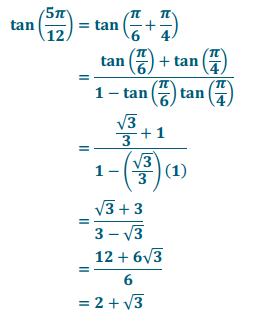
Exercises 5.
Use the addition and subtraction formulas to verify these identities for all real – number values of θ.
a. sin(π – θ) = sin(θ)
Answer:
sin(π – θ) = sin(π)cos(θ) – sin(θ)cos(π) = 0(cos(θ)) – sin(θ)( – 1) = sin(θ)

b. cos(π + θ) = – cos(θ)
Answer:
cos(π + θ) = cos(π)cos(θ) – sin(π)sin(θ) = – 1(cos(θ)) – 0(sin(θ)) = – cos(θ)

Eureka Math Precalculus Module 4 Lesson 3 Problem Set Answer Key

Question 1.
Use the addition and subtraction formulas to evaluate the given trigonometric expressions.
a. cos(\(\frac{\pi}{12}\))
Answer:
cos(\(\frac{\pi}{12}\)) = cos(\(\frac{\pi}{3}\) – \(\frac{\pi}{4}\))
= cos(\(\frac{\pi}{3}\))cos(\(\frac{\pi}{4}\)) + sin(\(\frac{\pi}{3}\))sin(\(\frac{\pi}{4}\))
= \(\frac{1}{2}\)∙\(\frac{\sqrt{2}}{2}\) + \(\frac{\sqrt{3}}{2}\)∙\(\frac{\sqrt{2}}{2}\)
= \(\frac{\sqrt{2} + \sqrt{6}}{4}\)

b. sin(\(\frac{\pi}{12}\))
Answer:
sin(\(\frac{\pi}{12}\)) = sin(\(\frac{\pi}{3}\) – \(\frac{\pi}{4}\))
= sin(\(\frac{\pi}{3}\))cos(\(\frac{\pi}{4}\)) – cos(\(\frac{\pi}{3}\))sin(\(\frac{\pi}{4}\))
= \(\frac{\sqrt{3}}{2}\)∙\(\frac{\sqrt{2}}{2}\) – \(\frac{1}{2}\)∙\(\frac{\sqrt{2}}{2}\)
= \(\frac{\sqrt{6} – \sqrt{2}}{4}\)

c. sin(5\(\frac{\pi}{12}\))
Answer:
sin(5\(\frac{\pi}{12}\)) = sin(\(\frac{\pi}{6}\) + \(\frac{\pi}{4}\))
= sin(\(\frac{\pi}{6}\))cos(\(\frac{\pi}{4}\)) + cos(\(\frac{\pi}{6}\))sin(\(\frac{\pi}{4}\))
= \(\frac{1}{2}\)∙\(\frac{\sqrt{2}}{2}\) + \(\frac{\sqrt{3}}{2}\)∙\(\frac{\sqrt{2}}{2}\)
= \(\frac{\sqrt{2} + \sqrt{6}}{4}\)

d. cos( – \(\frac{\pi}{12}\))
Answer:
cos( – \(\frac{\pi}{12}\)) = cos(\(\frac{\pi}{4}\) – \(\frac{\pi}{3}\))
= cos(\(\frac{\pi}{4}\))cos(\(\frac{\pi}{3}\)) + sin(\(\frac{\pi}{4}\))sin(\(\frac{\pi}{3}\))
= \(\frac{\sqrt{2}}{2}\)∙\(\frac{1}{2}\) + \(\frac{\sqrt{2}}{2}\)∙\(\frac{\sqrt{3}}{2}\)
= \(\frac{\sqrt{2} + \sqrt{6}}{4}\)

e. sin(\(\frac{7\pi}{12}\))
Answer:
sin(\(\frac{7\pi}{12}\)) = sin(\(\frac{\pi}{4}\) + \(\frac{\pi}{3}\))
= sin(\(\frac{\pi}{4}\))cos(\(\frac{\pi}{3}\)) + cos(\(\frac{\pi}{4}\))sin(\(\frac{\pi}{3}\))
= \(\frac{\sqrt{2}}{2}\)∙\(\frac{1}{2}\) + \(\frac{\sqrt{2}}{2}\)∙\(\frac{\sqrt{3}}{2}\)
= \(\frac{\sqrt{2} + \sqrt{6}}{4}\)

f. cos( – \(7\frac{\pi}{12}\))
Answer:
cos( – \(\frac{7\pi}{12}\)) = cos( – \(\frac{\pi}{4}\) – \(\frac{\pi}{3}\))
= cos( – \(\frac{\pi}{4}\))cos(\(\frac{\pi}{3}\)) + sin( – \(\frac{\pi}{4}\))sin(\(\frac{\pi}{3}\))
= \(\frac{\sqrt{2}}{2}\)∙\(\frac{1}{2}\) – \(\frac{\sqrt{2}}{2}\)∙\(\frac{\sqrt{3}}{2}\)
= \(\frac{\sqrt{2} – \sqrt{6}}{4}\)

g. sin(\(\frac{13\pi}{12}\))
Answer:
sin(\(\frac{13\pi}{12}\)) = sin(\(\frac{3\pi}{4}\) + \(\frac{\pi}{3}\))
= sin(\(\frac{3\pi}{4}\))cos(\(\frac{\pi}{3}\)) + cos(\(\frac{3\pi}{4}\))sin(\(\frac{\pi}{3}\))
= \(\frac{\sqrt{2}}{2}\)∙\(\frac{1}{2}\) – \(\frac{\sqrt{2}}{2}\)∙\(\frac{\sqrt{3}}{2}\)
= \(\frac{\sqrt{2} – \sqrt{6}}{4}\)

h. cos( – \(\frac{13\pi}{12}\))
Answer:
cos( – \(\frac{13\pi}{12}\)) = cos( – \(\frac{\pi}{4}\) – \(\frac{\pi}{3}\))
= cos( – \(\frac{\pi}{4}\))cos(\(\frac{\pi}{3}\)) + sin( – \(\frac{\pi}{4}\))sin(\(\frac{\pi}{3}\))
= \(\frac{\sqrt{2}}{2}\)∙\(\frac{1}{2}\) – \(\frac{\sqrt{2}}{2}\)∙\(\frac{\sqrt{3}}{2}\)
= \(\frac{\sqrt{2} – \sqrt{6}}{4}\)

i. sin(\(\frac{\pi}{12}\))cos(\(\frac{\pi}{12}\)) + cos(\(\frac{\pi}{12}\))sin(\(\frac{\pi}{12}\))
Answer:
sin(\(\frac{\pi}{12}\))cos(\(\frac{\pi}{12}\)) + cos(\(\frac{\pi}{12}\))sin(\(\frac{\pi}{12}\)) = sin(\(\frac{\pi}{6}\))
= \(\frac{1}{2}\)

j. sin(\(\frac{5\pi}{12}\))cos(\(\frac{\pi}{6}\)) – cos(\(\frac{5\pi}{12}\))sin(\(\frac{\pi}{6}\))
Answer:
sin(\(\frac{5\pi}{12}\))cos(\(\frac{\pi}{6}\)) – cos(\(\frac{5\pi}{12}\))sin(\(\frac{\pi}{6}\)) = sin(\(\frac{\pi}{4}\))
= \(\frac{\sqrt{2}}{2}\)

k. sin\(\frac{\pi}{8}\))cos\(\frac{\pi}{8}\)) + cos\(\frac{\pi}{8}\))sin\(\frac{\pi}{8}\))
Answer:
sin\(\frac{\pi}{8}\))cos\(\frac{\pi}{8}\)) + cos\(\frac{\pi}{8}\))sin\(\frac{\pi}{8}\)) = sin(\(\frac{\pi}{4}\))
= \(\frac{\sqrt{2}}{2}\)

l. cos\(\frac{\pi}{8}\))cos\(\frac{\pi}{8}\)) – sin\(\frac{\pi}{8}\))sin\(\frac{\pi}{8}\))
Answer:
cos\(\frac{\pi}{8}\))cos\(\frac{\pi}{8}\)) – sin\(\frac{\pi}{8}\))sin\(\frac{\pi}{8}\)) = cos(\(\frac{\pi}{4}\))
= \(\frac{\sqrt{2}}{2}\)

m. cos(\(\frac{\pi}{4}\))cos(\(\frac{\pi}{12}\)) + sin(\(\frac{\pi}{4}\))sin(\(\frac{\pi}{12}\))
Answer:
cos(\(\frac{\pi}{4}\))cos(\(\frac{\pi}{12}\)) + sin(\(\frac{\pi}{4}\))sin(\(\frac{\pi}{12}\)) = cos(\(\frac{\pi}{6}\))
= \(\frac{\sqrt{3}}{2}\)

n. sin(π/3)cos(\(\frac{\pi}{12}\)) – cos(π/3)sin(\(\frac{\pi}{12}\))
Answer:
sin(π/3)cos(\(\frac{\pi}{12}\)) – cos(π/3)sin(\(\frac{\pi}{12}\)) = sin(\(\frac{\pi}{4}\))
= \(\frac{\sqrt{2}}{2}\)

Question 2.
Figure 2 is obtained from Figure 1 by rotating the angle by α about the origin.
Use the method shown in Example 1 to show that cos(α + β) = cos(α)cos(β) – sin(α)sin(β).
Figure 1

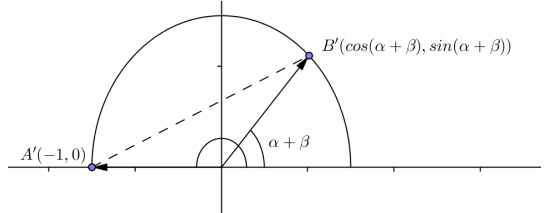
Figure 2

Answer:
AB = \(\sqrt{(\cos (\beta) – \cos (\alpha))^{2} + (\sin (\beta) – \sin (\alpha))^{2}}\)
A’B’ = \(\sqrt{(\cos (\alpha + \beta) – ( – 1))^{2} + (\sin (\alpha + \beta) – 0)^{2}}\)
AB = A’B’
\(\left(\sqrt{(\cos (\beta) – \cos (\alpha))^{2} + (\sin (\beta) – \sin (\alpha))^{2}}\right)^{2}\) = \(\left(\sqrt{(\cos (\alpha + \beta) – ( – 1))^{2} + (\sin (\alpha + \beta) – 0)^{2}}\right)^{2}\)
(cos(β) – cos(α))² + (sin(β) – sin(α))² = (cos(α + β) – ( – 1))² + (sin(α + β) – 0)²
cos² (β) – 2 cos(β)cos(α) + cos² (α) + sin² (β) – 2 sin(β)sin(α) + sin² (α) = cos² (α + β) + 2 cos(α + b) + 1 + sin² (α + β)
2 – 2cos(β)cos(α) – 2sin(β)sin(α) = 2 + 2 cos(α + β)
– cos(β)cos(α) – sin(β)sin(α) = cos(α + β)
cos(α)cos(β) – sin(α)sin(β) = cos(α + β)

Question 3.
Use the sum formula for sine to show that sin(α – β) = sin(α)cos(β) – cos(α)sin(β).
Answer:
sin(α – β) = sin(α + ( – β)) = sin(α)cos( – β) + cos(α)sin( – β) = sin(α)cos(β) – cos(α)sin(β)

Question 4.
Evaluate tan(α + β) = \(\frac{\sin (\alpha + \beta)}{\cos (\alpha + \beta)}\) to show tan(α + β) = \(\frac{\tan (\alpha) + \tan (\beta)}{1 – \tan (\alpha) \tan (\beta)}\). Use the resulting formula to show that tan(2α) = \(\frac{2 \tan (\alpha)}{1 – \tan ^{2}(\alpha)}\).
Answer:

Question 5.
Show tan(α – β) = \(\frac{\tan (\alpha) – \tan (\beta)}{1 + \tan (\alpha) \tan (\beta)}\).
Answer:

Question 6.
Find the exact value of the following by using addition and subtraction formulas.
a. tan(\(\frac{\pi}{12}\))
Answer:

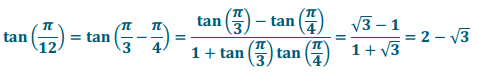
b. tan( – \(\frac{\pi}{12}\))
Answer:

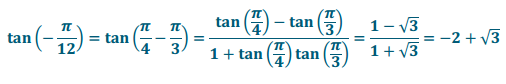
c. tan(\(\frac{7\pi}{12}\))
Answer:

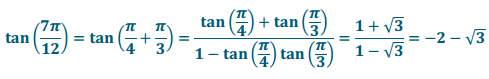
d. tan( – \(\frac{13\pi}{12}\))
Answer:

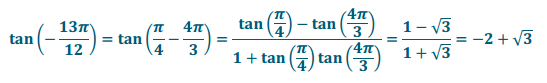
e. \(\frac{\tan \left(\frac{\pi}{4}\right) + \tan \left(\frac{\pi}{12}\right)}{1 – \tan \left(\frac{\pi}{4}\right) \tan \left(\frac{\pi}{12}\right)}\)
Answer:

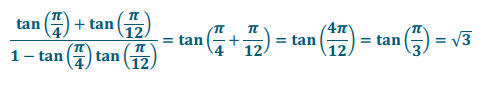
f. \(\frac{\tan \left(\frac{\pi}{3}\right) – \tan \left(\frac{\pi}{12}\right)}{1 + \tan \left(\frac{\pi}{3}\right) \tan \left(\frac{\pi}{12}\right)}\)
Answer:

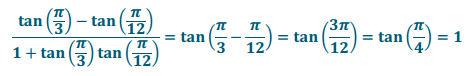
g. \(\frac{\tan \left(\frac{\pi}{12}\right) + \tan \left(\frac{\pi}{12}\right)}{1 – \tan \left(\frac{\pi}{12}\right) \tan \left(\frac{\pi}{12}\right)}\)
Answer:

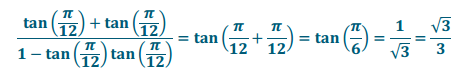
Eureka Math Precalculus Module 4 Lesson 3 Exit Ticket Answer Key

Question 1.
Prove that sin⁡(α + β) = sin⁡(α) cos⁡(β) + sin⁡(β)cos(α).
Answer:
sin(α + β) = sin(α – ( – β))
= sin(α)cos( – β) – sin( – β)cos(α)
= sin(α)cos(β) – ( – sin(β))(cos(α))
= sin(α)cos(β) + sin(β)cos(α)

Question 2.
Use the addition and subtraction formulas to evaluate the given trigonometric expressions.
a. sin(\(\frac{\pi}{12}\))
Answer:

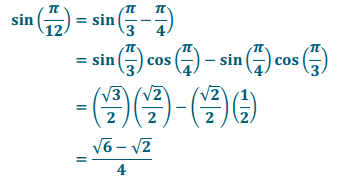
b. tan(\(\frac{13\pi}{12}\))
Answer: