Engage NY Eureka Math Precalculus Module 2 Lesson 3 Answer Key
Eureka Math Precalculus Module 2 Lesson 3 Exercise Answer Key
Opening Exercise
The subway and bus line network connecting four cities that we used in Lesson 2 is shown below. The bus routes connecting the cities are represented by solid lines, and the subway routes are represented by dashed lines.
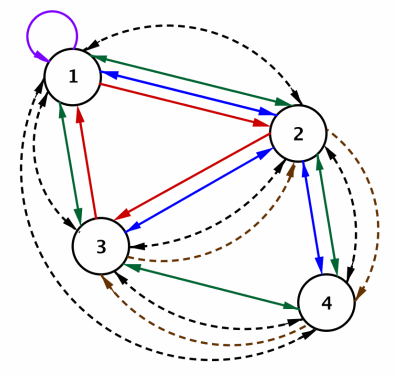
Suppose we want to travel from City 2 to City 1, first by bus and then by subway, with no more than one connecting stop.
a. Complete the chart below showing the number of ways to travel from City 2 to City 1 using first a bus and then the subway. The first row has been completed for you.
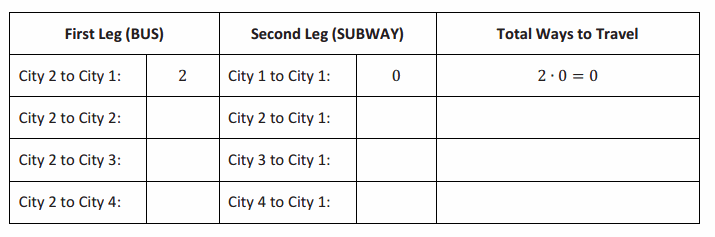
Answer:
b. How many ways are there to travel from City 2 to City 1, first on a bus and then on a subway? How do you know?
Answer:
The total number of ways is the sum of the numbers in the last column. There are 4 ways.
Exploratory Challenge/Exercises 1–12: The Meaning of Matrix Multiplication
Suppose we want to travel between all cities, traveling first by bus and then by subway, with no more than one connecting stop.
Exercise 1.
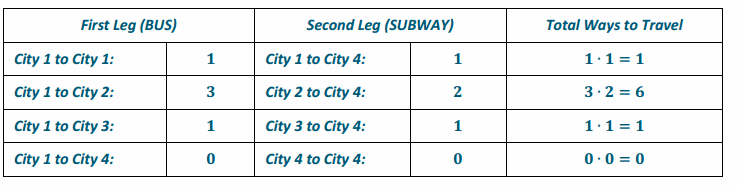
Use a chart like the one in the Opening Exercise to help you determine the total number of ways to travel from
Answer:
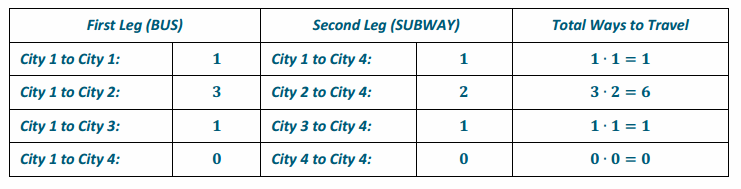
Summing the entries in the last column shows that there are 8 different ways to travel from City 1 to City 4 using first a bus and then the subway.
Exercise 2.
Suppose we create a new matrix P to show the number of ways to travel between the cities, first by bus and then by subway, with no more than one connecting stop. Record your answers to Opening Exercise, part (b) and Exercise 1 in this matrix in the appropriate row and column location. We do not yet have enough information to complete the entire matrix. Explain how you decided where to record these numbers in the matrix shown below.

Answer:
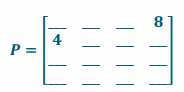
If the rows represent the starting city and the columns represent the destination city, then the ways to travel from City 2 to City 1 would be p2,1, and the ways to travel from City 1 to City 4 would be p1,4.
At this point, circulate around the room to check for understanding by making sure that groups are recording the correct entries in the proper locations in the matrix. Debrief as a whole class if a majority of students are struggling. Consider reviewing matrix notation, especially since students are going to use it in upcoming exercises. For example, if P is a matrix, then p_(i,j) is the element in the ith row and jth column of the matrix. In Exercise 5, some groups may continue to use a table, while some may simply create a list. Make sure that students are recording a written explanation of how they calculated their answers. If students can describe the process of multiplying and summing verbally or in writing, then they are able to calculate the product of two matrices without difficulty.
Exercise 3.
What is the total number of ways to travel from City 3 to City 2 first by bus and then by subway with no more than one connecting stop? Explain how you got your answer and where you would record it in matrix P above.
Answer:
Find the ways to travel by bus from City 3 to each of the other cities, including City 3 itself. Then for each city, find the ways to travel by subway from that city to City 2. Multiply the number of ways from City 3 to the connecting city by the number of ways from the connecting city to City 2. Finally, add the result of the number of ways through each connecting city.
City 3 to City 2 via City 1: 2∙1=2
City 3 to City 2 via City 2: 1∙0=0
City 3 to City 2 via City 3: 0∙2=0
City 3 to City 2 via City 4: 1∙1=1
There are 2+0+0+1=3 ways to travel from City 3 to City 2, using first a bus and then the subway. This would be entered in the 3rd row and 2nd column of matrix P.
Recall matrix B, which shows the number of bus lines connecting the cities in this transportation network, and matrix S, which represents the number of subway lines connecting the cities in this transportation network.
B=\(\left[\begin{array}{llll}
1 & 3 & 1 & 0 \\
2 & 0 & 2 & 2 \\
2 & 1 & 0 & 1 \\
0 & 2 & 1 & 0
\end{array}\right]\) and S=\(\left[\begin{array}{llll}
0 & 1 & 1 & 1 \\
1 & 0 & 1 & 2 \\
1 & 2 & 0 & 1 \\
1 & 1 & 2 & 0
\end{array}\right]\)
Exercise 4.
What does the product b1,2 s2,4 represent in this situation? What is the value of this product?
Answer:
The product b1,2 s2,4 represents the number of ways to travel from City 1 to City 4 via City 2, first by bus and then by subway.
b1,2 s2,4=3∙2=6
Exercise 5.
What does b1,4 s4,4 represent in this situation? What is the value of this product? Does this make sense?
Answer:
The product b1,4 s4,4 represents the number of ways to travel from City 1 to City 4 via City 4, first by bus and then by subway.
b1,4 s4,4=0∙0=0
Since there is no bus route from City 1 to City 4 and no subway route from City 4 to City 4, it is impossible to travel from City 1 to City 4 using first a bus and then a subway. Thus, there are no possible routes.
Exercise 6.
Calculate the value of the expression b1,1 s(1,4)+b(1,2) s(2,4)+b(1,3)s(3,4)+b(1,4) s(4,4). What is the meaning of this expression in this situation?
b(1,1) s(1,4)+b(1,2) s(2,4)+b(1,3)s(3,4)+b(1,4) s(4,4)=1∙1+3∙2+1∙1+0∙0=8
Thus, there are 8 total ways to travel from City 1 to City 4 via any one of the cities, first by bus and then by subway.
Exercise 7.
Circle the first row of B and the second column of S. How are these entries related to the expression above and your work in Exercise 1?
Answer:
We multiplied the first element in the row by the first element in the column, the second by the second, third by third and so on, and then we found the sum of those products. This is the same as the sum of the entries in the last column of the table in Exercise 1.
Exercise 8.
Write an expression that represents the total number of ways you can travel between City 2 and City 1, first by bus and then by subway, with no more than one connecting stop. What is the value of this expression? What is the meaning of the result?
Answer:
b(2,1) s(1,1)+b(2,2) s(2,1)+b(2,3) s(3,1)+b(2,4) s(4,1)=2∙0+0∙1+2∙1+2∙1=4
Thus, there are 4 total ways to travel from City 2 to City 1 via any one of the cities, first by bus and then by subway.
Exercise 9.
Write an expression that represents the total number of ways you can travel between City 4 and City 1, first by bus and then by subway, with no more than one connecting stop. What is the value of this expression? What is the meaning of the result?
Answer:
b(4,1) s(1,1)+b(4,2) s(2,1)+b(4,3) s(3,1)+b(4,4) s(4,1)=0∙0+2∙1+1∙1+0∙1=3
Thus, there are 3 total ways to travel from City 4 to City 1 via any one of the cities, first by bus and then by subway.
Exercise 10.
Complete matrix P that represents the routes connecting the four cities if you travel first by bus and then by subway.
Answer:
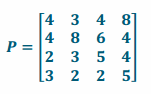
Exercise 11.
Construct a matrix M that represents the routes connecting the four cities if you travel first by subway and then by bus.
Answer:
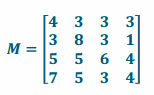
Exercise 12.
Should these two matrices be the same? Explain your reasoning.
Answer:
This transportation network has different numbers of routes connecting cities in each direction. Traveling from
City 1 to City 4 does not have the same number of options as traveling from City 4 to City 1. Therefore, the order in which you select your method of travel makes a difference, which is why the matrices M and P are not equal.
Exercises 13–16
Let A=\(\left[\begin{array}{ccc}
2 & 3 & -1 \\
0 & 1 & 2 \\
1 & 0 & 0
\end{array}\right]\)
a. Construct a matrix Z such that A+Z=A. Explain how you got your answer.
Answer:
Z=\(\left[\begin{array}{lll}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right]\)
We would need to add 0 to each element of A to get the same matrix, so each element of Z must be equal to 0. Also, Z must have the same dimensions as A so we can add corresponding elements.
b. Explain why k∙Z=Z for any real number k.
Answer:
Any number multiplied by 0 is equal to 0. Scalar multiplication multiplies each element of Z by k.
c. The real number 0 has the properties that a+0=0 and a∙0=0 for all real numbers a. Why would mathematicians call Z a zero matrix?
Answer:
The matrix Z has the same properties in matrix addition as the real number 0 has with real number addition.
Exercise 14.
Suppose each city had a trolley car that ran a route between tourist destinations. The blue loops represent the trolley car routes. Remember that straight lines indicate bus routes, and dotted lines indicate subway routes.
Answer:
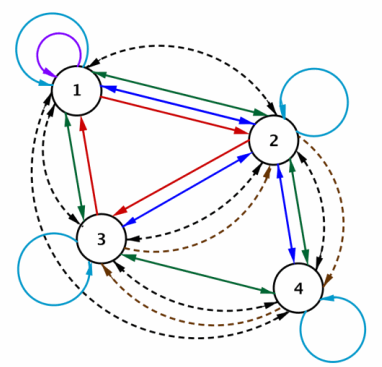
a. Explain why the matrix I shown below would represent the number of routes connecting cities by trolley car in this transportation network.
Answer:
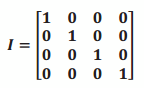
It shows that you can travel on the trolley from City 1 to City 1, City 2 to City 2, City 3 to City 3, and City 4 to City 4 but not between cities.
b. Recall that B is the bus route matrix. Show that I∙B=B. Explain why this makes sense in terms of the transportation network.
Answer:
The entries in matrix I∙B represent the number of ways to travel from city to city, first on a trolley and then on the bus. Since there is only one way in each city to travel by trolley and there are no ways to travel by trolley between cities, the number of routes is the same as the number of bus routes.
c. The real number 1 has the property that 1∙a=a for all real numbers a, and we call 1 the multiplicative identity. Why would mathematicians call I an identity matrix?
Answer:
Matrix I has the same property under matrix multiplication that the real number 1 does for real number multiplication, so it makes sense to call I an identity matrix.
d. What would be the form of a 2×2 identity matrix? What about a 3×3 identity matrix?
Answer:
A 2×2 identity matrix would be I=\(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\), and a 3×3 identity matrix would be I=\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\).
Exercise 15.
In this lesson you learned that the commutative property does not hold for matrix multiplication. This exercise asks you to consider other properties of real numbers applied to matrix arithmetic.
a. Is matrix addition associative? That is, does (A+B)+C=A+(B+C) for matrices A, B, and C that have the same dimensions? Explain your reasoning.
Answer:
Yes. Because all three matrices have the same dimensions, we add corresponding entries. The entries are real numbers. Since the associative property holds for adding real numbers, it would make sense to hold for the addition of matrices.
b. Is matrix multiplication associative? That is, does (A∙B)∙C=A∙(B∙C) for matrices A, B, and C for which the multiplication is defined? Explain your reasoning.
Answer:
Yes. As long as the dimensions of the matrices are such that the multiplications are all defined, computing the products requires that we add and multiply real numbers. Since these operations are associative for real numbers, multiplication is associative for matrices. It would be like finding the number of routes if we had three modes of transportation and changed modes twice. We can count those totals in different groupings as long as we maintain the order of the transportation modes (e.g., bus to subway to train).
c. Is matrix addition commutative? That is, does A+B=B+A for matrices A and B with the same dimensions?
Answer:
Yes, because addition of the individual elements is commutative.
Exercise 16.
Complete the graphic organizer to summarize your understanding of the product of two matrices.

Answer:
Eureka Math Precalculus Module 2 Lesson 3 Problem Set Answer Key
Question 1.
Let A=\(\left[\begin{array}{ll}
1 & 3 \\
2 & 0
\end{array}\right]\) and B=\(\left[\begin{array}{ll}
1 & 2 \\
4 & 3
\end{array}\right]\) represent the bus routes of two companies between 2 cities. Find the product A∙B, and explain the meaning of the entry in row 1, column 2 of A∙B in the context of this scenario.
Answer:
The product is A∙B=\(\left[\begin{array}{ll}
1 & 3 \\
2 & 0
\end{array}\right] \cdot\left[\begin{array}{ll}
1 & 2 \\
4 & 3
\end{array}\right]\)=\(\left[\begin{array}{cc}
13 & 11 \\
2 & 4
\end{array}\right]\). The entry in row 1, column 2 to 11, which means that there are 11 possible routes from the first city to the second city, taking first a bus from Company A and then a bus from Company B.
Question 2.
Let A=\(\left[\begin{array}{lll}
1 & 3 & 2 \\
3 & 1 & 2 \\
4 & 3 & 2
\end{array}\right]\) and B=\(\left[\begin{array}{lll}
2 & 1 & 3 \\
2 & 2 & 1 \\
1 & 3 & 1
\end{array}\right]\) represent the bus routes of two companies between three cities.
a. Let C=A∙B. Find matrix C, and explain the meaning of entry c1,3.
Answer:
The product is C=\(\left[\begin{array}{ccc}
10 & 13 & 8 \\
10 & 11 & 12 \\
16 & 16 & 17
\end{array}\right]\), and c1,3=8 means that there are 8 different ways to travel to City 3 from City 1 by taking a bus from Company A and then a bus from Company B.
b. Nina wants to travel from City 3 to City 1 and back home to City 3 by taking a direct bus from Company A on the way to City 1 and a bus from Company B on the way back home to City 3. How many different ways are there for her to make this trip?
Answer:
Nina wants to travel from City 3 to City 1 and back to City 3, a(3,1)∙b1,3=4∙3=12 means that she has
12 ways to make the trip.
c. Oliver wants to travel from City 2 to City 3 by taking first a bus from Company A and then taking a bus from Company B. How many different ways can he do this?
Answer:
Since C=A∙B=\(\left[\begin{array}{ccc}
10 & 13 & 8 \\
10 & 11 & 12 \\
16 & 16 & 17
\end{array}\right]\), and Oliver wants to travel from City 2 to City 3, he has c(2,3)=12 ways to make the trip.
d. How many routes can Oliver choose from if he travels from City 2 to City 3 by first taking a bus from Company B and then taking a bus from Company A?
Answer:
Since B∙A=\(\left[\begin{array}{ccc}
17 & 16 & 12 \\
12 & 11 & 10 \\
14 & 9 & 10
\end{array}\right]\), and the entry in row 2 , column 3 is 10, which means that there are 10 ways to get from City 2 to City 3 by taking a bus from Company B first and then a bus from Company A.
Question 3.
Recall the bus and trolley matrices from the lesson:
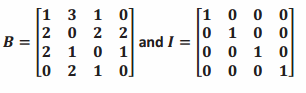
a. Explain why it makes sense that BI=IB in the context of the problem.
Answer:
Since there is only one way to take a trolley in each city, no matter whether you take the trolley before you take the bus or if you take the bus first, the result is the same number of ways as there are bus routes.
b. Multiply out BI and IB to show BI=IB.
Answer:
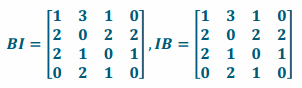
c. Consider the multiplication that you did in part (b). What about the arrangement of the entries in the identity matrix causes BI=B?
Answer:
When you multiply BI, you are multiplying the rows of B by the columns of I; since every entry in the columns of I but the row that you are currently multiplying by is 0, you only get a single value of B to carry over, and it is carried over in the same position. A similar thing happens with IB, but this time it is because the rows of the identity are zero everywhere except at the position you want to carry over.
Question 4.
Consider the matrices
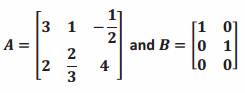
a. Multiply AB and BA or explain why you cannot.
Answer:
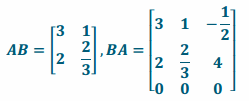
b. Would you consider B to be an identity matrix for A? Why or why not?
Answer:
No. AB has all of the same entries as A for those entries that AB has, but A possesses an additional column that AB does not. BA possesses all of the same entries as A for those that exist in A, but it also possesses a row of zeros that did not exist in A; all three matrices have different dimensions.
c. Would you consider I2=\(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\) or I3=\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\) an identity matrix for A? Why or why not?
Answer:
Answers may vary. It is true that I2 A=A and AI3=A, but neither of these can commute with A based on their dimensions. We can say that I2 is an identity for A on the left, and I3 is an identity for A on the right.
Question 5.
We’ve shown that matrix multiplication is generally not commutative, meaning that as a general rule for two matrices A and B, A∙B≠B∙A. Explain why F∙G=G∙F in each of the following examples.
a. F=\(\left[\begin{array}{ll}
1 & 3 \\
2 & 0
\end{array}\right]\), G=\(\left[\begin{array}{ll}
2 & 6 \\
4 & 0
\end{array}\right]\)
Answer:
We see that F∙G=\(\left[\begin{array}{cc}
14 & 6 \\
4 & 12
\end{array}\right]\) and G∙F=\(\left[\begin{array}{cc}
14 & 6 \\
4 & 12
\end{array}\right]\). Because G=2F, we have
F∙G=F∙(2F)=2(F∙F)=(2F)∙F=G∙F.
b. F=\(\left[\begin{array}{lll}
1 & 3 & 2 \\
3 & 1 & 2 \\
4 & 3 & 2
\end{array}\right]\), G=\(\left[\begin{array}{lll}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right]\)
Answer:
We see that F∙G=\(\left[\begin{array}{lll}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right]\) and G∙F=\(\left[\begin{array}{lll}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right]\). The matrix G is the zero matrix, and any matrix multiplied by a zero matrix will result in the zero matrix.
c. F=\(\left[\begin{array}{lll}
1 & 3 & 2 \\
3 & 1 & 2 \\
4 & 3 & 2
\end{array}\right]\), G=\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)
Answer:
We see that F∙G=\(\left[\begin{array}{lll}
1 & 3 & 2 \\
3 & 1 & 2 \\
4 & 3 & 2
\end{array}\right]\) and G∙F=\(\left[\begin{array}{lll}
1 & 3 & 2 \\
3 & 1 & 2 \\
4 & 3 & 2
\end{array}\right]\). The matrix G is an identity matrix. Any square matrix multiplied by an identity matrix will result in the original matrix.
d. F=\(\left[\begin{array}{lll}
1 & 3 & 2 \\
3 & 1 & 2 \\
4 & 3 & 2
\end{array}\right]\), G=\(\left[\begin{array}{lll}
3 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 3
\end{array}\right]\)
Answer:
We see that F∙G=\(\left[\begin{array}{ccc}
3 & 9 & 6 \\
9 & 3 & 6 \\
12 & 9 & 6
\end{array}\right]\) and G∙F=\(\left[\begin{array}{ccc}
3 & 9 & 6 \\
9 & 3 & 6 \\
12 & 9 & 6
\end{array}\right]\). Because G=3I, we have F∙G=F∙(3I)=3(F∙I)=3(I∙F)=(3I)∙F=G∙F.
Question 6.
Let In be the n×n identity matrix. For the matrices given below, perform each of the following calculations or explain why the calculation is not possible:
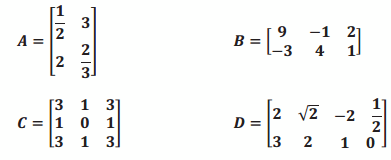
a. AB
Answer:
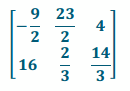
b. BA
Answer:
These matrices have incompatible dimensions multiplied this way.
c. AC
Answer:
A has 2 columns, and C has 3 rows, which means we cannot multiply them.
d. ABC
Answer:
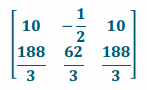
e. ABCD
Answer:
Matrix ABC is a 2×3 matrix, and matrix D is a 2×4 matrix, which means we cannot multiply them.
f. AD
Answer:
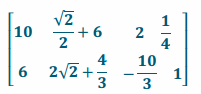
g. A2
Answer:
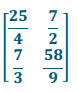
h. C2
Answer:
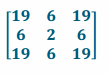
i. BC2
Answer:
\(\left[\begin{array}{ccc}
203 & 64 & 203 \\
-14 & -4 & -14
\end{array}\right]\)
j. ABC+AD
Answer:
ABC and AD have different dimensions, so they cannot be added.
k. ABI2
Answer:
B is 2×3 and I2 is 2×2, so they cannot be multiplied in this order.
l. AI2B
Answer:
This is the same as
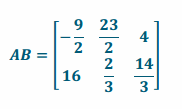
m. CI3B
Answer:
CI3=C, so this is CB, but these have incompatible dimensions and cannot be multiplied.
n. I2BC
Answer:
This is the same as
BC=\(\left[\begin{array}{lll}
32 & 11 & 32 \\
-2 & -2 & -2
\end{array}\right]\)
o. 2A+B
Answer:
2A and B have different dimensions, so they cannot be added.
p. B(I3+C)
Answer:
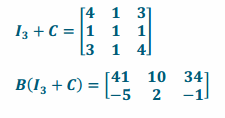
q. B+BC
Answer:
\(\left[\begin{array}{ccc}
41 & 10 & 34 \\
-5 & 2 & -1
\end{array}\right]\)
r. 4DI4
Answer:
\(\left[\begin{array}{cccc}
8 & 4 \sqrt{2} & -8 & 2 \\
12 & 8 & 4 & 0
\end{array}\right]\)
Question 7.
Let F be an m×n matrix. Then what do you know about the dimensions of matrix G in the problems below if each expression has a value?
a. F+G
Answer:
G must have the exact same dimensions as F in order to add them together. That is, the dimensions of G are m×n.
b. FG
Answer:
Here we know that the rows of G must be the same as the columns of F; that is, G has n rows.
c. GF
Answer:
We know that G has m columns.
d. FHG for some matrix H.
Answer:
We know nothing about the dimensions of matrix G based on the dimensions of F.
Question 8.
Consider an m×n matrix A such that m≠n. Explain why you cannot evaluate A2.
Answer:
The only way to evaluate A2 is to multiply AA, which implies that A has the same number of rows as it does columns. Since m≠n, then A2 does not exist.
Question 9.
Let 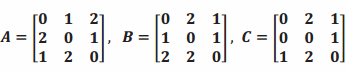 represent the routes of three airlines A, B, and C between three cities.
represent the routes of three airlines A, B, and C between three cities.
a. Zane wants to fly from City 1 to City 3 by taking Airline A first and then Airline B second. How many different ways are there for him to travel?
Answer:
Since A∙B=\(\left[\begin{array}{lll}
5 & 4 & 1 \\
2 & 6 & 2 \\
2 & 2 & 3
\end{array}\right]\), and the entry in row 1, column 3 is 1, there is only 1 way for Zane to travel.
b. Zane did not like Airline A after the trip to City 3, so on the way home, Zane decides to fly Airline C first and then Airline B second. How many different ways are there for him to travel?
Answer:
Since C∙B=\(\left[\begin{array}{lll}
4 & 2 & 2 \\
2 & 2 & 0 \\
2 & 2 & 3
\end{array}\right]\), and the entry in row 3, column 1 is 2, there are 2 ways for Zane to travel.
Question 10.
Let A=\(\left[\begin{array}{llll}
0 & 1 & 1 & 2 \\
1 & 0 & 2 & 1 \\
2 & 1 & 0 & 2 \\
1 & 2 & 1 & 0
\end{array}\right]\) represent airline flights of one airline between 4 cities.
a. We use the notation A2 to represent the product A∙A. Calculate A2. What do the entries in matrix A2 represent?
Answer:
We see that A2=\(\left[\begin{array}{llll}
5 & 5 & 4 & 3 \\
5 & 5 & 2 & 6 \\
3 & 6 & 6 & 5 \\
4 & 2 & 5 & 6
\end{array}\right]\). The entry in row i, column j of matrix A2 is the number of ways to get from City i to City j with one stop in between at one of the other cities.
b. Jade wants to fly from City 1 to City 4 with exactly one stop. How many different ways are there for her to travel?
Answer:
Since (A2))(1,4)=3, Jade can choose between 3 different ways to travel.
c. Now Jade wants to fly from City 1 to City 4 with exactly two stops. How many different ways are there for her to choose?
Answer:
Since A3=A2∙A=\(\left[\begin{array}{llll}
16 & 15 & 18 & 23 \\
15 & 19 & 21 & 19 \\
23 & 19 & 20 & 24 \\
18 & 21 & 14 & 20
\end{array}\right]\), and (A3)(1,4)=23, there are 23 different ways for Jade to travel.
Eureka Math Precalculus Module 2 Lesson 3 Exit Ticket Answer Key
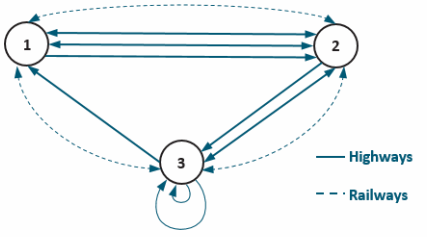
Matrix A represents the number of major highways connecting three cities. Matrix B represents the number of railways connecting the same three cities.
A=\(\left[\begin{array}{lll}
0 & 3 & 0 \\
2 & 0 & 2 \\
1 & 1 & 2
\end{array}\right]\) and B=\(\left[\begin{array}{lll}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}\right]\)
a. Draw a network diagram for the transportation network of highways and railways between these cities. Use solid lines for highways and dotted lines for railways.
Answer:
Question 2.
Calculate and interpret the meaning of each matrix in this situation.
a. A∙B
Answer:
AB=\(\left[\begin{array}{lll}
3 & 0 & 3 \\
2 & 4 & 2 \\
3 & 3 & 2
\end{array}\right]\) It indicates the number of ways to get around between three cities by taking highways
first and then railways second.
b. B∙A
BA=\(\left[\begin{array}{lll}
3 & 1 & 4 \\
1 & 4 & 2 \\
2 & 3 & 2
\end{array}\right]\) It indicates the number of ways to get around between three cities by taking railways first
and then highways second.
Question 3.
In this situation, why does it make sense that A∙B≠B∙A?
Answer:
It makes sense because both transportation networks have a different number of routes connecting cities in each direction. Not every route goes both directions. For example, there are a different number of possible routes from City 1 to City 2 than from City 2 to City 1.