Engage NY Eureka Math Precalculus Module 2 Lesson 24 Answer Key
Eureka Math Precalculus Module 2 Lesson 24 Exercise Answer Key
Opening Exercise
Two particles are moving in a coordinate plane. Particle 1 is at the point \(\left(\begin{array}{l}
1 \\
1
\end{array}\right)\) and moving along the velocity vector \(\left(\begin{array}{c}
– 2 \\
1
\end{array}\right)\). Particle 2 is at the point \(\left(\begin{array}{c}
– 1 \\
1
\end{array}\right)\) and moving along the velocity vector \(\left(\begin{array}{l}
1 \\
2
\end{array}\right) .\). Are the two particles going to collide? If so, at what point, and at what time? Assume that time is measured in seconds.
Answer:
Particle 1: \(\left(\begin{array}{l}
x(t) \\
y(t)
\end{array}\right)\) = \(\left(\begin{array}{l}
1 \\
– 4
\end{array}\right) + \left(\begin{array}{l}
– 2 \\
1
\end{array}\right) t\) x(t) = 1 – 2t, and y(t) = 1 + t y = \(\frac{3}{2} – \frac{1}{2} x\)
Particle 2: \(\left(\begin{array}{l}
x(t) \\
y(t)
\end{array}\right)\) = \(\left(\begin{array}{c}
– 1 \\
1
\end{array}\right) + \left(\begin{array}{l}
1 \\
2
\end{array}\right) t\) x(t) = – 1 + t, and y(t) = 1 + 2t y = 3 + 2x
The particles will not collide. While they do cross the same point at \(\), they do not cross this point at the same time. Particle 1 crosses this point at t = 0.4, and Particle 2 does not cross this point until t = 0.8.
Exercise 1 .
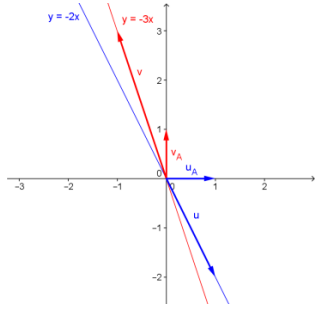
Consider lines l = {(x,y)│〈x,y〉 = t〈1, – 2〉 } and m = {(x,y)│〈x,y〉 = t〈 – 1,3〉 }.
a. To what graph does each line correspond?
Answer:
Line l corresponds to the graph of y = – 2x. Line m corresponds to the graph of y = – 3x.
b. Describe what happens to the vectors defining these lines under the transformation A = \(\left(\begin{array}{ll}
3 & 1 \\
2 & 1
\end{array}\right)\).
Answer:
Each vector is mapped to a new vector. 〈1, – 2〉→〈1,0〉, and 〈 – 1,3〉→〈0,1〉.
c. Show this transformation graphically.
Answer:
The vector that defined l shown in the diagram is u = 〈1, – 2〉, and the vector that defined m shown in the diagram is v = 〈 – 1,3〉. In the diagram, the image of l, when transformed by A, results in the graph of the line y = 0,’ and the image of m, when transformed by A, results in the graph of the line x = 0.
Exercise 2.
Consider lines l = {(x,y)│〈x,y〉 = 〈1,1〉 + t〈1, – 2〉} and m = {(x,y)│〈x,y〉 = 〈1,1〉 + t〈 – 1,3〉}.
a. What is the solution to the system of equations given by lines l and m?
Answer:
The solution is (1,1).
b. Describe what happens to the lines under the transformation A = \(\left(\begin{array}{ll}
3 & 1 \\
2 & 1
\end{array}\right)\).
Answer:
Line l becomes Al = {(x,y)│〈x,y〉 = 〈4,3〉 + t〈1,0〉}.
Line m becomes Am = {(x,y)│〈x,y〉 = 〈4,3〉 + t〈0,1〉}.
c. What is the solution to the system of equations after the transformation?
Answer:
The solution is the point (4,3).
Exercise 3.
The system of equations is given below. A graph of the equations and their intersection point is also shown.
x + y = 6
x – y = 2
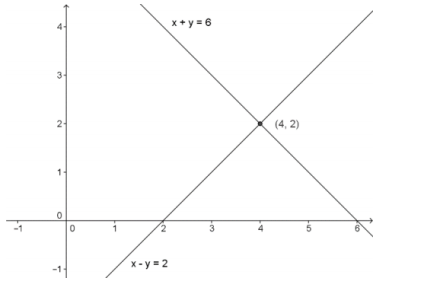
a. Write each line in the form L(t) = p + vt where p is the position vector whose terminal point is the solution of the system and v is the velocity vector that defines the path of a particle traveling along the line such that when t = 0, the solution to the system is (x(0),y(0)).
Answer:
L1 (t) = \(\left(\begin{array}{l}
4 \\
2
\end{array}\right) + \left(\begin{array}{c}
– 1 \\
1
\end{array}\right) t\)
L2 (t) = \(\left(\begin{array}{l}
4 \\
2
\end{array}\right) + \left(\begin{array}{l}
1 \\
1
\end{array}\right) t\)
b. Describe a translation that takes the point (x(0),y(0)) to the origin. What is the new system?
Answer:
Translate the system by the vector 〈 – 4, – 2〉.
y = – x
y = x
c. Describe a transformation matrix A that rotates the lines to the x – and y – axes. What is the new system?
Answer:
Let A = \(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\). We want A∙\(\left(\begin{array}{c}
– 1 \\
1
\end{array}\right)\) = \(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\), and A∙\(\left(\begin{array}{l}
1 \\
1
\end{array}\right)\) = \(\left(\begin{array}{l}
0 \\
1
\end{array}\right)\). Thus
– a + b = 1
– c + d = 0
and
a + b = 0
c + d = 1
Solving for a, b, c, and d gives
A = \(\left(\begin{array}{cc}
– \frac{1}{2} & \frac{1}{2} \\
\frac{1}{2} & \frac{1}{2}
\end{array}\right)\)
The new system is
x = 0
y = 0
d. Describe a translation that results in a system that has the same solution set as the original system. What is the new system of equations?
Answer:
Translate by the vector 〈4,2〉. The new system is
x = 4
y = 2,
which does intersect at the point (4,2), so the solution is (4,2).
Eureka Math Precalculus Module 2 Lesson 24 Problem Set Answer Key
Question 1.
Consider the system of equations \(\left\{\begin{array}{c}
y = 3 x + 2 \\
y = – x + 14
\end{array}\right.\).
a. Solve the system of equations.
Answer:
The point (3,11) is a simultaneous solution to the two equations.
b. Ilene wants to rotate the lines representing this system of equations about their solution and wishes to apply the matrix \(\left(\begin{array}{cc}
\cos (\theta) & – \sin (\theta) \\
\sin (\theta) & \cos (\theta)
\end{array}\right)\)to any point A on either of the lines. If Ilene is correct, then applying a rotation to the solution will map the solution to itself. Let θ = 90°, and find where Ilene’s strategy maps the solution you found in part (a). What is wrong with Ilene’s strategy?
Answer:
\(\left(\begin{array}{cc}
\cos \left(90^{\circ}\right) & – \sin \left(90^{\circ}\right) \\
\sin \left(90^{\circ}\right) & \cos \left(90^{\circ}\right)
\end{array}\right)\left(\begin{array}{c}
3 \\
11
\end{array}\right)\) = \(\left(\begin{array}{cc}
0 & – 1 \\
1 & 0
\end{array}\right)\left(\begin{array}{c}
3 \\
11
\end{array}\right)\)
= \(\left(\begin{array}{c}
– 11 \\
3
\end{array}\right)\)
Her transformation does not map the pivot point to itself, so the system is not rotating around the pivot point.
c. Jasmine thinks that in order to apply a rotation to some point on either of these two lines, the entire system needs to be shifted so that the pivot point is translated to the origin. For an arbitrary point A on either of the two lines, what transformation needs to be applied so that the pivot point is mapped to the origin?
Answer:
To map the pivot point to the origin, we can take a translation equal to the opposite of the pivot point. In this case, that means for A = \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\)on either of the two lines, we do the following: \(\left(\begin{array}{l}
x \\
y
\end{array}\right) + \left(\begin{array}{c}
– 3 \\
– 11
\end{array}\right)\).
We see that \(\left(\begin{array}{c}
3 \\
11
\end{array}\right) + \left(\begin{array}{c}
– 3 \\
– 11
\end{array}\right)\) = \(\left(\begin{array}{l}
0 \\
0
\end{array}\right)\).
d. After applying your transformation in part (c), apply Ilene’s rotation matrix for θ = 90°. Show that the pivot point remains on the origin. What happens to the point (0,2) after both of these transformations?
Answer:
\(\left(\begin{array}{cc}
0 & – 1 \\
1 & 0
\end{array}\right)\left(\begin{array}{l}
0 \\
0
\end{array}\right)\) = \(\left(\begin{array}{l}
0 \\
0
\end{array}\right)\)
\(\left(\begin{array}{cc}
0 & – 1 \\
1 & 0
\end{array}\right)\left(\left(\begin{array}{l}
0 \\
2
\end{array}\right) + \left(\begin{array}{c}
– 3 \\
– 11
\end{array}\right)\right)\) = \(\left(\begin{array}{cc}
0 & – 1 \\
1 & 0
\end{array}\right)\left(\begin{array}{l}
– 3 \\
– 9
\end{array}\right)\)
= \(\left(\begin{array}{c}
9 \\
– 3
\end{array}\right)\)
The point is translated and then rotated 90°.
e. Although Jasmine and Ilene were able to work together to rotate the points around the pivot point, now their lines are nowhere near the original lines. What transformation brings the system of equations back so that the pivot point returns to where it started and all other points have been rotated? Find the final image of the point (0,2).
Answer:
Applying the inverse translation that we did in part (c) brings the points back to where they should be. That is, for A’ = \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\), a point on the transformed system, add \(\left(\begin{array}{l}
x \\
y
\end{array}\right) + \left(\begin{array}{c}
3 \\
11
\end{array}\right)\). For \(\left(\begin{array}{l}
0 \\
2
\end{array}\right)\), we get
\(\left(\begin{array}{c}
9 \\
– 3
\end{array}\right) + \left(\begin{array}{c}
3 \\
11
\end{array}\right)\) = \(\left(\begin{array}{c}
12 \\
8
\end{array}\right)\)
f. Summarize your results in parts (a)–(e).
Answer:
To rotate a system of equations around its solution \(\left(\begin{array}{l}
a \\
b
\end{array}\right)\), we apply the following transformations to any arbitrary point \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\):
\(\left(\begin{array}{cc}
\cos (\theta) & – \sin (\theta) \\
\sin (\theta) & \cos (\theta)
\end{array}\right)\left(\left(\begin{array}{l}
x \\
y
\end{array}\right) – \left(\begin{array}{l}
a \\
b
\end{array}\right)\right)\) + \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\)
We translate the system so that the solution is mapped to the origin, then rotate the system, and then apply the inverse translation.
Extension:
Question 2.
Let b1 = \(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\) and b2 = \(\left(\begin{array}{l}
0 \\
1
\end{array}\right)\). Then answer the following:
a. Find 1 ⋅ b1 + 0 ⋅ b2.
Answer:
1 ⋅ \(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\) + 0 ⋅ \(\left(\begin{array}{l}
0 \\
1
\end{array}\right)\) = \(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\) + \(\left(\begin{array}{l}
0 \\
0
\end{array}\right)\) = \(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\) = b1
b. Find 0 ⋅ b1 + 1 ⋅ b2.
Answer:
0 ⋅ \(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\) + 1 ⋅ \(\left(\begin{array}{l}
0 \\
1
\end{array}\right)\) = \(\left(\begin{array}{l}
0 \\
0
\end{array}\right)\) + \(\left(\begin{array}{l}
0 \\
1
\end{array}\right)\) = \(\left(\begin{array}{l}
0 \\
1
\end{array}\right)\) = b2
c. Find 1 ⋅ b1 + 1 ⋅ b2.
Answer:
1 ⋅ \(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\) + 1 ⋅ \(\left(\begin{array}{l}
0 \\
1
\end{array}\right)\) = \(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\) + \(\left(\begin{array}{l}
0 \\
1
\end{array}\right)\) = \(\left(\begin{array}{l}
1 \\
1
\end{array}\right)\)
d. Find 3 ⋅ b1 + 2 ⋅ b2.
Answer:
3 ⋅ \(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\) + 2 ⋅ \(\left(\begin{array}{l}
0 \\
1
\end{array}\right)\) = \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) + \(\left(\begin{array}{l}
0 \\
2
\end{array}\right)\) = \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\)
e. Find 0 ⋅ b1 + 0 ⋅ b2.
Answer:
0 ⋅ \(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\) + 0 ⋅ \(\left(\begin{array}{l}
0 \\
1
\end{array}\right)\) = \(\left(\begin{array}{l}
0 \\
0
\end{array}\right)\) + \(\left(\begin{array}{l}
0 \\
0
\end{array}\right)\) = \(\left(\begin{array}{l}
0 \\
0
\end{array}\right)\)
f. Find x ⋅ b1 + y ⋅ b2 for x,y real numbers.
Answer:
x ⋅ \(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\) + y ⋅ \(\left(\begin{array}{l}
0 \\
1
\end{array}\right)\) = \(\left(\begin{array}{l}
x \\
0
\end{array}\right)\) + \(\left(\begin{array}{l}
0 \\
y
\end{array}\right)\) = \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\)
g. Summarize your results from parts (a)–(f). Can you use b1 and b2 to define any point in R2?
Answer:
In each case, the resultant vector was always equal to the scalar multiplied by the first vector for the
x – coordinate and the scalar multiplied by the second vector for the y – coordinate.
Question 3.
Let b1 = \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) and b2 = \(\left(\begin{array}{c}
– 2 \\
3
\end{array}\right)\). Then answer the following:
a. Find 1 ⋅ b1 + 1 ⋅ b2.
Answer:
1 ⋅ \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) + 1 ⋅ \(\left(\begin{array}{c}
– 2 \\
3
\end{array}\right)\) = \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) + \(\left(\begin{array}{c}
– 2 \\
3
\end{array}\right)\) = \(\left(\begin{array}{l}
1 \\
5
\end{array}\right)\)
b. Find 0 ⋅ b1 + 1 ⋅ b2.
Answer:
0 ⋅ \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) + 1 ⋅ \(\left(\begin{array}{c}
– 2 \\
3
\end{array}\right)\) = \(\left(\begin{array}{l}
0 \\
0
\end{array}\right)\) + \(\left(\begin{array}{c}
– 2 \\
3
\end{array}\right)\) = \(\left(\begin{array}{c}
– 2 \\
3
\end{array}\right)\) = b2
c. Find 1 ⋅ b1 + 0 ⋅ b2.
Answer:
1 ⋅ \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) + 0 ⋅ \(\left(\begin{array}{c}
– 2 \\
3
\end{array}\right)\) = \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) + \(\left(\begin{array}{l}
0 \\
0
\end{array}\right)\) = \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) = b1
d. Find – 4 ⋅ b1 + 2 ⋅ b2.
Answer:
– 4 ⋅ \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) + 2 ⋅ \(\left(\begin{array}{c}
– 2 \\
3
\end{array}\right)\) = \(\left(\begin{array}{c}
– 12 \\
– 8
\end{array}\right)\) + \(\left(\begin{array}{c}
– 4 \\
6
\end{array}\right)\) = \(\left(\begin{array}{c}
– 16 \\
– 2
\end{array}\right)\)
e. Solve r ⋅ b1 + s ⋅ b2 = 0.
Answer:
r ⋅ \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) + s ⋅ \(\left(\begin{array}{c}
– 2 \\
3
\end{array}\right)\) = \(\left(\begin{array}{l}
0 \\
0
\end{array}\right)\)
\(\left(\begin{array}{c}
3 r \\
2 r
\end{array}\right)\) + \(\left(\begin{array}{c}
– 2 s \\
3 s
\end{array}\right)\) = \(\left(\begin{array}{l}
0 \\
0
\end{array}\right)\)
\(\left(\begin{array}{l}
3 r – 2 s \\
2 r + 3 s
\end{array}\right)\) = \(\left(\begin{array}{l}
0 \\
0
\end{array}\right)\)
3r = 2s⇒r = \(\frac{2}{3}\) s
2(\(\frac{2}{3}\) s) + 3s = 0
\(\frac{4}{3}\) s + 3s = 0
4s + 9s = 0
13s = 0
s = 0
r = \(\frac{2}{3}\) ⋅ 0 = 0
So both r and s are zero.
f. Solve r ⋅ b1 + s ⋅ b2 = \(\left(\begin{array}{c}
22 \\
-7
\end{array}\right)\).
Answer:
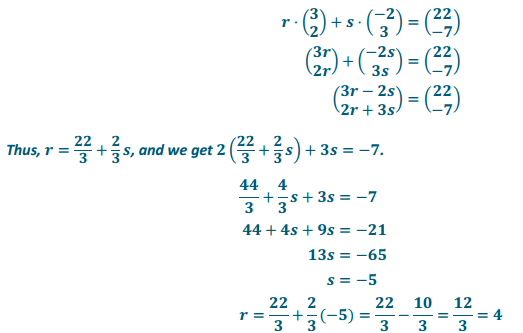
So, r = 4 and s = – 5.
g. Is there any point \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\) that cannot be expressed as a linear combination of b1 and b2 (i.e., where r ⋅ b1 + s ⋅ b2 = \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\) has real solutions, for x,y real numbers)?
Answer:
No. There was nothing special about the point \(\left(\begin{array}{l}
22 \\
– 7
\end{array}\right)\). We could have substituted in any other two values, performed the same steps, and arrived at a valid solution.
h. Explain your response to part (g) geometrically.
Answer:
Answers may vary. b1 and b2 are two vectors that intersect at the origin. They are not parallel, so through linear transformations, we can arrive at any point \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\). Alternatively, you can think of the equations
3r – 2s = x and 2r – 3s = y as lines in terms of r and s; then these lines are not parallel and thus are always consistent when used in a system of linear equations.
Eureka Math Precalculus Module 2 Lesson 24 Exit Ticket Answer Key
Question 1.
Consider the system of equations \(\left\{\begin{array}{c}
y = 5 x + 2 \\
y = 3 x
\end{array}\right.\), and perform the following operations on an arbitrary point \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\):
a. Rotate around the origin by θ.
Answer:
\(\left(\begin{array}{cc}
\cos (\theta) & – \sin (\theta) \\
\sin (\theta) & \cos (\theta)
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)\) = \(\left(\begin{array}{l}
x \cos (\theta) – y \sin (\theta) \\
x \sin (\theta) + y \cos (\theta)
\end{array}\right)\)
b. Translate by the opposite of the solution to the system.
Answer:
\(\left(\begin{array}{l}
x \\
y
\end{array}\right) – \left(\begin{array}{l}
– 1 \\
– 3
\end{array}\right)\) = \(\left(\begin{array}{l}
x + 1 \\
y + 3
\end{array}\right)\)
c. Apply a dilation of \(\frac{2}{3}\).
Answer:
\(\left(\begin{array}{ll}
\frac{2}{3} & 0 \\
0 & \frac{2}{3}
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)\) = \(\left(\begin{array}{l}
\frac{2}{3} x \\
\frac{2}{3} x
\end{array}\right)\)
Question 2.
What effect does each of the transformations in Problem 1 have on the solution of the system and on the origin?
Answer:
The solution of the system \(\left(\begin{array}{l}
– 1 \\
– 3
\end{array}\right)\) maps to \(\left(\begin{array}{l}
– \cos (\theta) + 3 \sin (\theta) \\
– \sin (\theta) – 3 \cos (\theta)
\end{array}\right),\left(\begin{array}{l}
0 \\
0
\end{array}\right)\), and \(\left(\begin{array}{r}
– \frac{2}{3} \\
– 2
\end{array}\right)\) respectively.
The origin maps to itself for the first and third transformations, which were linear transformations, and maps to the opposite of the system’s solution for the second transformation: \(\left(\begin{array}{l}
1 \\
3
\end{array}\right)\).