Eureka Math Precalculus Module 1 Lesson 9 Answer Key

Engage NY Eureka Math Precalculus Module 1 Lesson 9 Answer Key

Eureka Math Precalculus Module 1 Lesson 9 Example Answer Key

Example
Given the complex number z, find a complex number w such that z+w is shifted \(\sqrt{2}\) units in a southwest direction.

→ Begin by plotting the complex number. What does it mean for the point to be shifted in a southwest direction?
→ The point shifts to the left and down the same number of units.
→ A right triangle is formed. What are the values of the legs and the hypotenuse?
→ The legs are both x, and the hypotenuse is \(\sqrt{2}\).

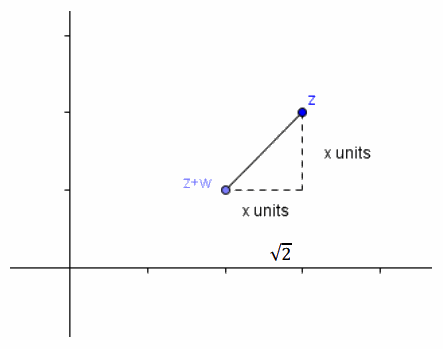
Give students an opportunity to solve for x on their own and use the information to determine the complex number w.
→ x²+x²=(\(\sqrt{2}\))²
→ 2x²=2, so x=1.
→ Since the point was shifted 1 unit down and 1 unit to the left, the complex number must be -1-i.

Eureka Math Precalculus Module 1 Lesson 9 Exercise Answer Key

Exercises

Exercise 1.
Taking the conjugate of a complex number corresponds to reflecting a complex number about the real axis. What operation on a complex number induces a reflection across the imaginary axis?
Answer:
For a complex number a+bi, the reflection across the imaginary axis is -a+bi. Alternatively, for a complex number z, the reflection across the imaginary axis is –\(\overline{\boldsymbol{z}}\).

Students may have answered that the reflection of a+bi across the imaginary axis is -a+bi. Discuss as a class how to write this in terms of the conjugate of the complex number.
→ Is it possible to write -a+bi another way? (Recall that the complex number z can be written as a+bi.)
→ Begin by factoring out -1: -1(a-bi).
→ Replace a-bi with \(\overline{\boldsymbol{z}}\): –\(\overline{\boldsymbol{z}}\).

Exercise 2.
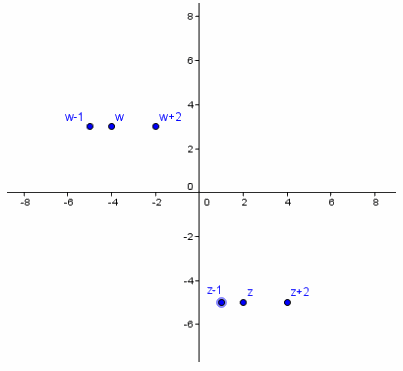
Given the complex numbers w=-4+3i and z=2-5i, graph each of the following:
a. w
b. z
c. w+2
d. z+2
e. w-1
f. z-1
Answer:

Exercise 3.
Describe in your own words the geometric effect adding or subtracting a real number has on a complex number.
Answer:
Adding a real number to a complex number shifts the point to the right on the real (horizontal) axis, while subtracting a real number shifts the point to the left.

When students have finished the exercise, confirm as a class the answer to Exercise 3.
→ Did your conjecture match the answer to Exercise 3?
→ Answers will vary.

Some students may no doubt have guessed that adding a positive real value (i.e., w+2) to the complex number would shift the point vertically instead of horizontally. They may be confusing the translation of a function, such as f(x)=x²,
with that of a complex number. Make clear that even though comparisons are made between the complex and coordinate planes, the geometric effects are different. Use the following discussion points to clarify.

→ What is the effect of adding a constant to a function like f(x)=x²? (For example, f(x)=x²+2.)
→ The graph of the parabola would shift upward 2 units.
→ How does this differ from adding the real number 2 to a complex number?
→ The point representing the complex number would shift two units to the right, not vertically like the function.

Exercise 4.
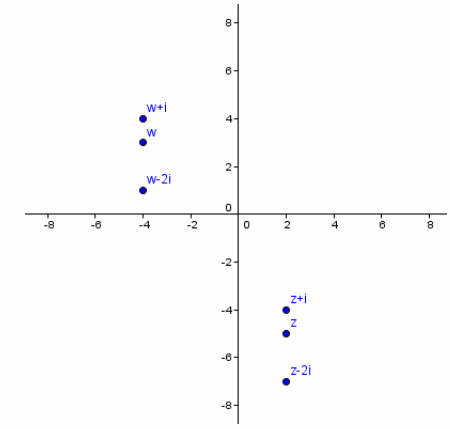
Given the complex numbers w=-4+3i and z=2-5i, graph each of the following:
a. w
b. z
c. w+i
d. z+i
e. w-2i
f. z-2i
Answer:

Exercise 5.
Describe in your own words the geometric effect adding or subtracting an imaginary number has on a complex number.
Answer:
Adding an imaginary number to a complex number shifts the point up the imaginary (vertical) axis, while subtracting an imaginary number shifts the point down.

Eureka Math Precalculus Module 1 Lesson 9 Problem Set Answer Key

Question 1.
Given the complex numbers w=2-3i and z=-3+2i, graph each of the following:

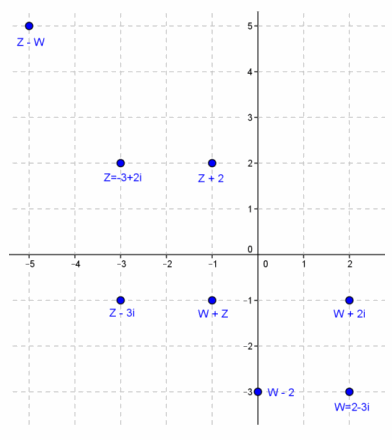
a. w-2
Answer:
w-2=2-3i-2=-3i

b. z+2
Answer:
z+2=-3+2i+2=-1+2i

c. w+2i
Answer:
w+2i=2-3i+2i=2-i

d. z-3i
Answer:
z-3i=-3+2i-3i=-3-i

e. w+z
Answer:
w+z=2-3i+(-3+2i)=-1-i

f. z-w
Answer:
z-w=-3+2i-(2-3i)=-5+5i

Question 2.
Let z=5-2i. Find w for each case.
a. z is a 90° counterclockwise rotation about the origin of w.
Answer:
w∙i=z; therefore, w=\(\frac{z}{i}\)=\(\frac{5-2 i}{i}\)=\(\frac{2+5 i}{-1}\)=-2-5i.

b. z is reflected about the imaginary axis from w.
Answer:
w=-\(\overline{\boldsymbol{z}}\); therefore, w=-(5+2i)=-5-2i.

c. z is reflected about the real axis from w.
Answer:
w=\(\overline{\boldsymbol{z}}\); therefore, w=5+2i.

Question 3.
Let z=-1+2i, w=4-i. Simplify the following expressions.

a. z+\(\overline{\boldsymbol{w}}\)
Answer:
z+\(\overline{\boldsymbol{w}}\)=-1+2i+4+i=3+3i

b. |w-\(\overline{\boldsymbol{z}}\) |
Answer:
|w-\(\overline{\boldsymbol{z}}\) |=|4-i-(-1-2i)|=|4-i+1+2i|=|5+i|=\(\sqrt{(5)^{2}+(1)^{2}}\)=\(\sqrt{26}\)

c. 2z-3w
Answer:
2z-3w=-2+4i-(12-3i)=-2+4i-12+3i=-14+7i

d. \(\frac{\boldsymbol{z}}{\boldsymbol{w}}\)
Answer:
\(\frac{\boldsymbol{z}}{\boldsymbol{w}}\)=\(\frac{-1+2 i}{4-i}\)=\(\frac{(-1+2 i)(4+i)}{(4-i)(4+i)}\)=\(\frac{-6+7 i}{16+1}\) = \(\frac{-6}{17}\) + \(\frac{7i}{17}\)

Question 4.
Given the complex number z, find a complex number w where z+w is shifted:
a. 2\(\sqrt{2}\) units in a northeast direction.
Answer:
x²+x²=(2\(\sqrt{2}\))², 2x²=8, x=±2. Therefore, w=2+2i.

b. 5\(\sqrt{2}\) units in a southeast direction.
Answer:
x²+x²=(5\(\sqrt{2}\))², 2x²=50, x=±5. Therefore, w=5-5i.

Eureka Math Precalculus Module 1 Lesson 9 Exit Ticket Answer Key

Question 1.
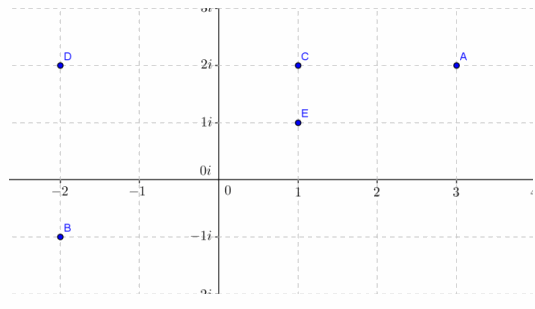
Given z=3+2i and w=-2-i, plot the following in the complex plane:
a. z
b. w
c. z-2
d. w+3i
e. w+z

Answer:

Question 2.
Given z=a+bi, what complex number represents the reflection of z about the imaginary axis? Give one example to show why.
Answer:
–\(\overline{\boldsymbol{z}}\), the negative conjugate of z. For example, z=2+3i,
–\(\overline{\boldsymbol{z}}\)=-(2-3i)=-2+3i, which is reflected about the imaginary axis.

Question 3.
What is the geometric effect of T(z)=z+(4-2i)?
Answer:
T(z) shifts 4 units to the right and the 2 units downward.