Eureka Math Precalculus Module 1 Lesson 2 Answer Key

Engage NY Eureka Math Precalculus Module 1 Lesson 2 Answer Key

Eureka Math Precalculus Module 1 Lesson 2 Exercise Answer Key

Exercise 1.
Let f(x) = sin(x). Does f(2x) = 2f(x) for all values of x? Is it true for any values of x? Show work to justify your answer.
Answer:
No. If x = \(\frac{\pi}{2}\), sin (2(\(\frac{\pi}{2}\))) = sin(π) = 0, but 2sin(\(\frac{\pi}{2}\)) = 2(1) = 2, so the statement does not hold for every value of x. It is true anytime sin(x) = 0., so for x = 0,
x = ±π, x = ±2π.

Exercise 2.
Let f(x) = log(x). Find a value for a such that (2a) = 2f(a). Is there one? Show work to justify your answer.
Answer:
log(2a) = 21og(a)
log(2a) = log(a²)
2a = a²
a² – 2a = 0
a(a – 2) = 0
Thus, a = 2 or a = 0. Because 0 is not in the domain of the logarithmic function, the only solution is a = 2.

Exercise 3.
Let f(x) = 10^x. Show that f(a + b) = f(a) + f(b) is true for a = b = log(2) and that it is not true for a = b = 2.
Answer:
For a = b = log(2)
f(a + b) = 1o^{(log(2)+log(2))} = 10^2log(2) = 10^log(22) = 2² = 4
f(a) + f(b) = 10^log2 + 10^log2 = 2 + 2 = 4
Therefore, f(a + b) = f(a) + f(b).
For a = b = 2
f(a + b) = 10²⁺² = 10⁴ = 10000
f(a) + f(b) = 10² + 10² = 100 + 100 = 200
Therefore, f(a + b) ≠ f(a) + f(b).

Exercise 4.
Let f(x) = \(\frac{1}{x}\). Are there any real numbers a and b so that f(a + b) = f(a) + f(b)? Explain.
Answer:
Neither a nor b can equal zero since they are in the denominator of the rational expressions.
\(\frac{1}{a+b}\) = \(\frac{1}{a}\) + \(\frac{1}{b}\)
\(\frac{1}{a+b}\)ab(a + b) = \(\frac{1}{a}\)ab(a + b) + \(\frac{1}{b}\)ab(a + b)
ab = a(a + b) + b(a + b)
ab = a² + ab + ab + b²
ab = a² + 2ab + b²
ab = (a + b)²
This means that ab must be a positive number. Simplifying further, we get 0 = a² + ab + b².
The sum of three positive numbers will never equal zero, so there are no real solutions for a and b.

Exercise 5.
What do your findings from these exercises illustrate about the linearity of these functions? Explain.
Answer:
Answers will vary but should address that in each case, the function is not a linear transformation because it does not hold to the conditions f(a + b) = f(a) + f(b) and f(cx) = c(f(x)) for all real-numbered inputs.

Eureka Math Precalculus Module 1 Lesson 2 Problem Set Answer Key

Assign students some or all of the functions to investigate. Problems 1-4 are all trigonometric functions, Problem 5 is a rational function, and Problems 6 and 7 are logarithmic functions. These can be divided up. Problem 8 sets up Lesson 3 but is quite challenging.

Examine the equations given in Problems 1-4, and show that the functions f(x) = cos(x) and g(x) = tan(x) are not linear transformations by demonstrating that they do not satisfy the conditions indicated for all real numbers. Then, find values of x and/or y for which the statement holds true.

Question 1.
cos(x + y) = cos(x) + cos(y)
Answer:
Answers that prove the statement false will vary but could include x = 0 and y = 0.
This statement is true when x = 1. 9455, or 111. 47°, and y = 1. 9455, or 111. 47°. This will be difficult for students to find without technology.

Question 2.
cos(2x) = 2cos(x)
Answer:
Answers that prove the statement false will vary but could include x = 0 or x = \(\frac{\pi}{2}\)
This statement is true when x = 1. 9455, or 111. 47°. This will be difficult for students to find without technology.
Answer:

Question 3.
tan(x + y) = tan(x) + tan(y)
Answer:
Answers that prove the statement false will vary but could include x = \(\frac{\pi}{4}\) and y = \(\frac{\pi}{4}\).
This statement is true when x = 0 and y = 0.

Question 4.
tan(2x) = 2tan(x)
Answer:
Answers that prove the statement false will vary but could include x = \(\frac{\pi}{4}\) and y = \(\frac{\pi}{4}\).
This statement is true when x = 0 and y = 0.

Question 5.
Let f(x) = \(\frac{1}{x^{2}}\). Are there any real numbers a and b so that f(a + b) = f(a) + f(b)? Explain.
Answer:
Neither a nor b can equal zero since they are in the denominator of the fractions.
If f(a + b) = f(a) + f(b), then \(\frac{1}{(a+b)^{2}}\) = \(\frac{1}{a^{2}}\) + \(\frac{1}{b^{2}}\).
Multiplying each term by a²b²(a + b)², we get
a²b²(a + b)²\(\frac{1}{(a+b)^{2}}\)= a²b²(a + b)²\(\frac{1}{a^{2}}\)+ a²b²(a + b)²\(\frac{1}{b^{2}}\)
a²b² = b²(a + b)² + a²(a + b)²
a²b² = (a² + b²)(a + b)²
a²b² = a⁴ + 2a³b + 2a²b² + 2ab³ + b⁴
a²b² = a⁴ + 2ab(a² + b²) + 2a²b² + b⁴
0 = a⁴ + 2ab(a² + b²) + a²b² + b⁴
The terms a⁴, a²b², and b⁴ are positive because they are even-numbered powers of nonzero numbers. We established in the lesson that ab = (a + b)² and, therefore, is also positive.
The product 2ab(a² + b²) must then also be positive.
The sum of four positive numbers will never equal zero, so there are no real solutions for a and b.

Question 6.
Let f(x) = log(x). Find values of a such that f(3a) = 3f(a).
Answer:
log(3a) = 31og(a)
log(3a) = log(a)³
3a = a³
3 = a²
a = \(\sqrt{3}\)
This is true for the value of a when 3a = a³ that is in the domain, which is a = \(\sqrt{3}\).

Question 7.
Let f(x) = log(x). Find values of a such that f(ka) = kf(a).
Answer:
This is true for the values of a when ka = ak that are in the domain of the function.

Question 8.
Based on your results from the previous two problems, form a conjecture about whether f(x) = log(x) represents a linear transformation.
Answer:
The function is not an example of a linear transformation. The condition f(ka) = kf(a) does not hold for all values of a, for example, nonzero values of c and a = 1.

Question 9.
Let f(x) = ax² + bx + c.
a. Describe the set of all values for a, b, and c that make f(x + y)= f(x) + f(y) valid for all real numbers x and y.
Answer:
This is challenging for students, but the goal is for them to realize that a = 0, c = 0, and any real number b. They may understand that a = 0, but c = 0 could be more challenging. The point is that it is unusual for functions to satisfy this condition for all real values of x and y. This is discussed in detail in Lesson 3.
f(x + y) = a(x + y)² + b(x + y) + c = ax² + 2axy + ay² + bx + by + c
f(x) + f(y) = ax² + bx + c + ay² + by + c
f(x + y)= f(x) + f(y)
ax² + 2axy + ay² + bx + by + c = ax² + bx + c + ay² + by + c
2axy + c = c + c
2axy = c
Therefore, the set of values that satisfies this equation for all real numbers x and y is a = 0, any real number b, and c = 0.

b. What does your result indicate about the linearity of quadratic functions?
Answer:
Answers will vary but should address that quadratic functions are not linear transformations, since they only meet the condition f(x + y) = f(x) + f(y) when a = 0.

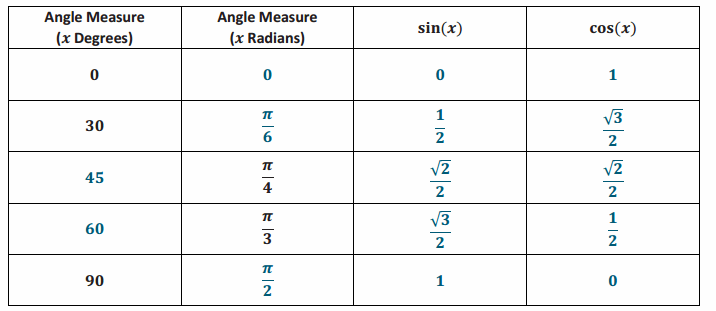
Trigonometry Table

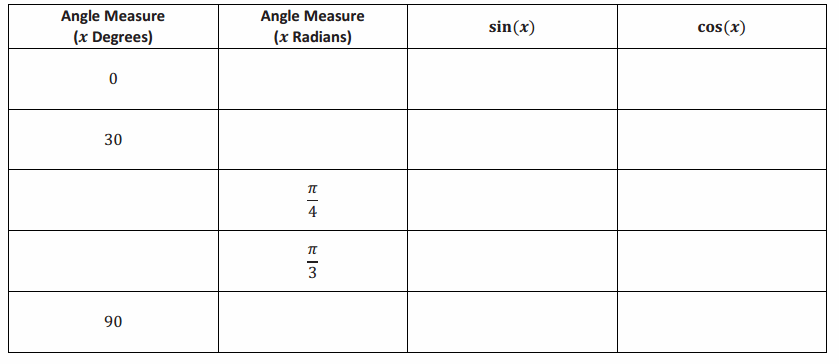
Answer:

Eureka Math Precalculus Module 1 Lesson 2 Exit Ticket Answer Key

Question 1.
Koshi says that he knows that sin(x + y) = sin(x) + sin(y) because he has substituted in multiple values for x and y, and they all work. He has tried x = 0° and y = 0°, but he says that usually works, so he also tried x = 45° and y = 180°, x = 90° and y = 270°, and several others. Is Koshi correct? Explain your answer.
Answer:
Koshi is not correct. He happened to pick values that worked, most giving at least one value of sin(x) = 0. If he had chosen other values such as x = 30° and y = 60°, sin(30° + 60°) = sin(90°) = 1, but sin(30°) + sin(60°) = \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\), so the statement that sin(30° + 60°) = sin(30°) + sin(60°) is false.

Question 2.
Is f(x) = sin(x) a linear transformation? Why or why not?
Answer:
No. sin(x + y) ≠ sin(x) + sin(y) and sin(ax) ≠ a sin(x)