Engage NY Eureka Math 8th Grade Module 4 Lesson 9 Answer Key
Eureka Math Grade 8 Module 4 Lesson 9 Exercise Answer Key
Exercise 1.
Write the equation for the 15th step.
Answer:
S15-7+7∙515=5S15
Exercise 2.
How many people would see the photo after 15 steps? Use a calculator if needed.
Answer:
S15-7+7∙515=5S15
S15-5S15-7++7∙515=5S15-5S15
S15 (1-5)-7+7∙515=0
S15 (1-5)-7+7+7∙515-7∙515=7-7∙515
S15 (1-5)=7(1-515 )
S15=\(\frac{7\left(1-5^{15}\right)}{(1-5)}\)
S15=53 405 761 717
Exercises 3–11 as an Alternative to Discussion
Students should be able to complete the following problems independently as they are an application of skills learned to this point, namely, transcription and solving linear equations in one variable. Have students work on the problems one at a time and share their work with the whole class, or assign the entire set and allow students to work at their own pace. Provide correct solutions at the end of the lesson.
Exercise 3.
Marvin paid an entrance fee of $5 plus an additional $1.25 per game at a local arcade. Altogether, he spent $26.25. Write and solve an equation to determine how many games Marvin played.
Let x represent the number of games he played.
5+1.25x=26.25
1.25x=21.25
x=\(\frac{21.25}{1.25}\)
x=17
Marvin played 17 games.
Exercise 4.
The sum of four consecutive integers is -26. What are the integers?
Answer:
Let x be the first integer.
x+(x+1)+(x+2)+(x+3)=-26
4x+6=-26
4x=-32
x=-8
The integers are -8, -7, -6, and -5.
Exercise 5.
A book has x pages. How many pages are in the book if Maria read 45 pages of a book on Monday, \(\frac{1}{2}\) the book on Tuesday, and the remaining 72 pages on Wednesday?
Answer:
Let x be the number of pages in the book.
x=45+\(\frac{1}{2}\) x+72
x=117+\(\frac{1}{2}\) x
\(\frac{1}{2}\) x=117
x=234
The book has 234 pages.
Exercise 6.
A number increased by 5 and divided by 2 is equal to 75. What is the number?
Answer:
Let x be the number.
\(\frac{x+5}{2}\)=75
x+5=150
x=145
The number is 145.
Exercise 7.
The sum of thirteen and twice a number is seven less than six times a number. What is the number?
Answer:
Let x be the number.
13+2x=6x-7
20+2x=6x
20=4x
5=x
The number is 5.
Exercise 8.
The width of a rectangle is 7 less than twice the length. If the perimeter of the rectangle is 43.6 inches, what is the area of the rectangle?
Answer:
Let x represent the length of the rectangle.
2x+2(2x-7)=43.6
2x+4x-14=43.6
6x-14=43.6
6x=57.6
x=\(\frac{57.6}{6}\)
x=9.6
The length of the rectangle is 9.6 inches, and the width is 12.2 inches, so the area is 117.12 in2.
Exercise 9.
Two hundred and fifty tickets for the school dance were sold. On Monday, 35 tickets were sold. An equal number of tickets were sold each day for the next five days. How many tickets were sold on one of those days?
Answer:
Let x be the number of tickets sold on one of those days.
250=35+5x
215=5x
43=x
43 tickets were sold on each of the five days.
Exercise 10.
Shonna skateboarded for some number of minutes on Monday. On Tuesday, she skateboarded for twice as many minutes as she did on Monday, and on Wednesday, she skateboarded for half the sum of minutes from Monday and Tuesday. Altogether, she skateboarded for a total of three hours. How many minutes did she skateboard each day?
Answer:
Let x be the number of minutes she skateboarded on Monday.
x+2x+\(\frac{2 x+x}{2}\)=180
\(\frac{2 x}{2}\)+\(\frac{4 x}{2}\)+\(\frac{2 x+x}{2}\)=180
\(\frac{9 x}{2}\)=180
9x=360
x=40
Shonna skateboarded 40 minutes on Monday, 80 minutes on Tuesday, and 60 minutes on Wednesday.
Exercise 11.
In the diagram below, △ABC ~△A^’ B^’ C^’. Determine the length of \(\overline{A C}\) and \(\overline{B C}\).
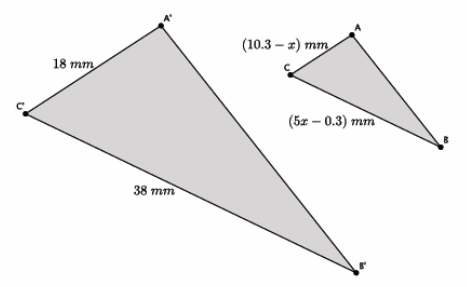
Answer:
\(\frac{18}{10.3-x}\)=\(\frac{38}{5 x-0.3}\)
18(5x-0.3)=38(10.3-x)
90x-5.4=391.4-38x
128x-5.4=391.4
128x=396.8
x=\(\frac{396.8}{128}\)
x=3.1
The length of \(\overline{A C}\) is 7.2 mm, and the length of \(\overline{B C}\) is 15.2 mm.
Eureka Math Grade 8 Module 4 Lesson 9 Exit Ticket Answer Key
Question 1.
Rewrite the equation that would represent the sum in the fifth step of the Facebook problem:
S5=7+7∙5+7∙52+7∙53+7∙54
S5=7+7∙5+7∙52+7∙53+7∙54
S5-7=7∙5+7∙52+7∙53+7∙54
S5-7+7∙55=7∙5+7∙52+7∙53+7∙54+7∙55
S5-7+7∙55=5(7+7∙5+7∙52+7∙53+7∙54 )
S5-7+7∙55=5(S5 )
S5-5S5-7+7∙55=0
S5-5S5=7-(7∙55 )
(1-5) S5=7-(7∙55 )
(1-5) S5=7(1-55 )
S5=\(\frac{7\left(1-5^{5}\right)}{1-5}\)
Question 2.
The sum of four consecutive integers is 74. Write an equation, and solve to find the numbers.
Answer:
Let x be the first number.
x+(x+1)+(x+2)+(x+3)=74
4x+6=74
4x=68
x=17
The numbers are 17, 18, 19, and 20.
Eureka Math Grade 8 Module 4 Lesson 9 Problem Set Answer Key
Assign the problems that relate to the elements of the lesson that were used with students.
Question 1.
You forward an e-card that you found online to three of your friends. They liked it so much that they forwarded it on to four of their friends, who then forwarded it on to four of their friends, and so on. The number of people who saw the e-card is shown below. Let S5 represent the number of people who saw the e-card after one step, let S2 represent the number of people who saw the e-card after two steps, and so on.
S5=3
S2=3+3∙4
S3=3+3∙4+3∙42
S4=3+3∙4+3∙42+3∙43
a. Find the pattern in the equations.
Answer:
S2=3+3∙4
S2-3=3∙4
S2-3+3∙42=3∙4+3∙42
S2-3+3∙42=4(3+3∙4)
S2-3+3∙42=4S2
S3=3+3∙4+3∙42
S3-3=3∙4+3∙42
S3-3+3∙43=3∙4+3∙42+3∙43
S3-3+3∙43=4(3+3∙4+3∙42 )
S3-3+3∙43=4S3
S4=3+3∙4+3∙42+3∙43
S4-3=3∙4+3∙42+3∙43
S4-3+3∙44=3∙4+3∙42+3∙43+3∙44
S4-3+3∙44=4(3+3∙4+3∙42+3∙43 )
S4-3+3∙44=4S4
b. Assuming the trend continues, how many people will have seen the e-card after 10 steps?
Answer:
S50-3+3∙410=4S10
S10-4S10-3+3∙410=0
S10(1-4)=3-3∙410
S10(1-4)=3(1-410)
S10=\(\frac{3\left(1-4^{10}\right)}{(1-4)}\)
S10=1 048 575
After 10 steps, 1,048,575 people will have seen the e-card.
c. How many people will have seen the e-card after n steps?
Answer:
Sn=\(\frac{3\left(1-4^{n}\right)}{(1-4)}\)
For each of the following questions, write an equation, and solve to find each answer.
Question 2.
Lisa has a certain amount of money. She spent $39 and has \(\frac{3}{4}\) of the original amount left. How much money did she have originally?
Answer:
Let x be the amount of money Lisa had originally.
x-39=\(\frac{3}{4}\) x
-39=-\(\frac{1}{4}\) x
156=x
Lisa had $156 originally.
Question 3.
The length of a rectangle is 4 more than 3 times the width. If the perimeter of the rectangle is 18.4 cm, what is the area of the rectangle?
Answer:
Let x represent the width of the rectangle.
2(4+3x)+2x=18.4
8+6x+2x=18.4
8+8x=18.4
8x=10.4
x=\(\frac{10.4}{8}\)
x=1.3
The width of the rectangle is 1.3 cm, and the length is 7.9 cm, so the area is 10.27 cm2.
Question 4.
Eight times the result of subtracting 3 from a number is equal to the number increased by 25. What is the number?
Answer:
Let x be the number.
8(x-3)=x+25
8x-24=x+25
7x-24=25
7x=49
x=7
The number is 7.
Question 5.
Three consecutive odd integers have a sum of 3. What are the numbers?
Answer:
Let x be the first odd number.
x+(x+2)+(x+4)=3
3x+6=3
3x=-3
x=-1
The three consecutive odd integers are -1, 1, and 3.
Question 6.
Each month, Liz pays $35 to her phone company just to use the phone. Each text she sends costs her an additional $0.05. In March, her phone bill was $72.60. In April, her phone bill was $65.85. How many texts did she send each month?
Answer:
Let x be the number of texts she sent in March.
35+0.05x=72.60
0.05x=37.6
x=\(\frac{37.6}{0.05}\)
x=752
She sent 752 texts in March.
Let y be the number of texts she sent in April.
35+0.05y=65.85
0.05y=30.85
y=\(\frac{30.85}{0.05}\)
y=617
She sent 617 texts in April.
Question 7.
Claudia is reading a book that has 360 pages. She read some of the book last week. She plans to read 46 pages today. When she does, she will be \(\frac{4}{5}\) of the way through the book. How many pages did she read last week?
Answer:
Let x be the number of pages she read last week.
x+46=\(\frac{4}{5}\) (360)
x+46=288
x=242
Claudia read 242 pages last week.
Question 8.
In the diagram below, △ABC ~△A^’ B^’ C^’. Determine the measure of ∠A.
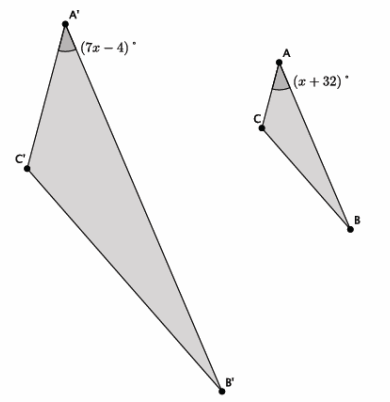
Answer:
7x-4=x+32
6x-4=32
6x=36
x=6
The measure of ∠A is 38°.
Question 9.
In the diagram below, △ABC ~△A^’ B^’ C^’. Determine the measure of ∠A.
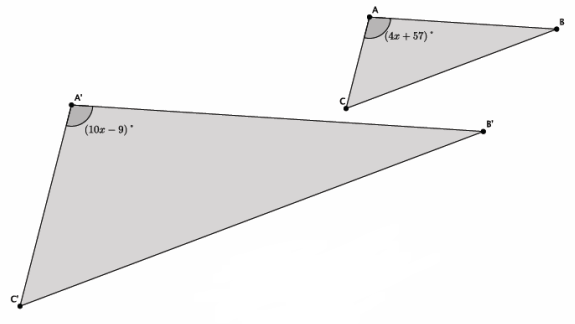
Answer:
10x-9=4x+57
6x-9=57
6x=66
x=11
The measure of ∠A is 101°.