Engage NY Eureka Math 8th Grade Module 4 End of Module Assessment Answer Key
Eureka Math Grade 8 Module 4 End of Module Assessment Task Answer Key
Question 1.
Use the graph below to answer parts (a)–(c).
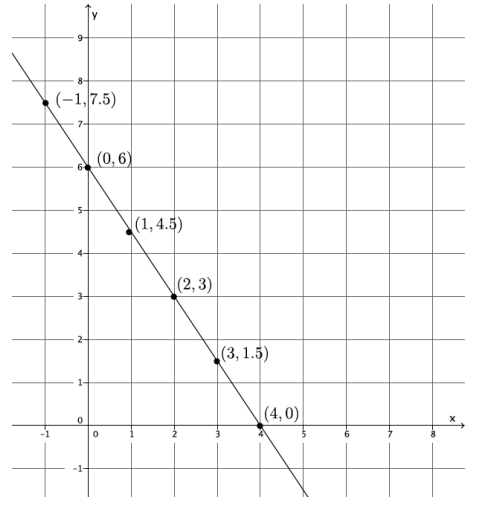
a. Use any pair of points to calculate the slope of the line.
Answer:
m = \(\frac{6-3}{0-2}=\frac{3}{-2}\) = –\(\frac{3}{2}\)
b. Use a different pair of points to calculate the slope of the line.
Answer:
m = \(\frac{6-0}{0-4}=\frac{6}{-4}\) = –\(\frac{3}{2}\)
c. Explain why the slopes you calculated in parts (a) and (b) are equal.
Answer:
The slopes are equal because the slope triangle are similar, ∆ABC ~ ∆AB’C’. Each triangle has 90° angle at ∠ABC & ∠AB’C’, respectively. They are 90° because they are at intersection of the grid lines. Both triangles share ∠BAC. By the AA criterion ∆ABC ~ ∆AB’C’, which means their corresponding sides are equal in ratio.
\(\frac{\left|B^{\prime} C^{\prime}\right|}{|B C|}=\frac{\left|A B^{\prime}\right|}{|A B|}\) which is the same as \(\frac{\left|B^{\prime} C^{\prime}\right|}{\left|A B^{\prime}\right|}=\frac{|B C|}{|A B|}\) where –\(\frac{\left|B^{\prime} C^{\prime}\right|}{\left|A B^{\prime}\right|}\) is the slope in (b) and –\(\frac{|B C|}{|A B|}\) is the slope in (a).
Question 2.
Jeremy rides his bike at a rate of 12 miles per hour. Below is a table that represents the number of hours and miles Kevin rides. Assume both bikers ride at a constant rate.
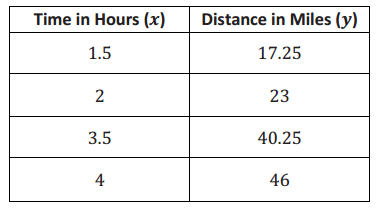
a. Which biker rides at a greater speed? Explain your reasoning.
Answer:
Let Y be the distance triangled and X be the number of hours,
Then for jeremy, \(\frac{y}{x}\) = \(\frac{12}{1}\) ⇒ 12x
For kevin, \(\frac{46-23}{4-2}\) = \(\frac{23}{2}\) = 11.5, then y = 11.5x
When you compare their rates, 12 > 11.5, therefore jeremy rides at a greater speed.
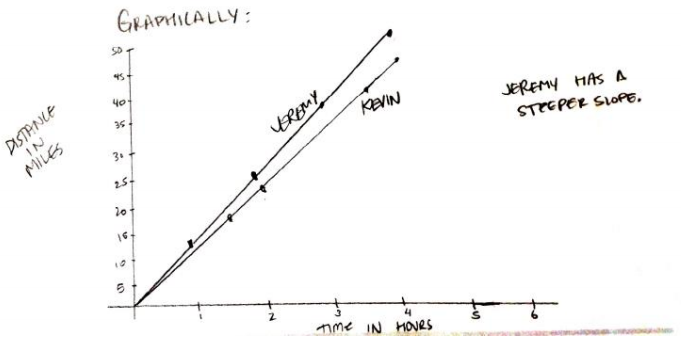
Graphically:
b. Write an equation for a third biker, Lauren, who rides twice as fast as Kevin. Use y to represent the number of miles Lauren travels in x hours. Explain your reasoning.
Answer:
“Twice as Fast” means lauren goes twice the distance in the same time. Then in 2 hours she rides 46 miles and in 4 hours, 92 miles. If y is the total distance in x hours, y = \(\frac{46}{2}\) x
y = 23x
c. Create a graph of the equation in part (b).
Answer:
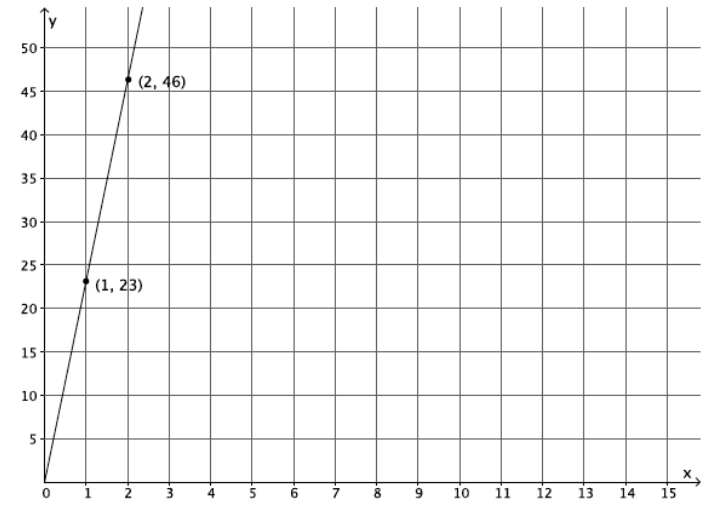
d. Calculate the slope of the line in part (c), and interpret its meaning in this situation.
Answer:
m = \(\frac{46-23}{2-1}\) = \(\frac{23}{1}\)
The slope is the rate that lauren rides, 23 miles per hour.
Question 3.
The cost of five protractors is $14.95 at Store A. The graph below compares the cost of protractors at Store A with the cost at Store B.
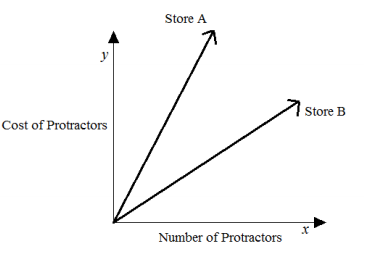
Estimate the cost of one protractor at Store B. Use evidence from the graph to justify your answer.
Answer:
The cost of protractors at store B is probably about $2.99 per protractor and it looks like the slope for store B is about half of the slope for store A.

Question 4.
Given the equation 3x+9y=-8, write a second linear equation to create a system that:
a. Has exactly one solution. Explain your reasoning.
Answer:
4x + 9y = -10
This equation has a slope different from 3x + 9y = -8. So the graphs of the equations will intersect.
b. Has no solution. Explain your reasoning.
Answer:
x + 3y = 10
This equation has the same slopes as 3x + 9y = -8, And no common points (solutions) Therefore the graphs of the equation are parallel lines.
c. Has infinitely many solutions. Explain your reasoning.
Answer:
6x + 18y = -16
This equation defines the same line as 3x + 9y = -8 and the graphs of the equations will coincide.
d. Interpret the meaning of the solution, if it exists, in the context of the graph of the following system of equations.
-5x+2y=10
10x-4y=-20
Answer:
-5x+2y=10 m = \(\frac{5}{2}\) (0, 5)
10x-4y=-20 m = \(\frac{5}{2}\) (0, 5)
This system will have infinitely many solutions because the graphs of these linear equations are the same line. Each equation has a slope of m = \(\frac{5}{2}\) and a y-intercept at (0, 5). There exists only one line through a point and a given slope. Therefore this system graphs as the same line and has infinitely many solutions.
Question 5.
Students sold 275 tickets for a fundraiser at school. Some tickets are for children and cost $3, while the rest are adult tickets that cost $5. If the total value of all tickets sold was $1,025, how many of each type of ticket was sold?
Answer:
Let X be the # of kids tickets
Let Y be the # of adults tickets
x + y = 275
3x + 5y = 1025
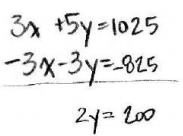
y = 100
x + 100 = 275
x = 175
(175, 100)
175 children’s tickets and 100 adults tickets were sold.
Question 6.
a. Determine the equation of the line connecting the points (0,-1) and (2,3).
Answer:
m = \(\frac{3-(-1)}{2 – 0}\) = \(\frac{4}{2}\) = 2
y = 2x – 1
b. Will the line described by the equation in part (a) intersect the line passing through the points (-2,4) and (-3,3)? Explain why or why not.
Answer:
m = \(\frac{4-3}{-2-(3)}\) = \(\frac{1}{1}\)
Yes, The lines will intersect because they have different slopes they will eventually intersect.
Question 7.
Line l1 and line l2 are shown on the graph below. Use the graph to answer parts (a)–(f).
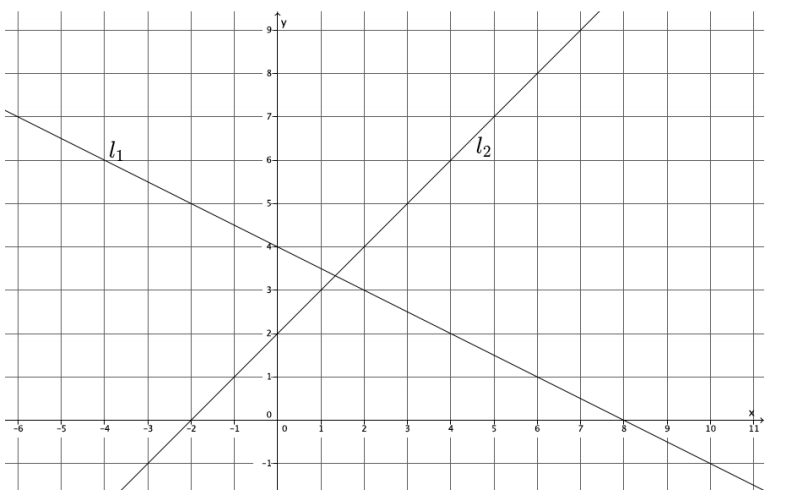
a. What is the y-intercept of l1?
Answer:
(0, 4)
b. What is the y-intercept of l2?
Answer:
(0, 2)
c. Write a system of linear equations representing lines l1 and l2.
Answer:
l1 : y = \(\frac{1}{2}\)x + 4
l2 : y = x + 2
d. Use the graph to estimate the solution to the system.
Answer:
(1.2, 3.3)
e. Solve the system of linear equations algebraically.
Answer:
y = \(\frac{1}{2}\)x + 4
y = x + 2
–\(\frac{1}{2}\) x + 4 = x + 2
4 = \(\frac{3}{2}\) x + 2
2 = \(\frac{3}{2}\) x
\(\frac{4}{3}\) = x
y = \(\frac{4}{3}\) + 2
= \(\frac{10}{3}\)
(\(\frac{4}{3}\), \(\frac{10}{3}\))
f. Show that your solution from part (e) satisfies both equations.
Answer:
\(\frac{10}{3}\) = –\(\frac{1}{2}\)(\(\frac{4}{3}\)) + 4
\(\frac{10}{3}\) = –\(\frac{2}{3}\) + 4
\(\frac{10}{3}\) = \(\frac{10}{3}\)
\(\frac{10}{3}\) = \(\frac{4}{3}\) + 2
\(\frac{10}{3}\) = \(\frac{10}{3}\)