Engage NY Eureka Math 7th Grade Module 4 Lesson 7 Answer Key
Eureka Math Grade 7 Module 4 Lesson 7 Example Answer Key
Example 1: A Video Game Markup
Games Galore Super Store buys the latest video game at a wholesale price of $30.00. The markup rate at Game’s Galore Super Store is 40%. You use your allowance to purchase the game at the store. How much will you pay, not including tax?
a. Write an equation to find the price of the game at Games Galore Super Store. Explain your equation.
Answer:
Let P represent the price of the video game.
Quantity = Percent × Whole
P = (100% + 40%)(30)
The equation shows that the price of the game at the store is equal to the wholesale cost, which is 100% and the 40% increase. This makes the new price 140% of the wholesale price.
b. Solve the equation from part (a).
Answer:
P = (100% + 40%)(30)
P = (1.40)(30)
P = 42
I would pay $42.00 if I bought it from Games Galore Super Store.
c. What was the total markup of the video game? Explain.
Answer:
The markup was $12.00 because $42 – $30 = $12.
d. You and a friend are discussing markup rate. He says that an easier way to find the total markup is by multiplying the wholesale price of $30.00 by 40%. Do you agree with him? Why or why not?
Answer:
Yes, I agree with him because (0.40)(30) = 12. The markup rate is a percent of the wholesale price. Therefore, it makes sense to multiply them together because Quantity = Percent × Whole.
→ Which quantity is the whole quantity in this problem?
The wholesale price is the whole quantity.
→ How do 140% and 1.4 correspond in this situation?
The markup price of the video game is 140% times the wholesale price. 140% and 1.4 are equivalent forms of the same number. In order to find the markup price, convert the percent to a decimal or fraction, and multiply it by the whole.
→ What does a markup mean?
A markup is the amount of increase in a price.
Example 2: Black Friday
A $300 mountain bike is discounted by 30% and then discounted an additional 10% for shoppers who arrive before
5:00 a.m.
a. Find the sales price of the bicycle.
Answer:
Find the price with the 30% discount:
Let D represent the discount price of the bicycle with the 30% discount rate.
Quantity = Percent × Whole
D = (100% – 30%)(300)
D = (0.70)(300)
D = 210
$210 is the discount price of the bicycle with the 30% discount rate.
Find the price with the additional 10% discount:
Let A represent the discount price of the bicycle with the additional 10% discount.
A = (100% – 10%)(210)
D = (1 – 0.10)(210)
D = (0.90)(210)
D = 189
$189 is the discount price of the bicycle with the additional 10% discount.
b. In all, by how much has the bicycle been discounted in dollars? Explain.
Answer:
$300 – $189 = $111. The bicycle has been discounted $111 because the original price was $300. With both discounts applied, the new price is $189.
c. After both discounts were taken, what was the total percent discount?
Answer:
A final discount of 40% means that you would add 30% to 10% and apply it to the same whole. This is not the case because the additional 10% discount is taken after the 30% discount has been applied, so you are only receiving that 10% discount on 70% of the original price. A 40% discount would make the final price $180 because 180 = (0.60)(300).
However, the actual final discount as a percent is 37%.
Let P be the percent the sales price is of the original price. Let F represent the actual final discount as a percent.
Part = Percent × Whole
189 = P × 300
(\(\frac{1}{300}\))189 = P × 300(\(\frac{1}{300}\))
0.63 = 63% = P
F = 100% – 63% = 37%
d. Instead of purchasing the bike for $300, how much would you save if you bought it before 5:00 a.m.?
Answer:
You would save $111 if you bought the bike before 5:00 a.m. because $300 – $189 is $111.
Example 3: Working Backward
A car that normally sells for $20,000 is on sale for $16,000. The sales tax is 7.5%.
→ What is the whole quantity in this problem?
a. The whole quantity is the original price of the car, $20,000.
Answer:
What percent of the original price of the car is the final price?
Quantity = Percent × Whole
16,000 = P(20,000)
16,000(\(\frac{1}{20,000}\)) = P(20,000)(\(\frac{1}{20,000}\))
0.8 = P
0.8 = \(\frac{80}{100}\) = 80%
The final price is 80% of the original price.
b. Find the discount rate.
Answer:
The discount rate is 20% because 100% – 80% = 20%.
c. By law, sales tax has to be applied to the discount price. However, would it be better for the consumer if the 7.5% sales tax was calculated before the 20% discount was applied? Why or why not?
Answer:
Apply Sales Tax First
Apply the sales tax to the whole.
(100% + 7.5%)(20,000)
(1 + 0.075)(20,000)
(1.075)(20,000)
$21,500 is the price of the car, including tax, before the discount.
Apply the discount to the new whole.
(100% – 20%)(21,500)
(1 – 0.2)(21,500)
$17,200 is the final price, including the discount and tax.
Apply the Discount First
(100% + 7.5%)(16,000)
(1 + 0.075)(16,000)
(1.075)(16,000)
$17,200 is the final price, including the discount and tax.
Because both final prices are the same, it does not matter which is applied first. This is because multiplication is commutative. The discount rate and sales tax rate are both being applied to the whole, $20,000.
d. Write an equation applying the commutative property to support your answer to part (c).
Answer:
20,000(1.075)(0.8) = 20,000(0.8)(1.075)
Eureka Math Grade 7 Module 4 Lesson 7 Exercise Answer Key
Exercises 1–3
Exercise 1.
Sasha went shopping and decided to purchase a set of bracelets for 25% off the regular price. If Sasha buys the bracelets today, she will save an additional 5%. Find the sales price of the set of bracelets with both discounts. How much money will Sasha save if she buys the bracelets today?

Answer:
Let B be the sales price with both discounts in dollars.
B = (0.95)(0.75)(44) = 31.35. The sales price of the set of bracelets with both discounts is $31.35. Sasha will save $12.65.
Exercise 2.
A golf store purchases a set of clubs at a wholesale price of $250. Mr. Edmond learned that the clubs were marked up 200%. Is it possible to have a percent increase greater than 100%? What is the retail price of the clubs?
Answer:
Yes, it is possible. Let C represent the retail price of the clubs, in dollars.
C = (100% + 200%)(250)
C = (1 + 2)(250)
C = (3)(250)
C = 750
The retail price of the clubs is $750.
Exercise 3.
Is a percent increase of a set of golf clubs from $250 to $750 the same as a markup rate of 200%? Explain.
Answer:
Yes, it is the same. In both cases, the percent increase and markup rate show by how much (in terms of percent) the new price is over the original price. The whole is $250 and corresponds to 100%. \(\frac{750}{250}\) = \(\frac{3}{1}\) × 100% = 300%. $750 is 300% of $250. 300% – 100% = 200%. From Exercise 2, the markup is 200%. So, percent increase is the same as markup.
Exercise 4.
a. Write an equation to determine the selling price in dollars, p, on an item that is originally priced s dollars after a markup of 25%.
Answer:
p = 1.25s or p = (0.25 + 1)s
b. Create and label a table showing five possible pairs of solutions to the equation.
Answer:
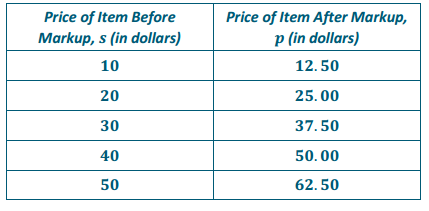
c. Create and label a graph of the equation.
Answer:
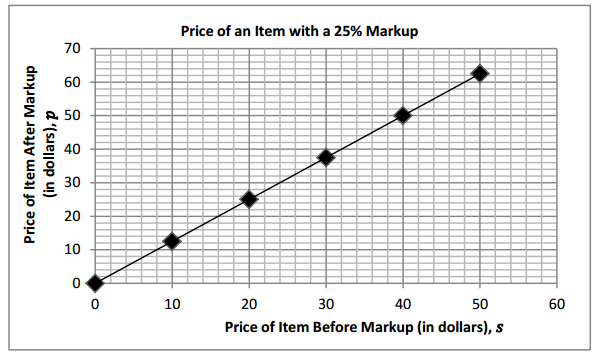
d. Interpret the points (0, 0) and (1, r).
Answer:
The point (0, 0) means that a $0 (free) item will cost $0 because the 25% markup is also $0. The point (1, r) is (1, 1.25). It means that a $1.00 item will cost $1.25 after it is marked up by 25%; r is the unit rate.
Exercise 5.
Use the following table to calculate the markup or markdown rate. Show your work. Is the relationship between the original price and the selling price proportional or not? Explain.
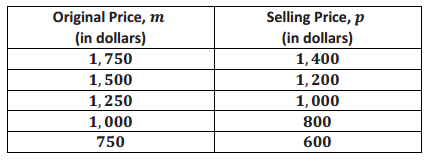
Answer:
Because the selling price is less than the original price, use the equation: Selling Price = (1 – m) × Whole.
1,400 = (1 – m)(1,750)
\(\frac{1,400}{1,750}\) = (1 – m)\(\frac{1,750}{1,750}\)
0.80 = 1 – m
0.20 = m
The markdown rate is 20%. The relationship between the original price and selling price is proportional because the table shows the ratio \(\frac{p}{m}\) = \(\frac{0.80}{1}\) for all possible pairs of solutions.
Eureka Math Grade 7 Module 4 Lesson 7 Problem Set Answer Key
Question 1.
You have a coupon for an additional 25% off the price of any sale item at a store. The store has put a robotics kit on sale for 15% off the original price of $40. What is the price of the robotics kit after both discounts?
Answer:
(0.75)(0.85)(40) = 25.50. The price of the robotics kit after both discounts is $25.50.
Question 2.
A sign says that the price marked on all music equipment is 30% off the original price. You buy an electric guitar for the sale price of $315.
a. What is the original price?
Answer:
\(\frac{315}{1 – 0.30}\) = \(\frac{315}{0.70}\) = 450. The original price is $450.
b. How much money did you save off the original price of the guitar?
Answer:
450 – 315 = 135. I saved $135 off the original price of the guitar.
c. What percent of the original price is the sale price?
Answer:
\(\frac{315}{450}\) = \(\frac{70}{100}\) = 70%. The sale price is 70% of the original price.
Question 3.
The cost of a New York Yankee baseball cap is $24.00. The local sporting goods store sells it for $30.00. Find the markup rate.
Answer:
Let P represent the unknown percent.
30 = P(24)
P = \(\frac{30}{24}\) = 1.25 = (100% + 25%). The markup rate is 25%.
Question 4.
Write an equation to determine the selling price in dollars, p, on an item that is originally priced s dollars after a markdown of 15%.
Answer:
p = 0.85s or p = (1 – 0.15)s
a. Create and label a table showing five possible pairs of solutions to the equation.
Answer:
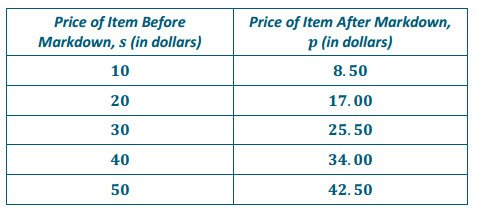
b. Create and label a graph of the equation.

Answer:
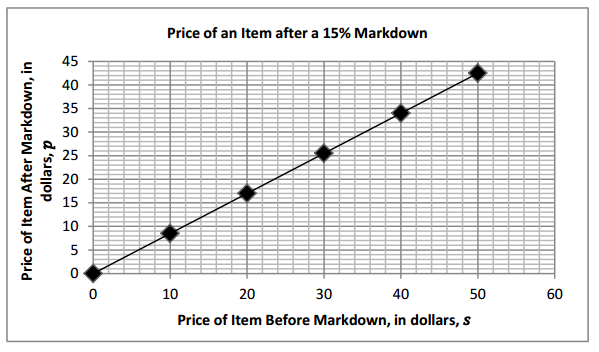
c. Interpret the points (0,0) and (1,r).
Answer:
The point (0, 0) means that a $0 (free) item will cost $0 because the 15% markdown is also $0. The point (1, r) is (1,0.85), which represents the unit rate. It means that a $1.00 item will cost $0.85 after it is marked down by 15%.
Question 5.
At the amusement park, Laura paid $6.00 for a small cotton candy. Her older brother works at the park, and he told her they mark up the cotton candy by 300%. Laura does not think that is mathematically possible. Is it possible, and if so, what is the price of the cotton candy before the markup?
Answer:
Yes, it is possible. \(\frac{6.00}{1 + 3}\) = \(\frac{6}{4}\) = 1.50. The price of the cotton candy before the markup is $1.50.
Question 6.
A store advertises that customers can take 25% off the original price and then take an extra 10% off. Is this the same as a 35% off discount? Explain.
Answer:
No, because the 25% is taken first off the original price to get a new whole. Then, the extra 10% off is multiplied to the new whole. For example, (1 – 0.25)(1 – 0.10) = 0.675 or (0.75)(0.90) = 0.675. This is multiplied to the whole, which is the original price of the item. This is not the same as adding 25% and 10% to get 35% and then multiplying by (1 – 0.35), or 0.65.
Question 7.
An item that costs $50.00 is marked 20% off. Sales tax for the item is 8%. What is the final price, including tax?
a. Solve the problem with the discount applied before the sales tax.
Answer:
(1.08)(0.80)(50) = 43.20. The final price is $43.20.
b. Solve the problem with the discount applied after the sales tax.
Answer:
(0.80)(1.08)(50) = 43.20. The final price is $43.20.
c. Compare your answers in parts (a) and (b). Explain.
Answer:
My answers are the same. The final price is $43.20. This is because multiplication is commutative.
Question 8.
The sale price for a bicycle is $315. The original price was first discounted by 50% and then discounted an additional 10%. Find the original price of the bicycle.
Answer:
(315 ÷ 0.9) ÷ 0.5 = 700. The original price was $700.
Question 9.
A ski shop has a markup rate of 50%. Find the selling price of skis that cost the storeowner $300.
Answer:
Solution 1: Use the original price of $300 as the whole. The markup rate is 50% of $300 or $150.
The selling price is $300 + $150 = $450.
Solution 2: Multiply $300 by 1 plus the markup rate (i.e., the selling price is (1.5)($300) = $450).
Question 10.
A tennis supply store pays a wholesaler $90 for a tennis racquet and sells it for $144. What is the markup rate?
Answer:
Solution 1: Let the original price of $90 be the whole. Quantity = Percent × Whole.
144 = Percent(90)
\(\frac{144}{90}\) = Percent
1.6 = 160%. This is a 60% increase. The markup rate is 60%.
Solution 2:
Selling Price = (1 + m)(Whole)
144 = (1 + m)90
1 + m = \(\frac{144}{90}\)
m = 1.6 – 1 = 0.6 = 60%
The markup rate is 60%.
Question 11.
A shoe store is selling a pair of shoes for $60 that has been discounted by 25%. What was the original selling price?
Answer:
Solution 1:
$60 → 75%
$20 → 25%
$80 → 100%
The original price was $80.
Solution 2: Let x be the original cost in dollars.
(1 – 0.25)x = 60
\(\frac{3}{4}\) x = 60
(\(\frac{4}{3}\))(\(\frac{3}{4}\) x) = \(\frac{4}{3}\) (60)
x = 80
The original price was $80.
Question 12.
A shoe store has a markup rate of 75% and is selling a pair of shoes for $133. Find the price the store paid for the shoes.
Answer:
Solution 1:
$133 → 175%
$19 → 25%
$76 → 100%
The store paid $76.
Solution 2: Divide the selling price by 1.75.
\(\frac{133}{1.75}\) = 76
The store paid $76.
Question 13.
Write 5 \(\frac{1}{4}\)% as a simple fraction.
Answer:
\(\frac{21}{400}\)
Question 14.
Write \(\frac{3}{8}\) as a percent.
Answer:
37.5%
Question 15.
If 20% of the 70 faculty members at John F. Kennedy Middle School are male, what is the number of male faculty members?
Answer:
(0.20)(70) = 14. Therefore, 14 faculty members are male.
Question 16.
If a bag contains 400 coins, and 33 1/2% are nickels, how many nickels are there? What percent of the coins are not nickels?
Answer:
(400)(0.335) = 134. Therefore, 134 of the coins are nickels. The percent of coins that are not nickels is 66 1/2%.
Question 17.
The temperature outside is 60 degrees Fahrenheit. What would be the temperature if it is increased by 20%?
Answer:
(60)(1.2) = 72. Therefore, the temperature would be 72 degrees Fahrenheit.
Eureka Math Grade 7 Module 4 Lesson 7 Exit Ticket Answer Key
A store that sells skis buys them from a manufacturer at a wholesale price of $57. The store’s markup rate is 50%.
a. What price does the store charge its customers for the skis?
Answer:
57 × (1 + 0.50) = 85.50. The store charges $85.50 for the skis.
b. What percent of the original price is the final price? Show your work.
Answer:
Quantity = Percent × Whole. Let P represent the unknown percent.
85.50 = P(57)
85.50(\(\frac{1}{57}\)) = P(57)(\(\frac{1}{57}\))
1.50 = P
1.50 = \(\frac{150}{100}\) = 150%. The final price is 150% of the original price
c. What is the percent increase from the original price to the final price?
Answer:
The percent increase is 50% because 150% – 100% = 50%.