Engage NY Eureka Math Grade 6 Module 5 Lesson 8 Answer Key
Eureka Math Grade 6 Module 5 Lesson 8 Example Answer Key
Question 1.
Plot and connect the points A(3, 2), B(3, 7), and C(8, 2). Name the shape, and determine the area of the polygon.

Answer:
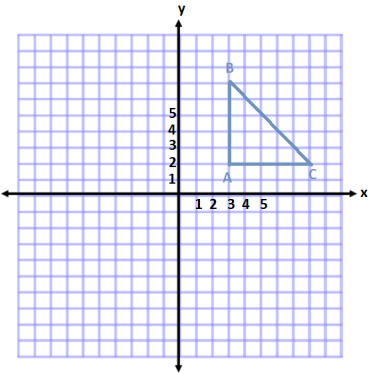
Right Triangle
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (5 units)(5 units)
A = \(\frac{1}{2}\) (25 units2)
A = 12.5 units2
Question 2.
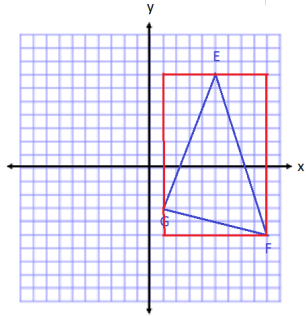
Plot and connect the points E(-8, 8), F(-2, 5), and G(-7, 2). Then give the best name for the polygon, and determine the area.
Answer:
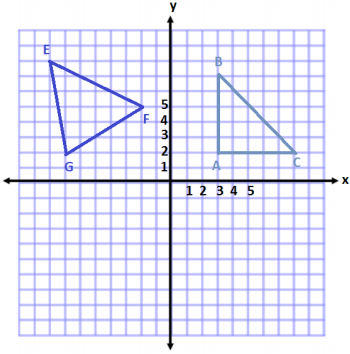
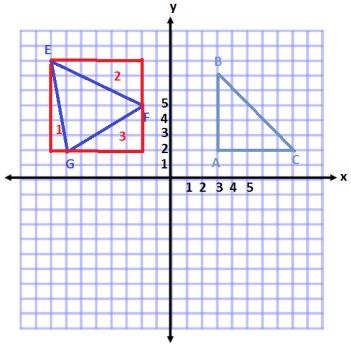
The shape is a triangle.
Area of Square
A = s2
A = (6 units)2
A = 36 units2
Area of Triangle 1
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (1 unit) (6 units)
A = \(\frac{1}{2}\) (6 units2)
A = 3 units2
Area of Triangle 2
A = \(\frac{1}{2}\)bh
A = \(\frac{1}{2}\) (6 units)(3 units)
A = \(\frac{1}{2}\) (18 units2)
A = 9 units2
Area of Triangle 3
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (5 units) (3 units)
A = \(\frac{1}{2}\) (15 units2)
A = 7.5 units2
Total Area of Triangle
A = 36 units2 – 3 units2 – 9 units2 – 7.5 units2
A = 16.5 units2
Question 3.
Plot and connect the following points: K(-9, -7), L(-4, -2), M(-1, -5), and N(-5, -5). Give the best name for the polygon, and determine the area.
Answer:
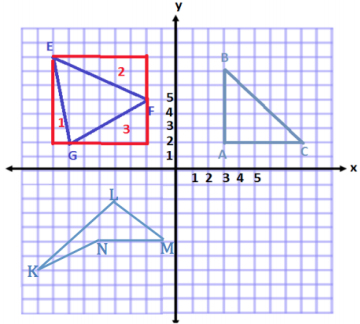
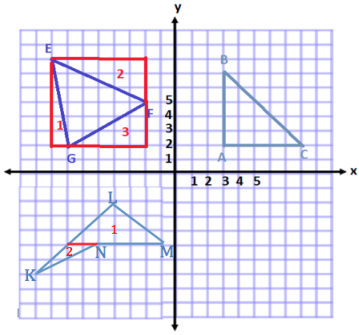
This polygon has 4 sides and has no pairs of parallel sides.
Therefore, the best name for this shape is a quadrilateral.
To determine the area, I will separate the shape into two
triangles.
Area of Triangle 1
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (6 units) (3 units)
A = \(\frac{1}{2}\) (18 units2)
A = 9 units2
Area of Triangle 2
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (2 units) (2 units)
A = \(\frac{1}{2}\) (4 units2)
A = 2 units2
Total Area = 9 units2 + 2 units2
Total Area = 11 units2
Question 4.
Plot and connect the following points: P(1, -4), Q(5, -2), R(9, -4), S(7, -8), and T(3, -8). Give the best name for the polygon, and determine the area.
Answer:
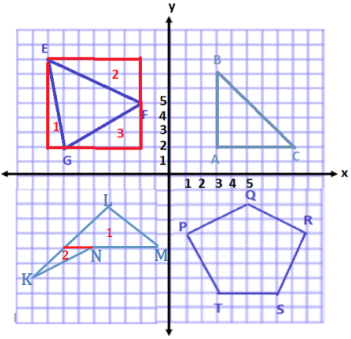
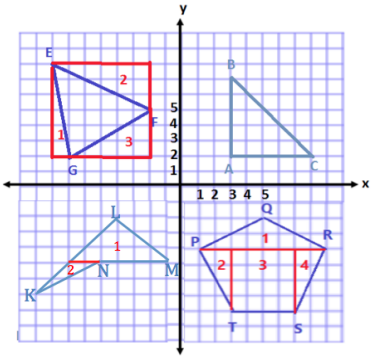
To determine the area, I will decompose this pentagon into four smaller shapes.
Area of Shape 1
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (8 units)(2 units)
A = \(\frac{1}{2}\) (16 units2)
A = 8 units2
Area of Shape 2 and Shape 4
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (4 units)(2 units)
A = \(\frac{1}{2}\) (8 units2)
A = 4 units2
Because there are two of the same triangle, that makes a total of 8 units2.
Area of Shape 3
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (4 units) (4 units)
A = 16 units2
Total Area = 8 units2 + 8 units2 + 16 units2
Total Area = 32 units2
Question 5.
Two of the coordinates of a rectangle are A (3, 7) and B (3, 2). The rectangle has an area of 30 square units. Give the possible locations of the other two vertices by identifying their coordinates. (Use the coordinate plane to draw and check your answer.)
Answer:
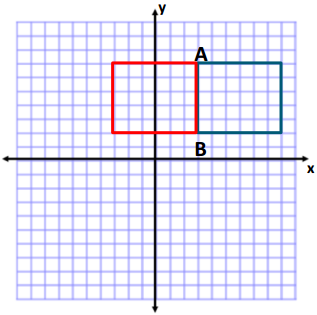
One possible location of the other two vertices is (9, 2) and (9, 7). Using these coordinates will result in a distance, or side length, of 6 units. Since the height is 5 units, 5 units × 6 units = 30 units2.
Another possible location of the other two vertices is (-3, 2) and (-3, 7). Using these coordinates will result in a distance, or side length, of 6 units. Since the height is 5 units, 5 units × 6 units = 30 units2.
Eureka Math Grade 6 Module 5 Lesson 8 Exercise Answer Key
Exercise:
For Exercises 1 and 2, plot the points, name the shape, and determine the area of the shape. Then write an expression that could be used to determine the area of the figure. Explain how each part of the expression corresponds to the situation.
Question 1.
A(4, 6), B(8, 6), C(10, 2), D(8, -3), E(5, -3), and F(2, 2)
Answer:
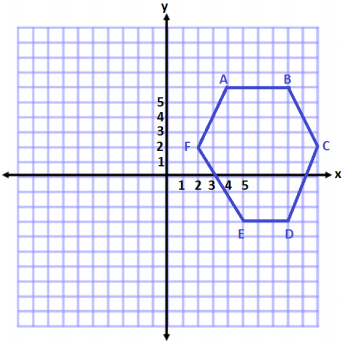
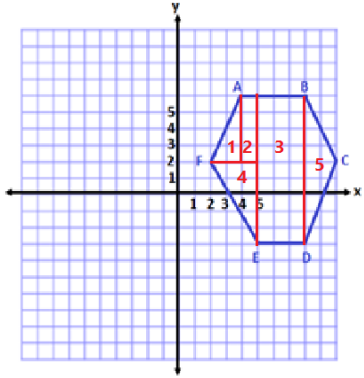
This shape is a hexagon.
Area of Shape 1
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (2 units)(4 units)
A = \(\frac{1}{2}\) (8 units2)
A = 4 units2
Area of Shape 2
A = \(\frac{1}{2}\) bh
A = (1 unit) (4 units)
A = 4 units2
Area of Shape 3
A = \(\frac{1}{2}\) bh
A = (3 units) (9 units)
A = 27 units2
Area of Shape 4
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (3 units)(5 units)
A = \(\frac{1}{2}\) (15 units2)
A = 7.5 units2
Area of Shape 5
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (2 units)(9 units)
A = \(\frac{1}{2}\) (18 units2)
A = 9 units2
Total Area = 4 units2 + 4 units2 + 27 units2 + 7.5 units2 + 9 units2
Expression:
\(\frac{1}{2}\) (2) (4) + (1) (4) + (3) (9) + \(\frac{1}{2}\) (3)(5) +\(\frac{1}{2}\) (2)(9).
Each term represents the area of a section of the hexagon. They must be added together to get the total.
The first term is the area of triangle 1 on the left.
The second term is the area of rectangle 2.
The third term is the area of the large rectangle 3.
The fourth term is the area of triangle 4 on the left.
The fifth term is the area of triangle 5 on the right.
Question 2.
X (-9, 6), Y (-2, -1), and Z (-8, -7)
Answer:

This shape is a triangle.
Area of Outside Rectangle
A = lw
A = (7 units) (13 units)
A = 91 units2
Area of Triangle 1
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (7 units)(7 units)
A = \(\frac{1}{2}\) (49 units2)
A = 24.5 units2
Area of Triangle 2
A = \(\frac{1}{2}\)bh
A = \(\frac{1}{2}\) (6 units)(6 units)
A = \(\frac{1}{2}\) (36 units2)
A = 18 units2
Area of Triangle 3
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (13 units)(1 unit)
A = \(\frac{1}{2}\) (13 units2)
A = 6.5 units2
Total Area = 91 units2 – 24.5 units2 – 18 units2 – 6.5 units2
Total Area = 42 units2
Expression:
(7)(13) – \(\frac{1}{2}\) (7)(7) – \(\frac{1}{2}\) (6)(6) – \(\frac{1}{2}\) (13)(1)
The first term in the expression represents the area of the rectangle that goes around the outside of the triangle.
The next three terms represent the areas that need to be subtracted from the rectangle so that we are only left with the given triangle.
The second term is the area of the top right triangle.
The third term is the area of the bottom right triangle.
The fourth term is the area of the triangle on the left.
Question 3.
A rectangle with vertices located at (-3, 4) and (5, 4) has an area of 32 square units. Determine the location of the other two vertices.
Answer:
The other two points could be located at (-3, 8) and (5, 8) or (-3, 0) and (5, 0).
Question 4.
Challenge: A triangle with vertices located at (-2, -3) and (3, -3) has an area of 20 square units. Determine one possible location of the other vertex.
Answer:
Answers will vary. Possible solutions include points that are 8 units from the base. (-2, 5) or (3, -11).
Eureka Math Grade 6 Module 5 Lesson 8 Problem Set Answer Key
Plot the points for each shape, determine the area of the polygon, and then write an expression that could be used to determine the area of the figure. Explain how each part of the expression corresponds to the situation.
Question 1.
A(1, 3), B(2, 8), C(8, 8), D(10, 3), and E(5, -2)
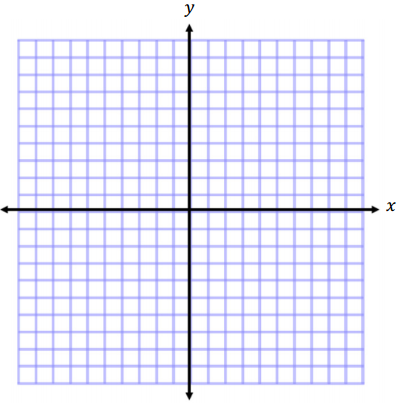
Answer:
Area of Triangle 1
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (6 units) (5 units)
A = \(\frac{1}{2}\) (30 units2)
A = 15 units2
Area of Triangle 2
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (9 units)(5 units)
A = \(\frac{1}{2}\) (45 units2)
A = 22.5 units2
Area of Triangle 3
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (9 units)(5 units)
A = \(\frac{1}{2}\) (45 units2)
A = 22.5 units2
Pentagon total area = 15 units2 + 22.5 units2 + 22.5 units2
Total Area = 60 units2
Expression:
\(\frac{1}{2}\) (6)(5) + \(\frac{1}{2}\) (9)(5) + \(\frac{1}{2}\) (9)(5)
Each term in the expression represents the area of one of the triangular pieces that fits inside the pentagon. They are all added together to form the complete figure.
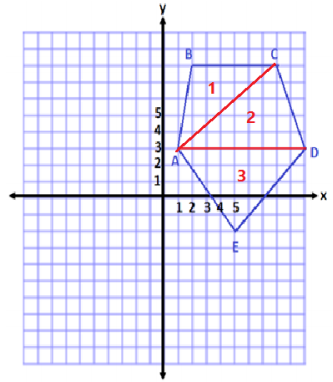
Question 2.
X(-10, 2), Y(-3, 6), and Z(-6, -5)

Answer:
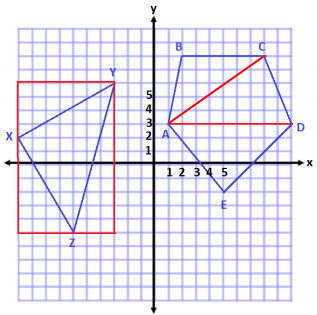
Area of Outside Rectangle
A = lw
A = (11 units) (7 units)
A = 77 units2
Area of Top Triangle
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (7 units)(4 units)
A = \(\frac{1}{2}\) (28 units2)
A = 14 units2
Area of Bottom Left Triangle
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (4 units)(7 units)
A = \(\frac{1}{2}\) (28 units2)
A = 14 units2
Area of Bottom Right Triangle
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (3 units)(11 units)
A = \(\frac{1}{2}\) (33 units2)
A = 16.5 units2
Area of center triangle = 77 units2 – 14 units2 – 14 units2 – 16.5 units2
Area of center triangle = 32.5 units2
Expression:
(11)(7) – \(\frac{1}{2}\) (7)(4) – \(\frac{1}{2}\) (4)(7) – \(\frac{1}{2}\) (3)(11)
The first term in the expression represents the area of the rectangle that would enclose the triangle. Then the three terms after represent the areas of the triangles that need to be removed from the area of the rectangle to find the area of the given triangle.
Question 3.
E(5, 7), F(9, -5), and G(1, -3)

Answer:
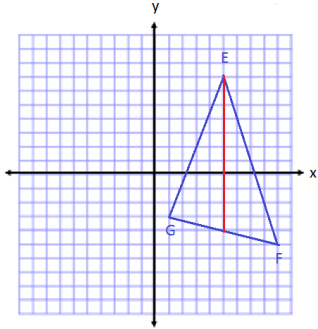
Area of Triangle on the Left
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (11 units)(4 units)
A = 22 units
Area of Triangle on the Right
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (11 units)(4 units)
A = 22 units2
Total Area = 22 units2 + 22 units2 = 44 units2
Expression:
\(\frac{1}{2}\) (11)(4) + \(\frac{1}{2}\) (11)(4)
Each term in the expression represents the area of a triangle that makes up the total area. The first term is the area of the triangle on the left, and the second term is the area of the triangle on the right.
Question 4.
Find the area of the triangle In Problem 3 using a different method. Then, compare the expressions that can be used for both solutions in Problems 3 and 4.
Answer:
Area of Rectangle
A = lw
A = (12 units) (8 units)
A = 96 units2
Area of Triangle on Top Left
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (4 units)(10 units)
A = 20 units2
Area of Triangle on Bottom Left
A =\(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (8 units)(2 units)
A = 8 units2
Area of Triangle on Right
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (4 units)(12 units)
A = 24 units2
Total Area = 96 units2 – 20 units2 – 8 units2 – 24 units2
Total Area = 44 units2
Expression: (12)(8) – \(\frac{1}{2}\) (4)(10) – \(\frac{1}{2}\) (8)(2) – \(\frac{1}{2}\) (4)(12)
The first term in the expression is the area of a rectangle around the outside of the figure. Then we subtracted all of the extra areas with the next three terms.
The two expressions are different because of the way we divided up the figure. In the first expression, we split the shape into two triangles that had to be added together to get the whole. In the second expression, we enclosed the triangle inside a new figure and then had to subtract the extra area.
Question 5.
Two vertices of a rectangle are (8, -5) and (8, 7). If the area of the rectangle is 72 square units, name the possible location of the other two vertices.
Answer:
(2, -5) and (2, 7) or (14, -5) and (14, 7)
Question 6.
A triangle with two vertices located at (5, -8) and (5, 4) has an area of 48 square units. Determine one possible location of the other vertex.
Answer:
Answers will vary. Possible solutions include points that are 8 units from the base such as (13, -2) or (-3, -2).
Eureka Math Grade 6 Module 5 Lesson 8 Exit Ticket Answer Key
Question 1.
Determine the area of both polygons on the coordinate plane, and explain why you chose the methods you used. Then write an expression that could be used to determine the area of the figure. Explain how each part of the expression corresponds to the situation.
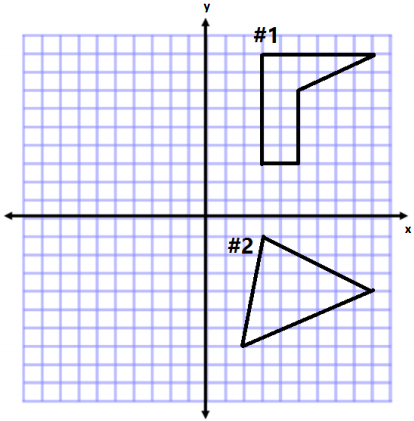
Answer:
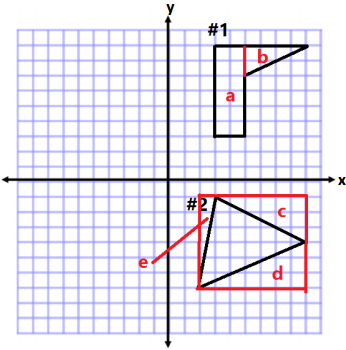
Methods to calculate the answer will vary.
#1 Area of shape a
A = lw
A = (2 units) (6 units)
A = 12 units2
Area of shape b
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (4 units)(2 units)
A = \(\frac{1}{2}\) (8 units2)
A = 4 units2
Total Area = 12 units2 + 4 units2 = 16 units2
Explanations will vary depending on the method chosen.
Expression: (2)(6) + latex]\frac{1}{2}[/latex] (4)(2)
The first term represents the area of the rectangle on the left, which makes up part of the figure.
The second term represents the area of the triangle on the right that completes the figure.
#2 Area of outside rectangle
A = lw
A = (7 units) (6 units)
A = 42 units2
Area of shape c
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (6 units)(3 units)
A = \(\frac{1}{2}\) (18 units2)
A = 9 units2
Area of shape d
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (7 units)(3 units)
A = \(\frac{1}{2}\) (21 units2)
A = 10.5 units2
Area of shape e
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (1 units)(6 units)
A = \(\frac{1}{2}\) (6 units2)
A = 3 units2
Total Area = 42 units2 – 9 units2 – 10.5 units2 – 3 units2
Total Area = 19.5 units2
Explanations will vary depending on method chosen.
Expression:
(7)(6) – \(\frac{1}{2}\) (6)(3) – \(\frac{1}{2}\) (7)(3) – \(\frac{1}{2}\) (1)(6)
The first term in the expression is the area of a rectangle that goes around the triangle.
Each of the other terms represents the triangles that need to be subtracted from the rectangle so that we are left with just the figure in the center.