Engage NY Eureka Math Grade 6 Module 5 Lesson 2 Answer Key
Eureka Math Grade 6 Module 5 Lesson 2 Exploratory Challenge Answer Key
Exploratory Challenge:
Question a.
Use the shapes labeled with an X to predict the formula needed to calculate the area of a right triangle. Explain your prediction.
Formula for the area of right triangles:
Area of the given triangle: ________
Answer:
Formula for the area of right triangles:
A = \(\frac{1}{2}\) × base × height or A = \(\frac{\text { base } \times \text { height }}{2}\)
Area of the given triangle:
A = \(\frac{1}{2}\) × 3 in. × 2 in. = 3 in2
Question b.
Use the shapes labeled with a Y to determine if the formula you discovered in part (a) is correct.
Does your area formula for triangle Y match the formula you got for triangle X?
Answer:
Answers will vary; however, the area formulas should be the same if students discovered the correct area
formula.
If so, do you believe you have the correct formula needed to calculate the area of a right triangle? Why or why not?
Answer:
Answers will vary.
If not, which formula do you think is correct? Why?
Answer:
Answers will vary.
Area of the given triangle:
A = \(\frac{1}{2}\) × 3 in. × 3 in. = 4.5 im <sup>2</sup>
Eureka Math Grade 6 Module 5 Lesson 2 Exercise Answer Key
Exercises:
Calculate the area of each right triangle below. Each figure is not drawn to scale.
Question 1.
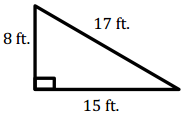
A = \(\frac{1}{2}\) bh
= \(\frac{1}{2}\) (8 ft.) (15 ft.)
= 60 ft2
Question 2.
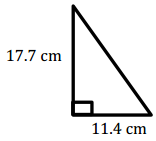
Answer:
A = \(\frac{1}{2}\) bh
= \(\frac{1}{2}\) (11.4 cm) (17.7 cm)
= 100.89 cm2
Question 3.
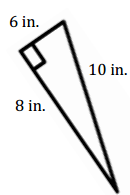
Answer:
A = \(\frac{1}{2}\) bh
= \(\frac{1}{2}\) (6 in.) (8 in.)
= 24 in2
Question 4.
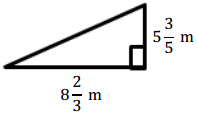
Answer:
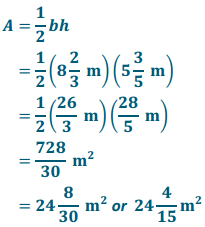
Question 5.
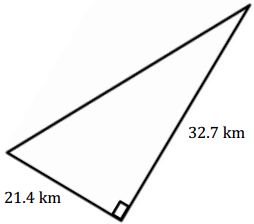
Answer:
A = \(\frac{1}{2}\) bh
= \(\frac{1}{2}\) (32.7 km) (21.4 km)
= 349.89 km2
Question 6.
Mr. Jones told his students they each need half of a piece of paper. Calvin cut his piece of paper horizontally, and Matthew cut his piece of paper diagonally. Which student has the larger area on his half piece of paper? Explain.
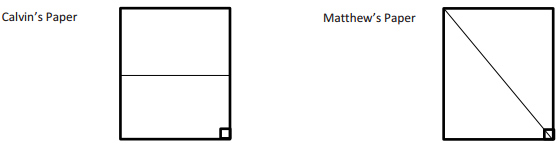
Answer:
After cutting the paper, both Calvin and Matthew have the same area. Calvin cut his into two rectangles that are each half the area of the original piece of paper. Matthew cut his paper into two equivalent right triangles that are also half the area of the original piece of paper.
Question 7.
Ben requested that the rectangular stage be split into two equal sections for the upcoming school play. The only instruction he gave was that he needed the area of each section to be half of the original size. If Ben wants the stage to be split into two right triangles, did he provide enough information? Why or why not?
Answer:
Ben did not provide enough information because the stage may be split horizontally or vertically through the middle of the rectangle. This would result in two equal pieces, but they would not be right triangles.
Question 8.
If the area of a right triangle is 6. 22 sq. in. and its base is 3. 11 in., write an equation that relates the area to the height, h, and the base. Solve the equation to determine the height.
Answer:
6.22 = \(\frac{1}{2}\) (3. 11)h
6.22 = (1.555)h
6.22 ÷ 1.555 = (1. 555)h ÷ 1.555
4 = h
Therefore, the height of the right triangle is 4 in.
Eureka Math Grade 6 Module 5 Lesson 2 Problem Set Answer Key
Calculate the area of each right triangle below. Note that the figures are not drawn to scale.
Question 1.
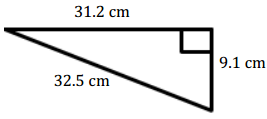
Answer:
A = \(\frac{1}{2}\) bh
= \(\frac{1}{2}\) (31.2 cm) (9.1 cm) = 141.96 cm2
Question 2.
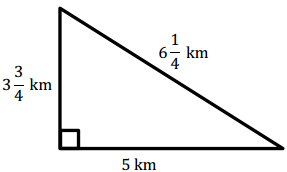
Answer:
![]()
Question 3.
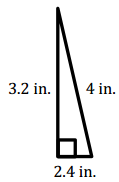
Answer:
A = \(\frac{1}{2}\) bh
= \(\frac{1}{2}\) (2.4 in.) (3.2 in.)
= 3.84 in2
Question 4.
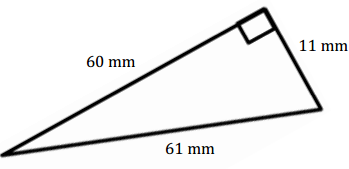
Answer:
A = \(\frac{1}{2}\) bh
= \(\frac{1}{2}\) (11 mm) (60 mm)
= 330 mm2
Question 5.
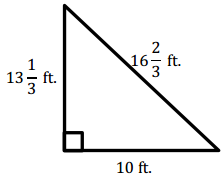
Answer:
![]()
Question 6.
Elania has two congruent rugs at her house. She cut one vertically down the middle, and she cut diagonally through the other one.
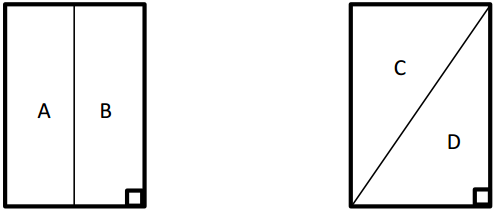
After making the cuts, which rug (labeled A, B, C, or D) has the larger area? Explain.
Answer:
All of the rugs are the same size after making the cuts. The vertical line goes down the center of the rectangle, making two congruent parts. The diagonal line also splits the rectangle into two congruent parts because the area of a right triangle is exactly half the area of the rectangle.
Question 7.
Give the dimensions of a right triangle and a parallelogram with the same area. Explain how you know.
Answer:
Answers will vary.
Question 8.
If the area of a right triangle is \(\frac{9}{16}\) sq. ft. and the height is \(\frac{3}{4}\) ft., write an equation that relates the area to the base, b, and the height. Solve the equation to determine the base.
Answer:
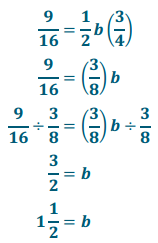
Therefore, the base of the right triangle is 1\(\frac{1}{2}\) ft.
Eureka Math Grade 6 Module 5 Lesson 2 Exit Ticket Answer Key
Question 1.
Calculate the area of the right triangle. Each figure is not drawn to scale.
Answer:
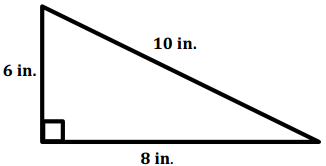
A = \(\frac{1}{2}\) bh = \(\frac{1}{2}\) (8 in.)(6 in.) = 24 in2
Question 2.
Dan and Joe are responsible for cutting the grass on the local high school soccer field. Joe cuts a diagonal line through the field, as shown in the diagram below, and says that each person is responsible for cutting the grass on one side of the line. Dan says that this is not fair because he will have to cut more grass than Joe. Is Dan correct? Why or why not?
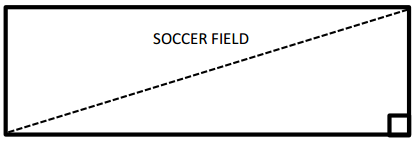
Answer:
Dan is not correct. The diagonal line Joe cut in the grass would split the field into two right triangles. The area of each triangle is exactly half the area of the entire field because the area formula for a right triangle is
A = \(\frac{1}{2}\) × base × height.