Engage NY Eureka Math Grade 6 Module 5 Lesson 10 Answer Key
Eureka Math Grade 6 Module 5 Lesson 10 Exercise Answer Key
Opening Exercise:
Question a.
Find the area and perimeter of this rectangle:
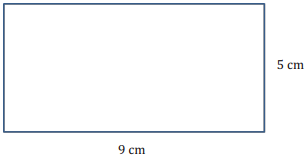
Answer:
A = bh = 9 cm × 5 cm = 45 cm2
P = 9 cm + 9 cm + 5 cm + 5 cm = 28 cm
Question b.
Find the width of this rectangle. The area is 1.2 m2, and the length is 1.5 m.

Answer:
A = l × w
1.2 m2 = 1.5 m × w
\(\frac{1.2 m^{2}}{1.5 m}\) = \(\frac{1.5 \mathrm{~m} \times \mathrm{w}}{1.5 \mathrm{~m}}\)
0.8 m = w
Eureka Math Grade 6 Module 5 Lesson 10 Example Answer Key
Example: Student Desks or Tables
Question 1.
Measure the dimensions of the top of your desk.
Answer:
Question 2.
How do you find the area of the top of your desk?
Answer:
Question 3.
How do you find the perimeter?
Answer:
Question 4.
Record these on your paper in the appropriate column.
Answer:
Exploratory Challenge:
Question 1.
Estimate and predict the area and perimeter of each object. Then measure each object, and calculate both the area and perimeter of each.
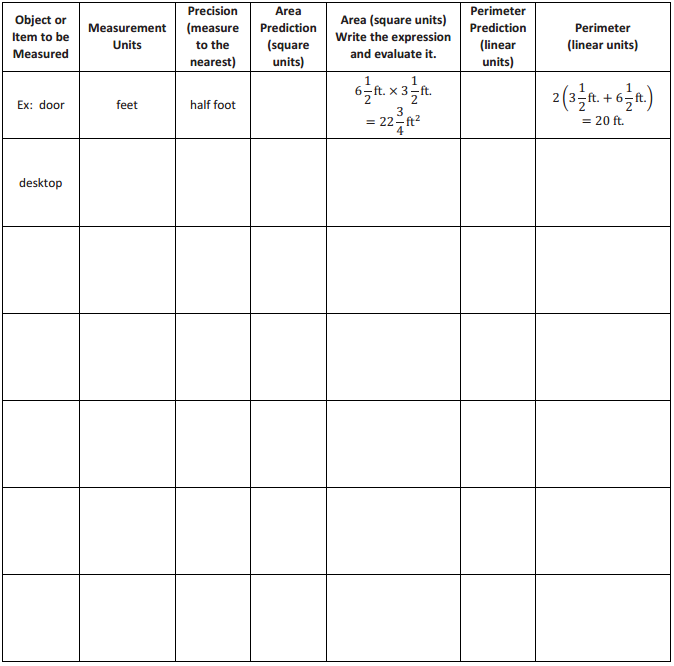
Answer:
Optional Challenge:
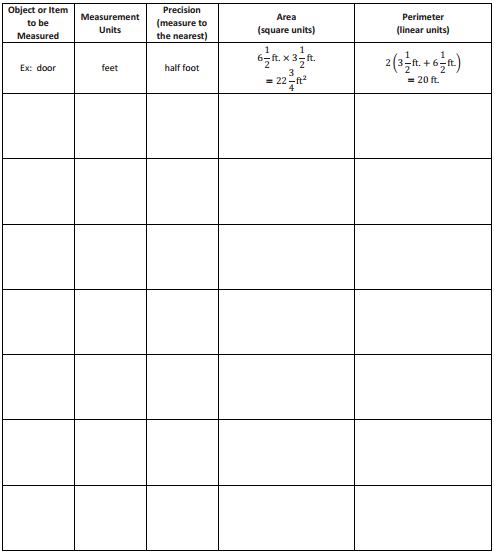
Answer:
Eureka Math Grade 6 Module 5 Lesson 10 Problem Set Answer Key
Question 1.
How is the length of the side of a square related to its area and perimeter? The diagram below shows the first four squares stacked on top of each other with their upper left-hand corners lined up. The length of one side of the smallest square is 1 foot.
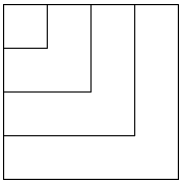
a. Complete this chart calculating area and perimeter for each square.
Answer:
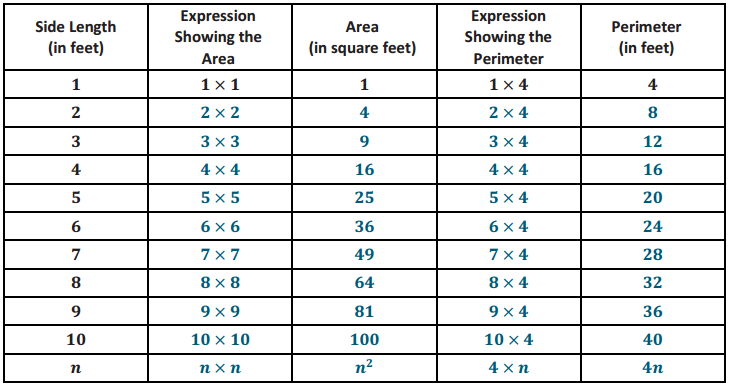
b. In a square, which numerical value is greater, the area or the perimeter?
Answer:
It depends. For side length less than 4 feet, perimeter is greater; however, for side length greater than 4 feet, area is greater.
c. When is the numerical value of a square’s area (in square units) equal to Its perimeter (in units)?
Answer:
When the side length is exactly 4 feet.
d. Why is this true?
Answer:
n2 = 4n is only true when n = 4.
Question 2.
This drawing shows a school pool. The walkway around the pool needs special non skid strips installed but only at the edge of the pool and the outer edges of the walkway.
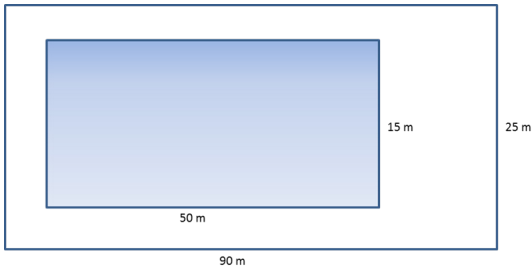
a. Find the length of nonskid strips that is needed for the job.
Answer:
50 m+ 50 m + 15 m + 15 m + 90 m + 90 m + 25 m + 25 m = 360 m
b. The nonskid strips are sold only in rolls of 50 m. How many rolls need to be purchased for the job?
Answer:
360 m ÷ 50 \(\frac{\mathrm{m}}{\text { roll }}\) = 7.2 rolls
Therefore, 8 rolls need to be purchased.
Question 3.
A homeowner called in a painter to paint the walls and ceiling of one bedroom. His bedroom is 18 ft. long, 12 ft. wide, and 8 ft. high. The room has two doors, each 3 ft. by 7 ft., and three windows each 3 ft. by 5 ft. The doors and windows will not be painted. A gallon of paint can cover 300 ft2. A hired painter claims he needs a minimum of 4 gallons. Show that his estimate is too high.
Answer:
Area of 2 long walls: 2(18 ft. × 8 ft.) = 288 ft2
Area of 2 short walls: 2(12 ft. × 8 ft.) = 192 ft2
Area of ceiling: 18 ft. × 12 ft. = 216 ft2
Area of2 doors: 2(3 ft. × 7 ft.) 42 ft2
Area of 3 windows: 3(3 ft. × 5 ft.) = 45 ft2
Area to be painted: (288 ft2 + 192 ft2 + 216 ft2) – (42 ft2 + 45 ft22) = 609 ft2
Gallons of point needed: 609 + 300 = 2.03
The painter will need a little more than 2 gallons. The pointer’s estimate for how much paint Is necessary was too high.
Question 4.
Theresa won a gardening contest and was awarded a roll of deer-proof fencing. The fencing is 36 feet long. She and her husband, John, discuss how to best use the fencing to make a rectangular garden. They agree that they should only use whole numbers of feet for the length and width of the garden.
a. What are all of the possible dimensions of the garden?
Answer:
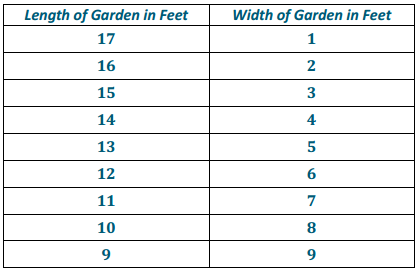
b. Which plan yields the maximum area for the garden? Which plan yields the minimum area?
Answer:
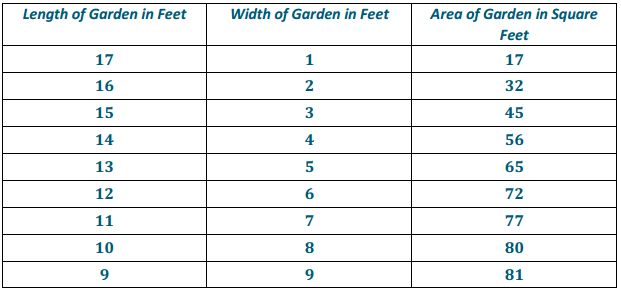
The 9 ft. by 9 ft. garden would have the maximum area (81 ft2), while the 17 ft. by 1 ft. garden would have only 17 ft2 of garden space.
Question 5.
Write and then solve the equation to find the missing value below.
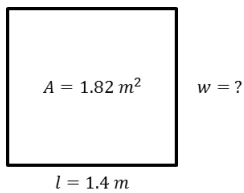
Answer:
A = l × w
182 m2 = 1.4m × w
\(\frac{1.82 \mathrm{~m}^{2}}{1.4 \mathrm{~m}}\) = w
1.3 m = w
Question 6.
Challenge: This is a drawing of the flag of the Republic of the Congo. The area of this flag is 3\(\frac{3}{4}\) ft2.
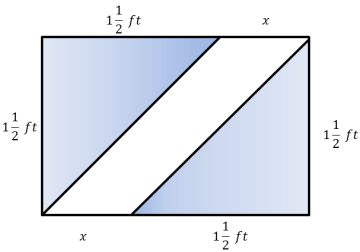
a. Using the area formula, tell how you would determine the value of the base. This figure is not drawn to scale.
Answer:
A = bh
A ÷ h = b
3\(\frac{3}{4}\) ft2 ÷ 1\(\frac{1}{2}\)ft. = b
2\(\frac{1}{2}\) ft. = b
b. Using what you found in part (a), determine the missing value of the base.
Ans:
2\(\frac{1}{2}\) ft. = 1\(\frac{1}{2}\) ft. + x
1 ft. = x
Eureka Math Grade 6 Module 5 Lesson 10 Exit Ticket Answer Key
Question 1.
The local school is building a new playground. This plan shows the part of the playground that needs to be framed with wood for the swing set. The unit of measure is feet. Determine the number of feet of wood needed to frame the area.
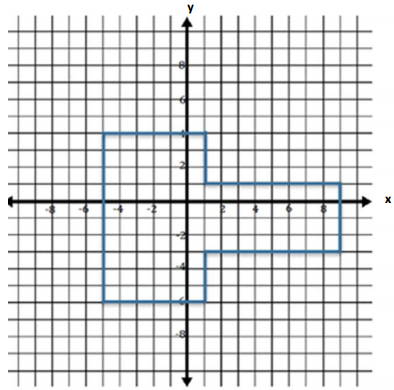
Answer:
Perimeter: 10 ft. + 6 ft. + 6 ft. + 3 ft. + 3 ft. + 8 ft. + 8 ft. + 4 ft. = 48 ft.
Question 2.
The school wants to fill the area enclosed with wood with mulch for safety. Determine the number of square feet that needs to be covered by the mulch.
Answer:

Area of Left Rectangle = bh = (6 ft. x 10 ft.) = 60 ft2
Area of Right Rectangle = bh = (8 ft. X 4 ft.) = 32 ft2
Total Area = 60 ft2 + 32 ft2 = 92 ft2