Engage NY Eureka Math Grade 6 Module 4 Lesson 30 Answer Key
Eureka Math Grade 6 Module 4 Lesson 30 Opening Exercise Answer Key
Opening Exercise:
Draw an example of each term, and write a brief description.
Acute:
Answer:
Less than 90°
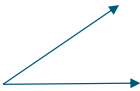
Obtuse
Answer:
Between 90° and 180°
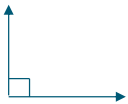
Right
Answer:
Exactly 90°
Straight
Answer:
Exactly 180°
![]()
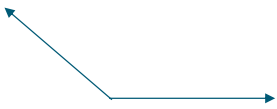
Reflex
Answer:
Between 180° and 360°
Eureka Math Grade 6 Module 4 Lesson 30 Example Answer Key
Example 1:
∠ABC measures 90°. The angle has been separated into two angles. If one angle measures 57°, what is the measure of the other angle?
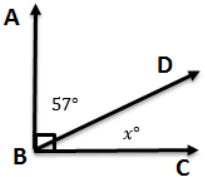
Answer:
In this lesson, we will be using algebra to help us determine unknown measures of angles.
How are these two angles related?
Answer:
x° + 57° = 90°
What equation could we use to solve for x?
Answer:
Now, let’s solve.
x° + 57° – 57° = 90° – 57°
x° = 33°
The measure of the unknown angle is 33°.
Example 2:
Michelle is designing a parking lot. She has determined that one of the angles should be 115°. What is the measure of angle x and angle y?
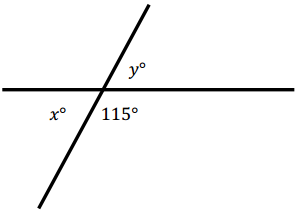
How is angle x related to the 115° angle?
Answer:
The two angles form o straight line. Therefore, they should add up to 180°.
What equation would we use to show this?
Answer:
x° + 115° = 180°
How would you solve this equation?
Answer:
115° was added to angle x, so I will take away 115° to get back to angle X.
x° + 115° – 115° = 180° – 115°
x° = 65°
The angle next to 115°, labeled with an x, is equal to 65°.
How is angle y related to the angle that measures 115°?
Answer:
These two angles also form a straight line and must add up to 180°.
Therefore, angles x and y must both be equal to 65°.
Example 3:
A beam of light is reflected off a mirror. Below is a diagram of the reflected beam. Determine the missing angle measure.
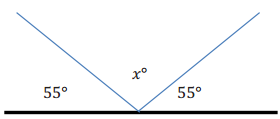
How are the angles in this question-related?
Answer:
There are three angles that, when all placed together, form a straight line. This means that the three angles have a sum of 180°.
What equation could we write to represent the situation?
Answer:
55° + x + 55° = 180°
How would you solve an equation like this?
Answer:
We can combine the two angles that we do know.
55° + 550 + x° = 180°
110° + x° = 180°
110° – 110° + x° = 180° – 110°
x° = 70°
The angle of the bounce is 70°.
Example 4:
∠ABC measures 90°. It has been split into two angles, ∠ABD and ∠DBC. The measure of ∠ABD and ∠DBC is in a ratio of 4: 1. What are the measures of each angle? Use a tape diagram to represent the ratio 4: 1.
What is the measure of each angle?
5 units = 90°
1 unit = 18°
4 units = 72°
∠ABD is 72°. ∠DBC is 18°
How can we represent this situation with an equation?
Answer:
4x° + x° = 90°
Solve the equation to determine the measure of each angle.
4x° + x° = 90°
5x° = 90°
5x° ÷ 5 = 90° ÷ 5
x° = 18°
4x° = 4(18°) = 72°
The measure of ∠DBC is 18° and the measure of ∠ABD is 72°.
Eureka Math Grade 6 Module 4 Lesson 30 Exercise Answer Key
Exercises:
Write and solve an equation in each of the problems.
Exercise 1.
∠ABC measures 900. It has been split into two angles, ∠ABD and ∠DBC. The measure of the two angles is in a ratio of 2: 1. What are the measures of each angle?
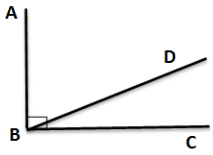
Answer:
x° + 2x° = 90°
3x° = 90°
\(\frac{3 x^{\circ}}{3}=\frac{90^{\circ}}{3}\)
x° = 30°
One of the angles measures 30°, and the other measures 60°.
Exercise 2.
Solve for x.
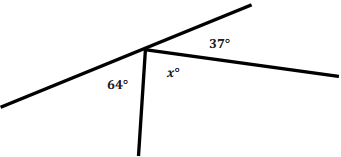
Answer:
x° + 64° + 37° = 180°
x° + 101° = 180°
x° + 101° – 101° = 180° – 101°
x° = 79°
Exercise 3.
Candice is building a rectangular piece of a fence according to the plans her boss gave her. One of the angles is not labeled. Write an equation, and use it to determine the measure of the unknown angle.
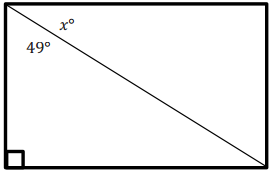
Answer:
x° + 49° = 90°
x° + 49° – 49° = 90° – 49°
x° = 41°
Exercise 4.
Rashid hit a hockey puck against the wall at a 38° angle. The puck hit the wall and traveled in a new direction. Determine the missing angle in the diagram.
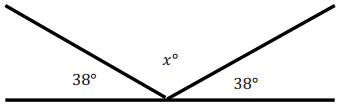
Answer:
38° + x° + 38° = 180°
76° + x° = 180°
76° – 76° + x° = 180° – 76°
x° = 104°
The measure of the missing angle is 104°.
Exercise 5.
Jaxon is creating a mosaic design on a rectangular table. He has added two pieces to one of the corners. The first piece has an angle measuring 38° and is placed in the corner. A second piece has an angle measuring 27° and is also placed in the comer. Draw a diagram to model the situation. Then, write an equation, and use it to determine the measure of the unknown angle in a third piece that could be added to the corner of the table.
Answer:
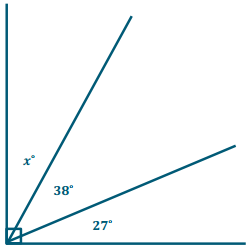
x° + 38° + 27° = 90°
x° + 65° = 90°
x° + 65° – 65° = 90° – 65°
x° = 25°
The measure of the unknown angle is 25°.
Eureka Math Grade 6 Module 4 Lesson 30 Problem Set Answer Key
Write and solve an equation for each problem.
Question 1.
Solve for x.
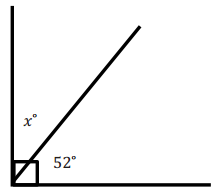
Answer:
x° + 52° = 90°
x° + 52° – 52° = 90° – 52°
x° = 38°
The measure of the missing angle is 38°
Question 2.
∠BAE measures 90°. Solve for x.
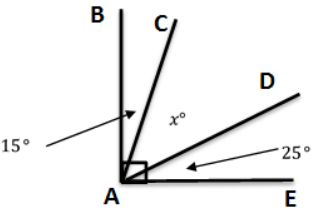
Answer:
15° + x + 25° = 90°
15° + 25° + x = 90
40° + x = 90°
40° – 40° + x = 90°
x° = 50°
Question 3.
Thomas is putting in a tile floor. He needs to determine the angles that should be cut in the tiles to fit in the comer. The angle in the comer measures 90°. One piece of the tile will have a measure of 24°. Write an equation, and use it to determine the measure of the unknown angle.
Answer:
x° + 24° = 90°
x° + 24° – 24° = 90° – 24°
x° = 66°
The measure of the unknown angle is 66°.
Question 4.
Solve for x°.
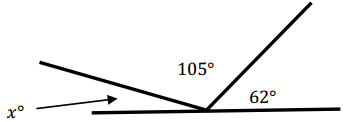
Answer:
x° + 105° + 62° = 180°
x° + 167° = 180°
x° + 167° – 167° = 180° – 167°
x° = 13°
The measure of the missing angle is 13°.
Question 5.
Aram has been studying the mathematics behind pinball machines. He made the following diagram of one of his
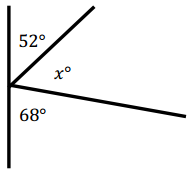
Answer:
52° + x° + 68° = 180°
120° + x° = 180°
120° + x° – 120° = 180° – 120°
x° = 60°
The measure of the missing angle is 60°.
Question 6.
The measures of two angles have a sum of 90°. The measures of the angles are in a ratio of 2: 1. Determine the measures of both angles.
Answer:
2x° + x° = 90°
3x° = 90°
\(\frac{3 x^{\circ}}{3}=\frac{90^{\circ}}{3}\)
x° = 30°
The angles measure 30° and 60°.
Question 7.
The measures of two angles have a sum of 1800. The measures of the angles are in a ratio of 5: 1. Determine the measures of both angles.
Answer:
5x° + x° = 180°
6x° = 180°
\(\frac{6 x^{\circ}}{6}=\frac{180}{6}\)
x° = 30°
The angles measure 30° and 150°.
Eureka Math Grade 6 Module 4 Lesson 30 Exit Ticket Answer Key
Write an equation, and solve for the missing angle in each question.
Question 1.
Alejandro is repairing a stained glass window. He needs to take ft apart to repair ft. Before taking ft apart, he makes a sketch with angle measures to put ft back together. Write an equation, and use ft to determine the measure of the unknown angle.
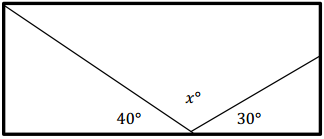
Answer:
40° + x° + 30° = 180°
x° + 40° + 30° = 180°
x° + 70° = 180°
x° + 70° – 70° = 180° – 70°
x° = 110°
The missing angle measures 110°.
Question 2.
Hannah is putting in a tile floor. She needs to determine the angles that should be cut in the tiles to fit in the corner. The angle in the comer measures 90°. One piece of the tile will have a measure of 38°. Wrfte an equation, and use it to determine the measure of the unknown angle.
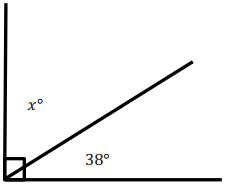
Answer:
x° + 38° = 90°
38° – 38° = 90° – 38°
x° = 52°
The measure of the unknown angle is 52°.
Eureka Math Grade 6 Module 4 Lesson 30 Subtraction of Decimals Answer Key
Subtraction of Decimals – Round 1:
Directions: Evaluate each expression.
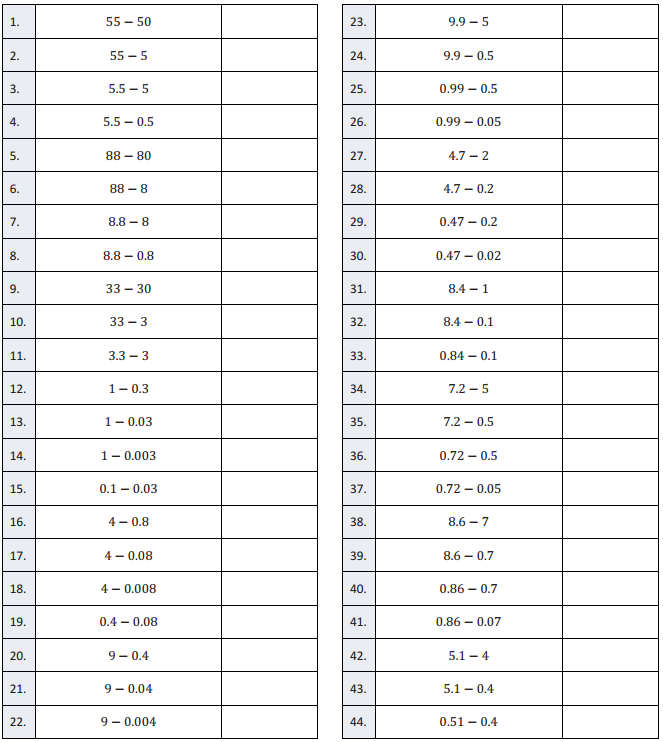
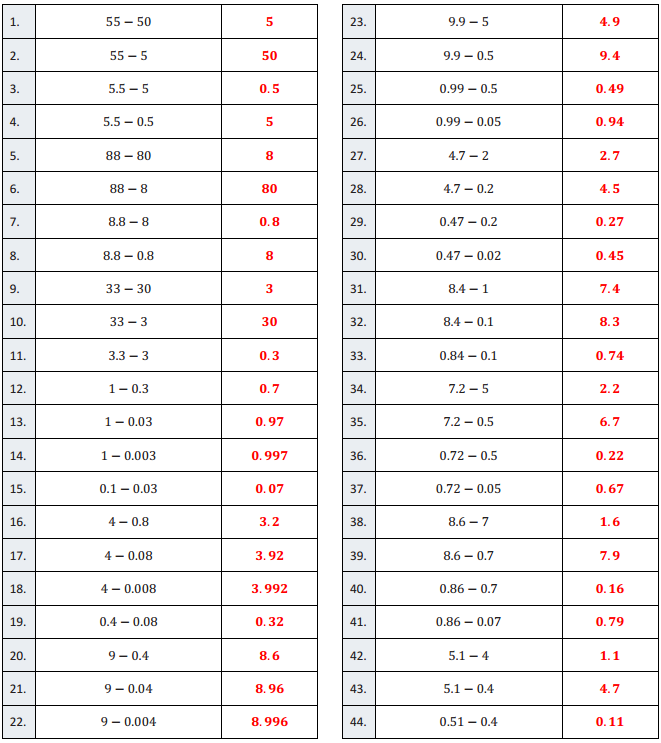
Question 1.
55 – 50
Answer:
5
Question 2.
55 – 5
Answer:
50
Question 3.
5.5 – 5
Answer:
0.5
Question 4.
5.5 – 0.5
Answer:
5.0
Question 5.
88 – 80
Answer:
8
Question 6.
88 – 8
Answer:
80
Question 7.
8.8 – 8
Answer:
0.8
Question 8.
8.8 – 0.8
Answer:
8
Question 9.
33 – 30
Answer:
3
Question 10.
33 – 3
Answer:
30
Question 11.
3.3 – 3
Answer:
0.3
Question 12.
1 – 0.3
Answer:
0.7
Question 13.
1 – 0.03
Answer:
0.97
Question 14.
1 – 0.003
Answer:
0.997
Question 15.
0.1 – 0.03
Answer:
0.07
Question 16.
4 – 0.8
Answer:
3.2
Question 17.
4 – 0.08
Answer:
3.92
Question 18.
4 – 0.008
Answer:
3.992
Question 19.
0.4 – 0.08
Answer:
0.32
Question 20.
9 – 0.4
Answer:
8.6
Question 21.
9 – 0.04
Answer:
8.96
Question 22.
9 – 0.004
Answer:
8.996
Question 23.
9.9 – 5
Answer:
4.9
Question 24.
9.9 – 0.5
Answer:
9.4
Question 25.
0.99 – 0.5
Answer:
0.49
Question 26.
0.99 – 0.05
Answer:
0.94
Question 27.
4.7-2
Answer:
Question 28.
4.7 – 0.2
Answer:
4.5
Question 29.
0.47 – 0.2
Answer:
0.27
Question 30.
0.47 – 0.02
Answer:
0.45
Question 31.
8.4 – 1
Answer:
7.4
Question 32.
8.4 – 0.1
Answer:
8.3
Question 33.
0.84 – 0.1
Answer:
0.83
Question 34.
7.2 – 5
Answer:
5.2
Question 35.
7.2 – 0.5
Answer:
6.7
Question 36.
0.72 – 0.5
Answer:
0.22
Question 37.
0.72 – 0.05
Answer:
0.67
Question 38.
8.6 – 7
Answer:
1.6
Question 39.
8.6 – 0.7
Answer:
7.9
Question 40.
0.86 – 0.7
Answer:
0.16
Question 41.
0.86 – 0.07
Answer:
0.79
Question 42.
5.1 – 4
Answer:
1.1
Question 43.
5.1 – 4.7
0.4
Answer:
Question 44.
0.51 – 0.4
Answer:
0.11
Subtraction of Decimals-Round 2:
Directions: Evaluate each expression:
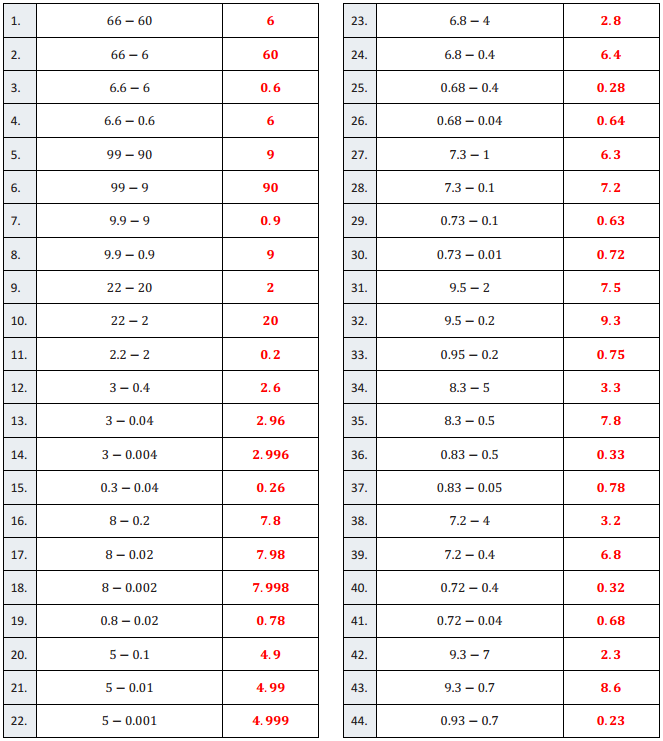
Question 1.
66 – 60
Answer:
6
Question 2.
66 – 6
Answer:
60
Question 3.
6.6 – 6
Answer:
0.6
Question 4.
6.6 – 0.6
Answer:
6
Question 5.
99 – 90
Answer:
9
Question 6.
99 – 9
Answer:
90
Question 7.
9.9 – 9
Answer:
0.9
Question 8.
9.9 – 0.9
Answer:
9
Question 9.
22 – 20
Answer:
2
Question 10.
22 – 2
Answer:
20
Question 11.
2.2 – 2
Answer:
0.2
Question 12.
3 – 0.4
Answer:
2.6
Question 13.
3 – 0.04
Answer:
2.96
Question 14.
3 – 0.004
Answer:
2.996
Question 15.
0.3 – 0.04
Answer:
0.26
Question 16.
8 – 0.2
Answer:
7.8
Question 17.
8 – 0.02
Answer:
7.98
Question 18.
8 – 0.002
Answer:
7.998
Question 19.
0.8 – 0.02
Answer:
0.78
Question 20.
5 – 0.1
Answer:
4.9
Question 21.
5 – 0.01
Answer:
4.99
Question 22.
5 – 0.001
Answer:
4.999
Question 23.
6.8 – 4
Answer:
2.8
Question 24.
6.8 – 0.4
Answer:
6.4
Question 25.
0.68 – 0.4
Answer:
0.28
Question 26.
0.68 – 0.04
Answer:
0.64
Question 27.
7.3 – 1
Answer:
6.3
Question 28.
7.3 – 0.1
Answer:
7.2
Question 29.
0.73 – 0.1
Answer:
0.63
Question 30.
0.73 – 0.01
Answer:
0.72
Question 31.
9.5 – 2
Answer:
7.5
Question 32.
9.5 – 0.2
Answer:
9.3
Question 33.
0.95 – 0.2
Answer:
0.75
Question 34.
8.3 – 5
Answer:
3.3
Question 35.
8.3 – 0.5
Answer:
7.8
Question 36.
0.83 – 0.5
Answer:
0.33
Question 37.
0.83 – 0.05
Answer:
0.78
Question 38.
7.2 – 4
Answer:
3.2
Question 39.
7.2 – 0.4
Answer:
6.8
Question 40.
0.72 – 0.4
Answer:
0.32
Question 41.
0.72 – 0.04
Answer:
0.68
Question 42.
9.3 – 7
Answer:
2.3
Question 43.
9.3 – 0.7
Answer:
8.6
Question 44.
0.93 – 0.7
Answer:
0.23