Engage NY Eureka Math Grade 6 Module 4 Lesson 27 Answer Key
Eureka Math Grade 6 Module 4 Lesson 27 Example Answer Key
Example 1:
Solve 3z = 9 using tape diagrams and algebraically. Then, check your answer. First, draw two tape diagrams, one to represent each side of the equation.
Answer:

If 9 had to be split into three groups, how big would each group be?
Answer:
3
Demonstrate the value of z using tape diagrams.
Answer:

How can we demonstrate this algebraically?
Answer:
We know we have to split 9 into three equal groups, so we have to divide by 3 to show this algebraically.
3z ÷ 3 = 9 ÷ 3
How does this get us the value of z?
Answer:
The left side of the equation will equal z because we know the identity property, where a . b ÷ b = a, so we con use this identity here.
The right side of the equation will be 3 because 9 ÷ 3 = 3.
Therefore, the value of z is 3.
How can we check our answer?
Answer:
We can substitute the value of z into the original equation to see if the number sentence is true.
3(3) = 9; 9 = 9. This number sentence is true, so our answer is correct.
Example 2:
Solve \(\frac{y}{4}\) = 2 using tape diagrams and algebraically. Then, check your answer. First, draw two tape diagrams, one to represent each side of the equation.
Answer:

If the first tape diagram shows the size of y ÷ 4, how can we draw a tape diagram to represent y?
Answer:
The tape diagram to represent y should be four sections of the size y ÷ 4.
Draw this tape diagram.
Answer:

What value does each y ÷ 4 section represent? How do you know?
Answer:
Each y ÷ 4 section represents a value of 2. We know this from our original tape diagram.
How can you use a tape diagram to show the value of y?
Answer:
Draw four equal sections of 2, which will give y the value of 8.
![]()
How can we demonstrate this algebraically?
Answer:
\(\frac{y}{4}\) . 4 = 2 . 4. Because we multiplied the number of sections in the original equation by 4, we know the identity
\(\frac{a}{b}\) . b = a can be used here.
How does this help us find the value of y?
Answer:
The left side of the equation will equal y, and the right side will equal 8. Therefore, the value of y is 8.
How can we check our answer?
Answer:
Substitute 8 into the equation for y, and then check to see if the number sentence is true.
\(\frac{8}{4}\) = 2. This is a true number sentence, so 8 is the correct answer.
Eureka Math Grade 6 Module 4 Lesson 27 Exercise Answer Key
Exercises:
Exercise 1.
Use tape diagrams to solve the following problem: 3m = 21.
Answer:
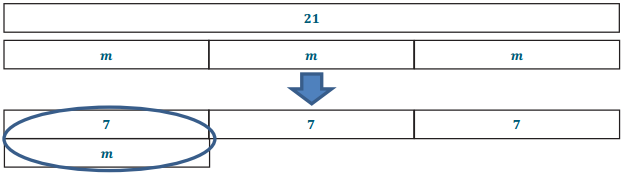
check: 3(7) = 21; 21 = 21. This number sentence is true, so 7 is the correct solution.
Exercise 2.
Solve the following problem algebraically: 15 = \(\frac{n}{5}\)
Answer:
15 = \(\frac{n}{5}\)
15 . 5 = \(\frac{n}{5}\) . 5
75 = n
Check: 15 = \(\frac{75}{5}\); 15 = 15. This number sentence is true, so 75 is the correct solution.
Exercise 3.
Calculate the solution of the equation using the method of your choice: 4p = 36.
Answer:
Tape Diagrams:
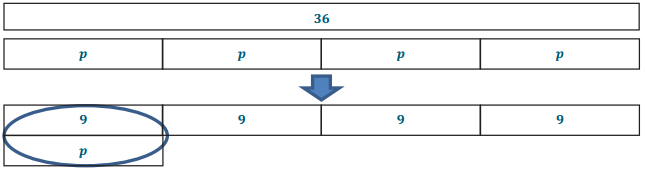
Algebraically:
4p = 36
4p ÷ 3 = 36 ÷ 4
p = 9
Check:
4(9) = 36; 36 = 36. This number sentence is true, so 9 is the correct solution.
Exercise 4.
Examine the tape diagram below, and write an equation it represents. Then, calculate the solution to the equation using the method of your choice.

Answer:

Algebraically:
7q = 70
7q ÷ 7 = 70 ÷ 7
q = 10
70 = 7q
70 ÷ 7 = 7q ÷ 7
q = 10
Check:
7(10) = 70, 70 = 7(10); 70 = 70. This number sentence is true, so 10 is the correct answer.
Exercise 5.
Write a multiplication equation that has a solution of 12. Use tape diagrams to prove that your equation has a solution of 12.
Answer:
Answers will vary.
Exercise 6.
Write a division equation that has a solution of 12. Prove that your equation has a solution of 12 using algebraic methods.
Answer:
Answers will vary.
Eureka Math Grade 6 Module 4 Lesson 27 Problem Set Answer Key
Question 1.
Use tape diagrams to calculate the solution of 30 = 5w. Then, check your answer.
Answer:
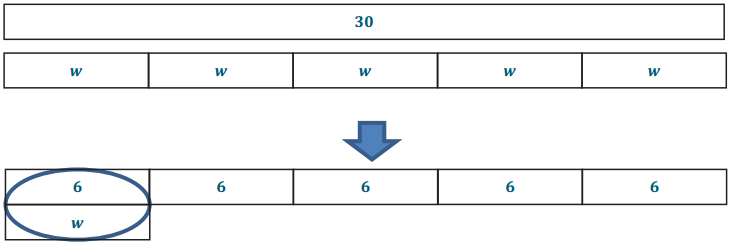
Check: 30 = 5(6); 30 = 30. This number sentence is true, so 6is the correct solution.
Question 2.
Solve 12 = \(\frac{x}{4}\) algebraically. Then, check your answer.
Answer:
12 = \(\frac{x}{4}\)
12 . 4 = \(\frac{x}{4}\) . 4
48 = x
Check:
12 = \(\frac{48}{4}\); 12 = 12. This number sentence is true, so 48 is the correct solution.
Question 3.
Use tape diagrams to calculate the solution of \(\frac{y}{5}\) = 15. Then, check your answer.
Answer:
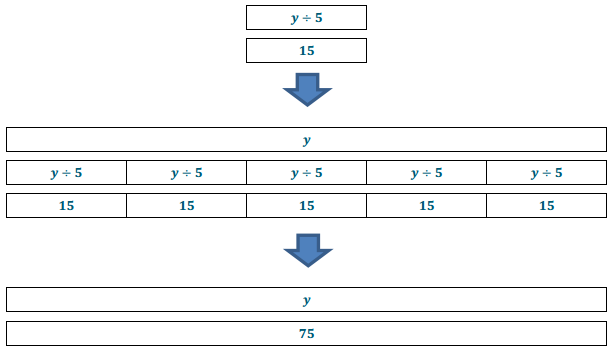
Check:
\(\frac{75}{5}\) = 15; 15 = 15. This number sentence is true, so 75 is the correct solution.
Question 4.
Solve 18z = 72 algebraically. Then, check your answer.
Answer:
18z = 72
18z ÷ 18 = 72 ÷ 18
z = 4
Check:
18(4) = 72; 72 = 72. This number sentence is true, so 4 is the correct solution.
Question 5.
Write a division equation that has a solution of 8. Prove that your solution is correct by using tape diagrams.
Answer:
Answers will vary.
Question 6.
Write a multiplication equation that has a solution of 8. Solve the equation algebraically to prove that your solution is correct.
Answer:
Answers will vary.
Question 7.
When solving equations algebraically, Meghan and Meredith each got a different solution. Who is correct? Why did the other person not get the correct answer?
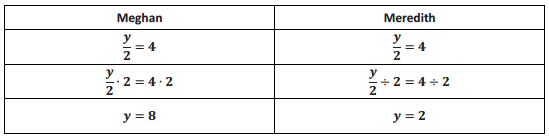
Answer:
Meghan is correct. Meredith divided by 2 to solve the equation, which is not correct because she would end up with \(\frac{y}{4}\) = 2. To solve a division equation, Meredith must multiply by 2 to end up with y because the identity states.
y ÷ 2 . 2 = y.
Eureka Math Grade 6 Module 4 Lesson 27 Exit Ticket Answer Key
Calculate the solution to each equation below using the indicated method. Remember to check your answers.
Question 1.
Use tape diagrams to find the solution of \(\frac{r}{10}\) = 4.
Answer:
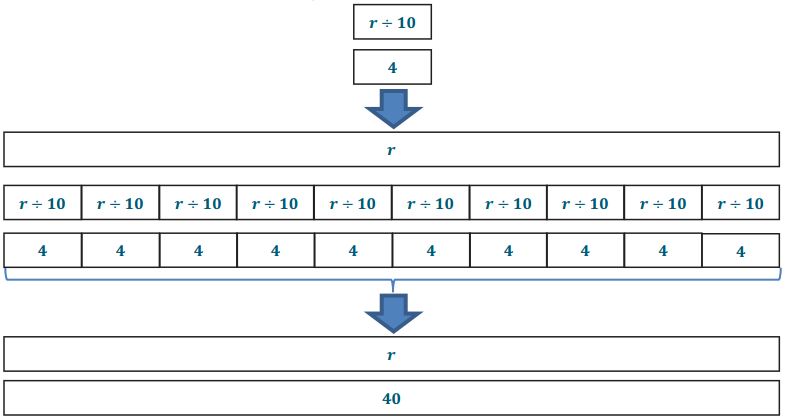
Check:
\(\frac{40}{10}\) = 4; 4 = 4. This number sentence is true, so 40 is the correct solution.
Question 2.
Find the solution of 64 = 16u algebraically.
Answer:
64 = 16u
64 ÷ 16 = 16u ÷ 16
4 = u
Check:
64 = 16(4); 64 = 64. This number sentence is true, so 4 is the correct solution.
Question 3.
Use the method of your choice to find the solution of 12 = 3v.
Answer:
Tape Diagrams:
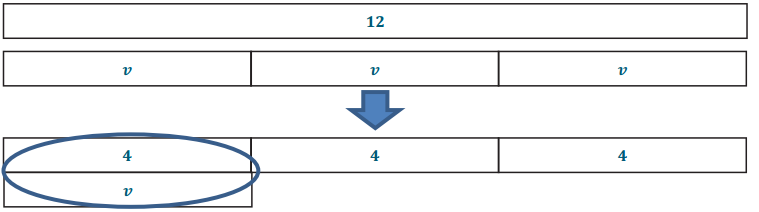
Algebraically:
12 = 3v
12 ÷ 3 = 3v ÷ 3
4 = v
Check:
12 = 3(4); 12 = 12. This number sentence is true, so 4 is the correct solution.