Engage NY Eureka Math 6th Grade Module 3 Lesson 9 Answer Key
Eureka Math Grade 6 Module 3 Lesson 9 Example Answer Key
Example 1.
Interpreting Number Line Models to Compare Numbers
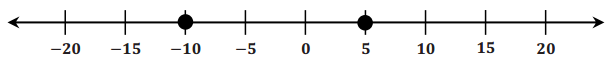
Answer:
Answers may vary. Every August, the Boy Scouts go on an 8-day 40-mile hike. At the halfway point (20 miles into the hike), there is a check-in station for Scouts to check in and register. Thomas and Evan are Scouts in 2 different hiking groups. By Wednesday morning, Evan’s group has 10 miles to go before it reaches the check-in station, and Thomas’s group is 5 miles beyond the station. Zero on the number line represents the check-in station.
Eureka Math Grade 6 Module 3 Lesson 9 Exercise Answer Key
Exercise 1.
Create a real-world situation that relates to the points shown in the number line model. Be sure to describe the relationship between the values of the two points and how it relates to their order on the number line.
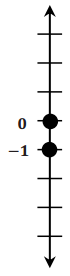
Answer:
Answers will vary.
Alvin lives in Canada and is recording the outside temperature each night before he goes to bed. On Monday night, he recorded a temperature of 0 degrees Celsius. On Tuesday night, he recorded a temperature of – 1 degree Celsius. Tuesday night’s temperature was colder than Monday night’s temperature. – 1 is less than 0, so the associated point is below 0 on a vertical number line.
For each problem, determine if you agree or disagree with the representation. Then, defend your stance by citing specific details in your writing.
Exercise 2.
FelIcia needs to write a story problem that relates to the order In which the numbers – 6 and – 10 are represented on a number line. She writes the following:
“During a recent football game, our team lost yards on two consecutive downs. We lost 6\(\frac{1}{2}\) yards on the first down. During the second down, our quarterback was sacked for an additional 10-yard loss. On the number line, I represented this situation by first locating -6\(\frac{1}{2}\). I located the point by moving 6\(\frac{1}{2}\) units to the left of zero. Then, I graphed the second point by moving 10 units to the left of 0.”
Answer:
Agree. – 10 is less than – 6\(\frac{1}{2}\) since – 10 is to the left of – 6\(\frac{1}{2}\) on the number line. Since both numbers are negative, they indicate the team lost yards on both football plays, but they lost more yards on the second play.
Exercise 3.
Manuel looks at a number line diagram that has the points –\(\frac{3}{4}\) and –\(\frac{1}{2}\) graphed. He writes the following related story:
“I borrowed 50 cents from my friend, Lester. I borrowed 75 cents from my friend, Calvin. I owe Lester less than I owe Calvin.”
Answer:
Agree. – \(\frac{3}{4}\) is equivalent to – 0.75 and – \(\frac{1}{2}\) is equivalent to – 0.50. – 0.50 and – 0.75 both show that he owes money. But – 0.50 is farther to the right on a number line, so Manuel does not owe Lester as much as he owes Calvin.
Exercise 4.
Henry located 2\(\frac{1}{4}\) and 2. 1 on a number line. He wrote the following related story:
“In gym class, both Jerry and I ran for 20 minutes. Jerry ran 2\(\frac{1}{4}\) miles, and 1 ran 2. 1 miles. I ran a farther distance.”
Answer:
Disagree. 2\(\frac{1}{4}\) is greater than 2.1 since 2\(\frac{1}{4}\) is equivalent to 2.25. On the number line, the point associated with 2.25 is to the right of 2. 1. Jerry ran a farther distance.
Exercise 5.
Sam looked at two points that were graphed on a vertical number line. He saw the points – 2 and 1. 5. He wrote the following description:
“I am looking at a vertical number line that shows the location of two specific points. The first point is a negative number, so it is below zero. The second point is a positive number, so it is above zero. The negative number is – 2.
The positive number is \(\frac{1}{2}\) unit more than the negative number.”
Answer:
Disagree. Sam was right when he said the negative number is below zero and the positive number is above zero. But 1.5 is 1\(\frac{3}{4}\) units above zero, and – 2 is 2 units below zero. So, altogether, that means the positive number is 3\(\frac{1}{2}\) units more than – 2.
Exercise 6.
Claire draws a vertical number line diagram and graphs two points: – 10 and 10. She writes the following related story:
“These two locations represent different elevations. One location is 10 feet above sea level, and one location is 10 feet below sea level. On a number line, 10 feet above sea level is represented by graphing a point at 10, and 10 feet below sea level is represented by graphing a point at – 10.”
Answer:
Agree. Zero in this case represents sea level Both locations are 10 feet from zero but in opposite directions, so they are graphed on the number line at 10 and – 10.
Exercise 7.
Mrs. Kimble, the sixth-grade math teacher, asked the class to describe the relationship between two points on the number line, 7.45 and 7. 5, and to create a real-world scenario. Jackson writes the following story:
“Two friends, Jackie and Jennie, each brought money to the fair. Jackie brought more than Jennie. jackie brought $7.45, and Jennie brought $7. 50. Since 7.45 has more digits than 7.5, It would come after 7.5 on the number line, or to the right, so it is a greater value.”
Answer:
Disagree. Jackson is wrong by saying that 7.45 is to the right of 7.5 on the number line. 7. 5 is the same as 7.50, and it is greater than 7.45. When I count by hundredths starting at 7.45, I would say 7.46, 7.47, 7.48, 7.49, and then 7.50. So, 7. 50 is greater than 7.45, and the associated point falls to the right of the point associated with 7.45 on the number line.
Exercise 8.
Justine graphs the points associated with the following numbers on a vertical number line: – 1\(\frac{1}{4}\) – 1\(\frac{1}{2}\), and 1. She then writes the following real-world scenario:
“The nurse measured the height of three sixth-grade students and compared their heights to the height of a typical sixth grader. Two of the students’ heights are below the typical height, and one is above the typical height. The point whose coordinate is 1 represents the student who has a height that is 1 inch above the typical height. Give this information, Justine determined that the student represented by the point associated with – 1\(\frac{1}{4}\) is the shortest of the three students.”
Answer:
Disagree. Justine was wrong when she said the point – 1\(\frac{1}{4}\) represents the shortest of the three students. If zero stands for no change from the typical height, then the point associated with – 1\(\frac{1}{2}\) is farther below zero than the point associated with – 1\(\frac{1}{4}\). The greatest value is positive 1. Positive 1 represents the tallest person. The shortest person is represented by – 1\(\frac{1}{2}\).
Eureka Math Grade 6 Module 3 Lesson 9 Problem Set Answer Key
Write a story related to the points shown in each graph. Be sure to include a statement relating the numbers graphed on the number line to their order.
Question 1.

Answer:
Answers will vary. Marcy earned no bonus points on her first math quiz. She earned 4 bonus points on her second math quiz. Zero represents earning no bonus points, and 4 represents earning 4 bonus points. Zero is graphed to the left of 4 on the number line. Zero is less than 4.
Question 2.
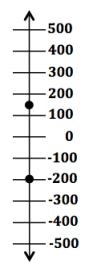
Answer:
Answers will vary. My uncle’s investment lost $200 in May. In June, the investment gained $150. The situation is represented by the points – 200 and 150 on the vertical number line. Negative 200 is below zero, and 150 is above zero. – 200 is less than 150.
Question 3.

Answer:
Answers will vary. I gave my sister $1.50 last week. This week, I gave her $0.50. The points – 1.50 and – 0.50 represent the change to my money supply. We know that – 1.50 is to the left of – 0. 50 on the number line; therefore, – 0. 50 is greater than – 1.50.
Question 4.
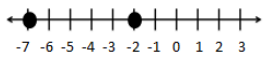
Answer:
Answers will vary. A fish is swimming 7 feet below the water’s surface. A turtle is swimming 2 feet below the water’s surface. We know that – 7 is to the left of – 2 on the number line. This means – 7 is less than – 2.
Question 5.
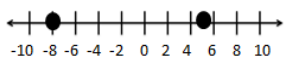
Answer:
Answers will vary. I spent $8 on a CD last month. I earned $5 in allowance last month. – 8 and 5 represent the changes to my money last month. – 8 is to the left of 5 on a number line. – 8 is 3 units farther away from zero than 5, which means that I spent $3 more on the CD than I made in allowance.
Question 6.
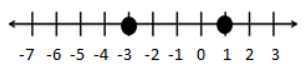
Answer:
Answers will vary. Skip, Mark, and Angelo were standing in line in gym class. Skip was the third person behind
Mark. Angelo was the first person ahead of Mark. If Mark represents zero on the number line, then Skip is associated with the point at -3, and Angelo is associated with the point at 1. 1 is 1 unit to the right of zero, and -3 is 3 units to the left of zero. -3 is less than 1.
Question 7.
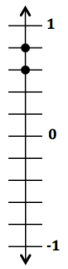
Answer:
Answers will vary. I rode my bike \(\frac{3}{5}\) miles on Saturday and \(\frac{4}{5}\) miles on Sunday. On a vertical number line, \(\frac{3}{5}\) and \(\frac{4}{5}\) are both associated with points above zero, but \(\frac{4}{5}\) is above \(\frac{3}{5}\). This means that \(\frac{4}{5}\) is greater than \(\frac{3}{5}\).
Eureka Math Grade 6 Module 3 Lesson 9 Exit Ticket Answer Key
Question 1.
Interpret the number line diagram shown below, and write a statement about the temperature for Tuesday compared to Monday at 11:00 p.m.

Answer:
At 11:00p.m. on Monday, the temperature was about 40 degrees Fahrenheit, but at 11:00 p.m. on Tuesday, it was – 10 degrees Fahrenheit. Tuesday’s temperature of – 10 degrees is below zero, but 40 degrees is above zero. It was much warmer on Monday at 11:00 p.m. than on Tuesday at that time.
Question 2.
If the temperature at 11:00 p.m. on Wednesday is warmer than Tuesday’s temperature but still below zero, what is a possible value for the temperature at 11:00 p.m. Wednesday?
Answer:
Answers will vary but must be between 0 and – 10. A possible temperature for Wednesday at 11:00 p.m. is – 3 degrees Fahrenheit because – 3 is less than zero and greater than – 10.