Engage NY Eureka Math 6th Grade Module 3 Lesson 7 Answer Key
Eureka Math Grade 6 Module 3 Lesson 7 Example Answer Key
Example 1.
The record low temperatures for a town in Maine are – 20°F for January and – 19°F for February. Order the numbers from least to greatest. Explain how you arrived at the order.
Answer:
→ Read: January: – 20 and February: – 19
→ Draw: Draw a number line model.
→ Write: Since – 20 is farthest below zero and – 19 is above – 20 on the vertical number line, – 20 is less than – 19.
→ Answer: – 20, – 19

Example 2.
Henry, Janon, and Clark are playing a card game. The object of the game Is to finish with the most points. The scores at the end of the game are Henry: – 7, Janon: 0, and Clark: – 5. Who won the game? Who came in last place? Use a number line model, and explain how you arrived at your answer.
Answer:
→ Read: Henry: – 7, fanon: O, and Clark: —5
→ Draw:

→ Explain: – 7, – 5, 0
→ Janon won the game, and Henry came in last place. I ordered the numbers on a number line, and – 7 is farthest to the left. That means – 7 is the smallest of the three numbers, so Henry came in last place. Next on the number line is – 5, which is to the right of – 7 but to the left of 0. Farthest to the right is 0; therefore, 0 is the greatest of the three numbers. This means Janon won the game.
Eureka Math Grade 6 Module 3 Lesson 7 Exercise Answer Key
Exercise 1.
a. Graph the number 7 and its opposite on the number line. Graph the number 5 and its opposite on the number line.
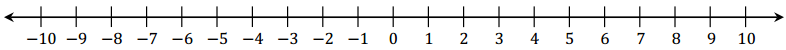
Answer:

b. Where does 7 lie in relation to 5 on the number line?
Answer:
On the number line, 7 is 2 units to the right of 5.
c. Where does the opposite of 7 lie on the number line in relation to the opposite of 5?
Answer:
On the number line, – 7 is 2 units to the left of – 5.
d. I am thinking of two numbers. The first number lies to the right of the second number on a number line. What can you say about the location of their opposites? (If needed, refer to your number line diagram.)
Answer:
On the number line, the opposite of the second number must lie to the right of the opposite of the first number. If we call the first number f and the second number s, then – f and – s will have the opposite order off and s because – f and – s are opposites off and s, so they lie on the opposite side of zero.
For each problem, order the rational numbers from least to greatest by first reading the problem, then drawing a number line diagram, and finally, explaining your answer.
Exercise 2.
Jon’s time for running the mile in gym class is 9.2 minutes. Jacky’s time is 9. 18 minutes. Who ran the mile in less
time?
9.18, 9.2
I drew a number line and graphed 9.2 and 9. 18; 9.2 is to the right of 9. 18. So, 9. 18 is less than 9.2, which means Jacky ran the mile in less time than Jon.
Exercise 3.
Mrs. Rodriguez is a teacher at Westbury Middle School. She gIves bonus points on tests for outstanding written answers and deducts points for answers that are not written correctly. She uses rational numbers to represent the points. She wrote the following on students’ papers: Student A: – 2 points, Student B: – 2. 5 points. Did Student A or Student B perform worse on the test?
Answer:
– 2.5, – 2
I drew a number line, and – 2 and – 2.5 are both to the left of zero, but – 2.5 is to the left of – 2. So, – 2.5 is less than – 2. That means Student B did worse than Student A.
Exercise 4.
A carp is swimming approximately 8\(\frac{1}{4}\) feet beneath the water’s surface, and a sunfish is swimming approximately 3\(\frac{1}{2}\) feet beneath the water’s surface. Which fish is swimming farther beneath the water’s surface?
Answer:
– 8\(\frac{1}{4}\), – 3\(\frac{1}{2}\)
I drew a vertical number line, and – 8\(\frac{1}{4}\) as farther below zero than – 3\(\frac{1}{2}\). So, – 8\(\frac{1}{4}\) as less than – 3\(\frac{1}{2}\) , which means the carp is swimming farther beneath the water’s surface.
For each problem, order the rational numbers from least to greatest by first reading the problem, then drawing a number line diagram, and finally, explaining your answer.
Exercise 5.
Henry, Janon, and Clark are playing another round of the card game. Their scores this time are as follows: Clark: – 1, Janon: – 2, and Henry: – 4. Who won? Who came in last place?
Answer:
– 4, – 2, – 1
Clark won the game, and Henry came in last place. I ordered the numbers on a number line, and —4 is farthest to the left. That means – 4 is the smallest of the three numbers, so Henry lost. Next on the number line is – 2, which is to the right of – 4 and to the left of – 1. Farthest to the right is – 1, which is the greatest of the three negative numbers, so Clark won the game.
Exercise 6.
Represent each of the following elevations using a rational number. Then, order the numbers from least to greatest.
Cayuga Lake 122 meters above sea level
Mount Marcy 1, 629 meters above sea level
New York Stock Exchange Vault 15.24 meters below sea level
Answer:
– 15.24; 122; 1,629
I drew a number line, and – 15.24 is the only number to the left of zero, so it is the least (because as you move to the right, the numbers increase). Next on the number line is 122, which is to the right of zero. Last on the number line is 1,629, which is to the right of 122, so 1,629 meters is the greatest elevation.
Closing: What is the Value of Each Number, and Which is Larger?
Use your teacher’s verbal clues and this number line to determine which number is larger.
Answer:
Eureka Math Grade 6 Module 3 Lesson 7 Problem Set Answer Key
Question 1.
In the table below, list each set of rational numbers in order from least to greatest. Then, list their opposites. Finally, list the opposites in order from least to greatest. The first example has been completed for you.
Answer:
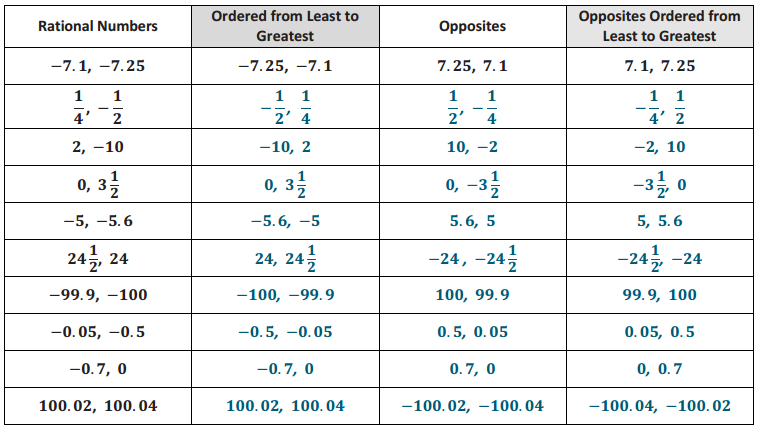
Question 2.
For each row, what pattern do you notice between the numbers in the second and fourth columns? Why is this so?
Answer:
For each row, the numbers in the second and fourth columns are opposites, and their order is opposite. This is because on the number line, as you move to the right, numbers increase. But as you move to the left, the numbers decrease. So, when comparing 5 and 10, 10 is to the right of 5; therefore, 10 is greater than 5. However, – 10 is to the left of – 5; therefore, – 10 is less than – 5.
Eureka Math Grade 6 Module 3 Lesson 7 Exit Ticket Answer Key
Question 1.
In math class, Christina and Brett are debating the relationship between two rational numbers. Read their claims below, and then write an explanation of who is correct. Use a number line model to support your answer.
Christina’s Claim: “I know that 3 is greater than 2\(\frac{1}{2}\). So, – 3 must be greater than – 2\(\frac{1}{2}\).”
Brett’s Claim: “Yes, 3 is greater than 2\(\frac{1}{2}\), but when you look at their opposites, their order will be opposite. So, that means – 2\(\frac{1}{2}\) is greater than – 3.”
Answer:
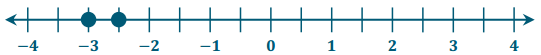
Brett is correct. I graphed the numbers on the number line, and – 3 is to the left of – 2\(\frac{1}{2}\). The numbers increase as you move to the right, so – 2\(\frac{1}{2}\) is greater than – 3.