Engage NY Eureka Math 6th Grade Module 2 Lesson 7 Answer Key
Eureka Math Grade 6 Module 2 Lesson 7 Example Answer Key
Example 1.
Model the following using a partitive interpretation.
\(\frac{3}{4} \div \frac{2}{5}\)
Answer:
\(\frac{2}{5}\) of what number is \(\frac{3}{4}\)?
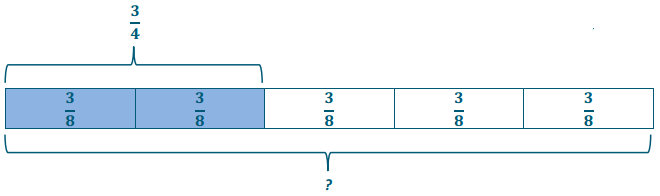
Shade 2 of the 5 sections \(\left(\frac{2}{5}\right)\).
Label the part that is known \(\left(\frac{3}{4}\right)\).
Make notes below on the math sentences needed to solve the problem.
Answer:
→ Let’s relate what we just did to multiplication.
Look back at the model. What was the first thing you did? What was the next thing you did?
We found half of \(\frac{3}{4}\). Then we took the result and multiplied by 5.
→ We can record this process using multiplication:
\(\frac{3}{4} \div \frac{2}{5}=\left(\frac{1}{2} \cdot \frac{3}{4}\right) \cdot 5\)
→ How can you show that \(\left(\frac{1}{2} \cdot \frac{3}{4}\right)\) . 5 is equivalent to \(\frac{3}{4} \cdot \frac{5}{2}\)? What does that tell you about \(\frac{3}{4} \div \frac{2}{5}\) and \(\frac{3}{4} \times \frac{5}{2}\)?
Since we are multiplying, we can rearrange the order of our factors:
\(\frac{1}{2} \cdot \frac{3}{4} \cdot 5=\frac{3}{4} \cdot\left(\frac{1}{2} \cdot 5\right)=\frac{3}{4} \cdot \frac{5}{2}\)
Since \(\frac{3}{4} \div \frac{2}{5}\) is equal to \(\left(\frac{1}{2} \cdot \frac{3}{4}\right)\) . 5, and that’s equal to \(\frac{3}{4} \cdot \frac{5}{2}\), we can say that \(\frac{3}{4} \div \frac{2}{5}=\frac{3}{4} \cdot \frac{5}{2}\).
→ To solve this division problem, we can invert the divisor and multiply. This is called the invert and multiply
method.
Example 2.
Model the following using a measurement interpretation.
\(\frac{3}{5} \div \frac{1}{4}\)
Answer:
\(\frac{3}{5}\) is how many fourths?
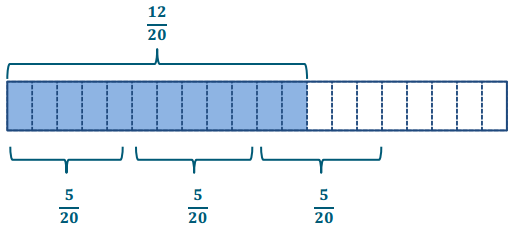
Convert the whole and the divisor to the same fractional units first. Then divide the numerators.
\(\frac{3}{5} \div \frac{1}{4}=\frac{12}{20} \div \frac{5}{20}\) = 12 twentieths ÷ 5 twentieths \(\frac{12}{5}=2 \frac{2}{5}\)
Example 3.
\(\frac{2}{3} \div \frac{3}{4}\)
Answer:
Answer may vary.
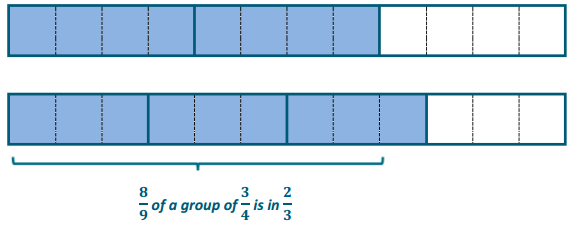
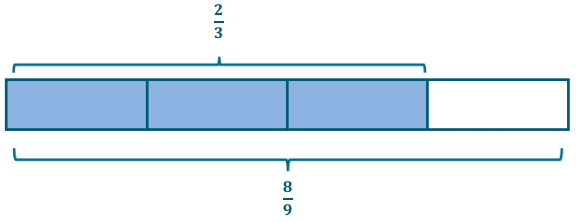
Show the number sentences below.
Answer:
\(\frac{2}{3} \div \frac{3}{4}=\frac{8}{12} \div \frac{9}{12}=\frac{8}{9}\)
\(\frac{1}{3} \cdot \frac{2}{3} \cdot 4=\frac{8}{9}\)
\(\frac{2}{3} \div \frac{3}{4}=\frac{2}{3} \cdot \frac{4}{3}=\frac{8}{9}\)
Eureka Math Grade 6 Module 2 Lesson 7 Problem Set Answer Key
Invert and multiply to divide.
Question 1.
a. \(\frac{2}{3} \div \frac{1}{4}\)
Answer:
= \(\frac{2}{3} \times \frac{4}{1}=\frac{8}{3}\)
b. \(\frac{2}{3}\) ÷ 4
Answer:
= \(\frac{2}{3} \times \frac{1}{4}=\frac{1}{6}\)
c. 4 ÷ \(\frac{2}{3}\)
Answer:
= 4 × \(\frac{3}{2}\) = 6
Question 2.
a. \(\frac{1}{3} \div \frac{1}{4}\)
Answer:
= \(\frac{1}{3} \times \frac{4}{1}=\frac{4}{3}\)
b. \(\frac{1}{8} \div \frac{3}{4}\)
Answer:
= \(\frac{1}{8} \times \frac{4}{3}=\frac{1}{6}\)
c. \(\frac{9}{4} \div \frac{6}{5}\)
Answer:
= \(\frac{9}{4} \times \frac{5}{6}=\frac{15}{8}\)
Question 3.
a. \(\frac{2}{3} \div \frac{3}{4}\)
Answer:
= \(\frac{2}{3} \times \frac{4}{3}=\frac{8}{9}\)
b. \(\frac{3}{5} \div \frac{3}{2}\)
Answer:
= \(\frac{3}{5} \times \frac{2}{3}=\frac{2}{5}\)
c. \(\frac{22}{4} \div \frac{2}{5}\)
Answer:
= \(\frac{22}{4} \times \frac{5}{2}=\frac{55}{4}\)
Question 4.
Summer used \(\frac{2}{5}\) of her ground beef to make burgers. If she used \(\frac{3}{4}\) pounds of beef, how much beef did she have at first?
Answer:
\(\frac{3}{4}\) is \(\frac{2}{5}\) of what? So, \(\frac{3}{4} \div \frac{2}{5}=\frac{3}{4} \times \frac{5}{2}=\frac{15}{8}=1 \frac{7}{8}\)
Question 5.
Alistair has 5 half-pound chocolate bars. It takes 1\(\frac{1}{2}\) pounds of chocolate, broken into chunks, to make a batch of cookies. How many batches can Alistair make with the chocolate he has on hand?
Answer:
\(1 \frac{1}{2}=\frac{3}{2}\)
\(\frac{5}{2}\) is how many \(\frac{3}{2}\)
\(\frac{5}{2} \div \frac{3}{2}=\frac{5}{2} \times \frac{2}{3}=\frac{5}{3}\)
Alistair can only make 1 full batch, but he has enough to make another \(\frac{2}{3}\) batch.
Question 6.
Draw a model that shows \(\frac{2}{5} \div \frac{1}{3}\). Find the answer as well.
Answer:
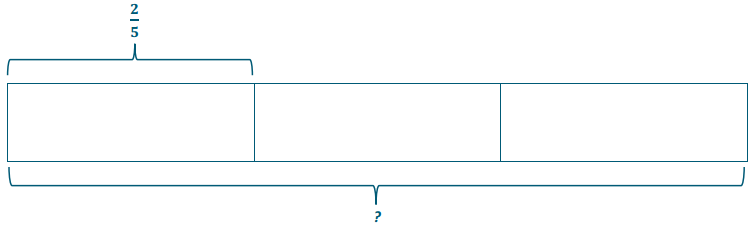
\(\frac{2}{5} \div \frac{1}{3}=\frac{2}{5} \cdot \frac{3}{1}=\frac{6}{5}\) or 1\(\frac{1}{5}\)
Question 7.
Draw a model that shows \(\frac{3}{4} \div \frac{1}{2}\). Find the answer as well.
Answer:
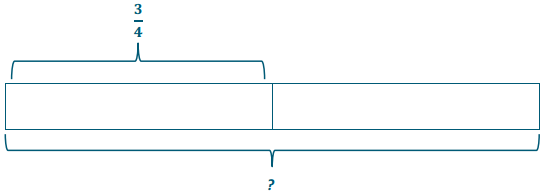
\(\frac{3}{4} \div \frac{1}{2}=\frac{3}{4} \cdot \frac{2}{1}=\frac{6}{4}\) or 1\(\frac{1}{2}\)
Eureka Math Grade 6 Module 2 Lesson 7 Exit Ticket Answer Key
Question 1.
Write the reciprocal of the following numbers.

Answer:

Question 2.
Rewrite this division expression as an equivalent multiplication expression: \(\frac{5}{8} \div \frac{2}{3}\)
Answer:
\(\frac{5}{8} \cdot \frac{3}{2} \text { or } \frac{1}{2} \cdot \frac{5}{8} \cdot 3\)
Question 3.
Solve problem 2. Draw a model to support your solution.
Answer:
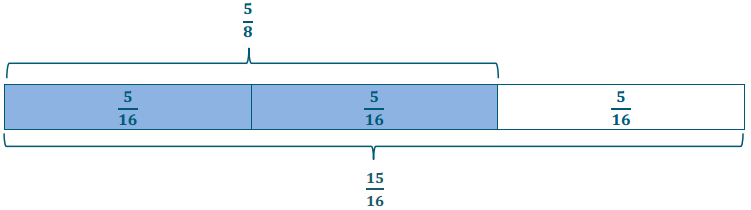
\(\frac{5}{8} \div \frac{2}{3}=\frac{5}{8} \cdot \frac{3}{2}=\frac{15}{16}\)