Engage NY Eureka Math 5th Grade Module 6 Lesson 18 Answer Key
Eureka Math Grade 5 Module 6 Lesson 18 Problem Set Answer Key
Question 1.
Use the plane to the right to complete the following tasks.
a. Draw a line t whose rule is y is always 0.7.
b. Plot the points from Table A on the grid in order. Then, draw line segments to connect the points.
|
(x, y) |
| (0.1, 0.5) |
| (0.2, 0.3) |
| (0.3, 0.5) |
| (0.5, 0.1) |
| (0.6, 0.2) |
| (0.8, 0.2) |
| (0.9, 0.1) |
| (1.1, 0.5) |
| (1.2, 0.3) |
| (1.3, 0.5) |
|
(x, y) |
c. Complete the drawing to create a figure that is symmetric about line t. For each point in Table A, record the corresponding point on the other side of the line of symmetry in Table B.
d. Compare the y-coordinates in Table A with those in Table B. What do you notice?
e. Compare the x-coordinates in Table A with those in Table B. What do you notice?
Answer:
C. The Table B is written below
|
(x, y) |
| (0.1, 0.9 ) |
| (0.2 , 1.1) |
| (0.3, 0.9) |
| (0.5, 1.3) |
| (‘0.6, 1.2) |
| (0.8, 1.2) |
| (0.9, 1.3) |
| (1.1, 0.9) |
| (1.2, 1.1) |
| (1.3, 0.9) |
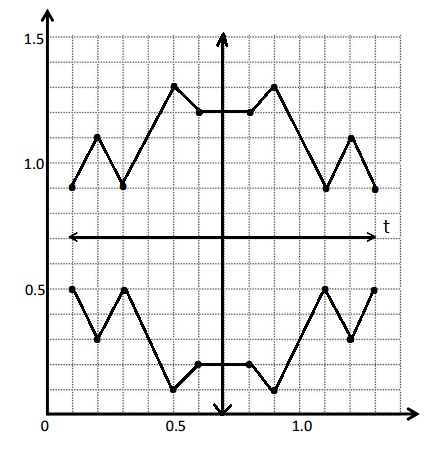
d . The differences in the Table A is same as the difference in the Table B .
e. The X-coordinates in the table A is same as the in the Table B.
Question 2.
This figure has a second line of symmetry. Draw the line on the plane, and write the rule for this line.
Answer:
The X is always the 0.7 is the rule used for second symmetry of line .
Question 3.
Use the plane below to complete the following tasks.
a. Draw a line u whose rule is y is equal to x + \(\frac{1}{4}\).
b. Construct a figure with a total of 6 points, all on the same side of the line.
c. Record the coordinates of each point, in the order in which they were drawn, in Table A.
d. Swap your paper with a neighbor, and have her complete parts (e–f), below.
|
(x, y) |
|
(x, y) |
e. Complete the drawing to create a figure that is symmetric about u. For each point in Table A, record the corresponding point on the other side of the line of symmetry in Table B.
f. Explain how you found the points symmetric to your partner’s about u.
Answer:
a. Line u is drawn
c. Points of Table A .
|
(x, y) |
| (\(\frac{1}{4}\) , \(\frac{3}{4}\) ) |
| (\(\frac{2}{4}\) , 2) |
| (1\(\frac{1}{4}\), 2) |
| (1\(\frac{1}{4}\), 2\(\frac{2}{4}\)) |
| ( 1 \(\frac{3}{4}\), 2\(\frac{3}{4}\)) |
| ( 2, 2\(\frac{3}{4}\)) |
d. Points of Table B
|
(x, y) |
| (\(\frac{2}{4}\), \(\frac{2}{4}\)) |
| ( 1\(\frac{3}{4}\), \(\frac{3}{4}\) ) |
| (1 \(\frac{3}{4}\) , 1 \(\frac{2}{4}\) ) |
| ( 2\(\frac{1}{4}\), 1\(\frac{2}{4}\) ) |
| ( 2\(\frac{3}{4}\), 2) |
| ( 2\(\frac{2}{4}\), 2\(\frac{1}{4}\) ) |
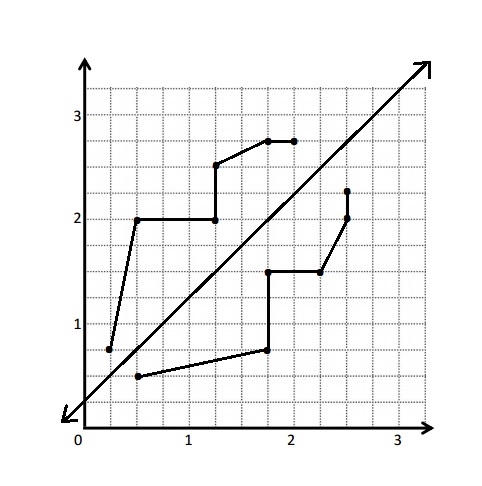
f. Using the line of symmetry i counted the units . The units should be equal distance from the line of u . Points are marked carefully because rule used here is y is equal to x + \(\frac{1}{4}\) .
Eureka Math Grade 5 Module 6 Lesson 18 Exit Ticket Answer Key
Kenny plotted the following pairs of points and said they made a symmetric figure about a line with the rule:
y is always 4.
(3, 2) and (3, 6)
(4, 3) and (5, 5)
(5, \(\frac{3}{4}\)) and (5, 7\(\frac{1}{4}\))
(7, 1\(\frac{1}{2}\)) and (7, 6\(\frac{1}{2}\))
Is his figure symmetrical about the line? How do you know?
Answer:
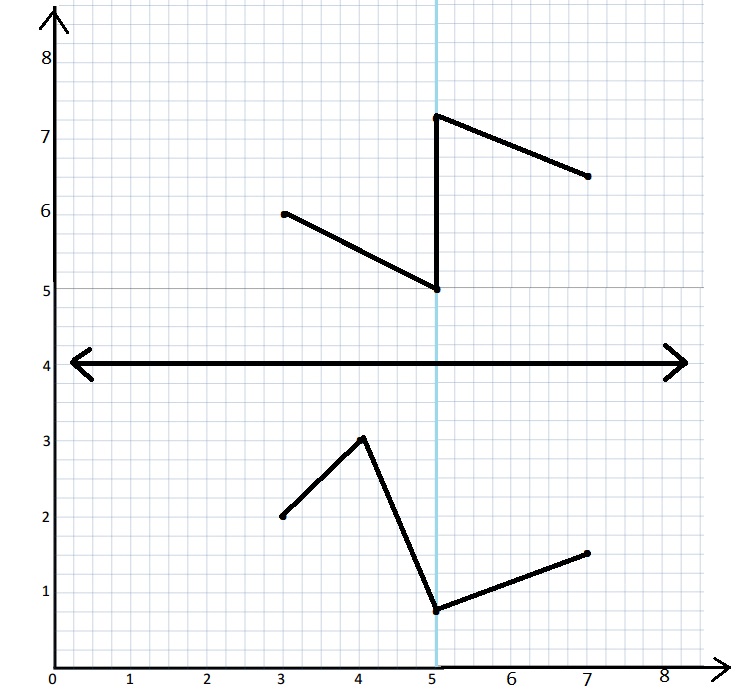
No,
Explanation :
The units should be equal distance from the line of . But the point (4, 3) and (5,5) have different lengths from the line .
so, the image formed is not symmetric figure .
Eureka Math Grade 5 Module 6 Lesson 18 Homework Answer Key
Question 1.
Use the plane to the right to complete the following tasks.
a. Draw a line s whose rule is x is always 5.
b. Plot the points from Table A on the grid in order. Then, draw line segments to connect the points in order.
|
(x, y) |
| (1, 13) |
| (1, 12) |
| (2, 10) |
| (4, 9) |
| (4, 3) |
| (1, 2) |
| (5, 2) |
|
(x, y) |
c. Complete the drawing to create a figure that is symmetric about line s. For each point in Table A, record the symmetric point on the other side of s.
d. Compare the y-coordinates in Table A with those in Table B. What do you notice?
e. Compare the x-coordinates in Table A with those in Table B. What do you notice?
Answer:
c. The points of Table B are
|
(x, y) |
| (9, 13) |
| (9, 12) |
| (8, 10) |
| (6, 9) |
| (6, 3) |
| (9, 2) |
| (5, 2) |
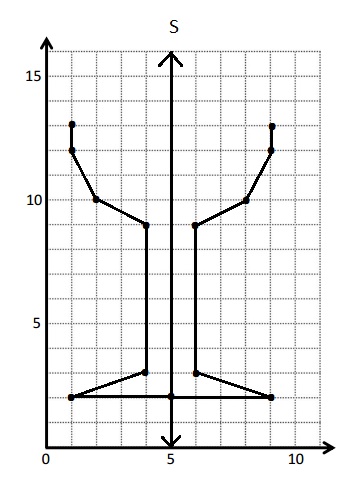
d. The Y-coordinates in Table A and Table B are equal .
e. The x-coordinates in Table A with those in Table B are in reverse order like 1-9 , 2-8,3-7, 4-6 and 5-5 numbers are interchanged with respective number .
Question 2.
Use the plane to the right to complete the following tasks.
a. Draw a line p whose rule is, y is equal to x.
b. Plot the points from Table A on the grid in order. Then, draw line segments to connect the points.
|
(x, y) |
| (\(\frac{1}{2}\), \(\frac{1}{2}\)) |
| (1, 2) |
| (1\(\frac{1}{2}\), 1\(\frac{1}{2}\)) |
| (2, 4) |
| (3\(\frac{1}{2}\), 3\(\frac{1}{2}\)) |
| (4, 4\(\frac{1}{2}\)) |
| (5, 5) |
|
(x, y) |
c. Complete the drawing to create a figure that is symmetric about line p. For each point in Table A, record the symmetric point on the other side of the line p in Table B.
d. Compare the y-coordinates in Table A with those in Table B. What do you notice?
e. Compare the x-coordinates in Table A with those in Table B. What do you notice?
Answer:
c. The points of Table B.
|
(x, y) |
| (\(\frac{1}{2}\), \(\frac{1}{2}\)) |
| (2, 1) |
| (1\(\frac{1}{2}\), 1\(\frac{1}{2}\)) |
| (4, 2) |
| (3\(\frac{1}{2}\), 3\(\frac{1}{2}\)) |
| (4\(\frac{1}{2}\), 4) |
| (5, 5) |