Engage NY Eureka Math 5th Grade Module 4 Lesson 8 Answer Key
Eureka Math Grade 5 Module 4 Lesson 8 Problem Set Answer Key
Question 1.
Laura and Sean find the product of \(\frac{2}{3}\) × 4 using different methods.
Laura: It’s 2 thirds of 4.
\(\frac{2}{3}\) × 4 = \(\frac{4}{3}\) + \(\frac{4}{3}\) = 2 × \(\frac{4}{3}\) = \(\frac{8}{3}\)
Sean: It’s 4 groups of 2 thirds.
\(\frac{2}{3}\) + \(\frac{2}{3}\) + \(\frac{2}{3}\) + \(\frac{2}{3}\) = 4 × \(\frac{2}{3}\) = \(\frac{8}{3}\)
Use words, pictures, or numbers to compare their methods in the space below.
Answer:
Laura:
2/3 * 4 = 4/3 + 4/3 = 2*4/3 = 8/3
Sean:
2/3 + 2/3 + 2/3 + 2/3 = 4 * 2/3 = 8/3
Both methods are correct. 2/3 *4 is 2 thirds of 4, and it will also have the same product as the 4 groups of 2 thirds.
Question 2.
Rewrite the following addition expressions as fractions as shown in the example.
Example: \(\frac{2}{3}\) + \(\frac{2}{3}\) + \(\frac{2}{3}\) + \(\frac{2}{3}\) = (\(\frac{4 × 2}{3}\)) = \(\frac{8}{3}\)
a. \(\frac{7}{4}\) + \(\frac{7}{4}\) + \(\frac{7}{4}\) =
Answer:
21/4
Explanation:
The addition expression for the fraction given is :
7/4 + 7/4 + 7/4 = (3 × 7)/4 = 21/4
b. \(\frac{14}{5}\) + \(\frac{14}{5}\) =
Answer:
28/5
Explanation:
The addition expression for the fraction given is :
14/5 + 14/5 = (2×14)/5 = 28/5
c. \(\frac{4}{7}\) + \(\frac{4}{7}\) + \(\frac{4}{7}\) =
Answer:
12/7
Explanation:
4/7 +4/7 +4/7 = (3×4)/7 = 12/7
Question 3.
Solve and model each problem as a fraction of a set and as repeated addition.
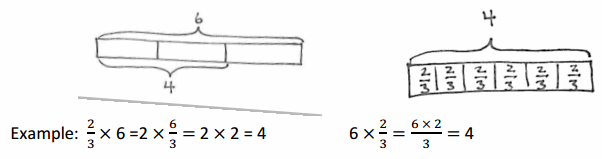
a. \(\frac{1}{2}\) × 8 8 × \(\frac{1}{2}\)
Answer:
1 ×8/2 = 1×4 = 4
8 × 1/2 = (8×1)/2
= 8/2
= 4
b. \(\frac{3}{5}\) × 10 10 × \(\frac{3}{5}\)
Answer:
6
Explanation:
3 ×10/5 = 3 × 2 = 6
10 × 3/5 = (10×3)/5 = 30/5 = 6
Question 4.
Solve each problem in two different ways as modeled in the example.
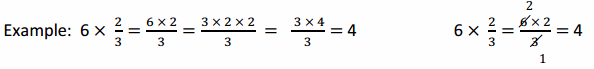
a. 14 × \(\frac{3}{7}\) 14 × \(\frac{3}{7}\)
Answer:
6
Explanation:
(14×3)/7 = (7×2×3)/7 = (7×6)/7 = 6
(14 × 3)/7 = (2×3)/1 = 6
b. \(\frac{3}{4}\) × 36 \(\frac{3}{4}\) ×36
Answer:
27
Explanation:
(3×36)/4 = (3×4×9)/4 = (4×27)/4 = 27
(3×36)/4 = (3×9) = (3×9) = 27
c. 30 × \(\frac{13}{10}\) 30 × \(\frac{13}{10}\)
Answer:
39
Explanation:
(30×13)/10 = (10×3×13)/10 = (10×39)/10 = 39
(30 ×13)/10 = (3×13)/1 = 39
d. \(\frac{9}{8}\) ×32 \(\frac{9}{8}\) × 32
Answer:
36
Explanation:
(9×32)/8 = (9×4×8)/8 = (36×8)/8 = 36
(9×32)/8 = (9×32)/8 = (9×4)/1 = 36
Question 5.
Solve each problem any way you choose.
a. \(\frac{1}{2}\) × 60 \(\frac{1}{2}\) minute = __________ seconds
Answer:
30seconds
Explanation:
The answer and the procedure are explained clearly in the below steps.
1 minute = 60 seconds
(1×60)/2 = (1×30)/1 = 30
b. \(\frac{3}{4}\) × 60 \(\frac{3}{4}\) hour = __________ minutes
Answer:
45 minutes
Explanation:
The answer and the procedure are explained clearly in the below steps.
1 hour = 60 minutes
(3×60)/4 = (3×15)/1 = 45
c. \(\frac{3}{10}\) × 1,000 \(\frac{3}{10}\) kilogram = __________ grams”
Answer:
300 grams
Explanation:
The answer and the procedure are explained clearly in the below steps.
1 kilogram = 1000 grams
(3×1000)/1 = 300
d. \(\frac{4}{5}\) × 100 \(\frac{4}{5}\) meter = __________ centimeters
Answer:
80 centimeters
Explanation:
The answer and the procedure are explained clearly in the below steps.
1 meter
(4×100)/5 = (4×20)/1 = 80
Eureka Math Grade 5 Module 4 Lesson 8 Exit Ticket Answer Key
Solve each problem in two different ways as modeled in the example.
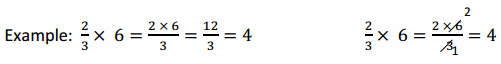
a. \(\frac{2}{3}\) × 15 \(\frac{2}{3}\) × 15
Answer:
10
Explanation:
By solving the given question in two methods we could get the same answer i.e 10. The Explanation is given below.
2/3 × 15 = (2 ×15)/3 = 30/3 = 10
2/3 ×15 = (2×15)/3 = (2×5) = 10
b. \(\frac{5}{4}\) × 12 \(\frac{5}{4}\) × 12
Answer:
15
Explanation:
By solving the given question in two methods we could get the same answer i.e 15. The process for the question is done below.
5/4 × 12 = (5×12)/4 = (60)/4 =15
5/4 ×12 = ( 5×12)/4 = (5×3) =15
Eureka Math Grade 5 Module 4 Lesson 8 Homework Answer Key
Question 1.
Rewrite the following expressions as shown in the example.
Example: \(\frac{2}{3}\) + \(\frac{2}{3}\) + \(\frac{2}{3}\) + \(\frac{2}{3}\) = (\(\frac{4 × 2}{3}\)) = \(\frac{8}{3}\)
a. \(\frac{5}{3}\) + \(\frac{5}{3}\) + \(\frac{5}{3}\)
Answer:
5
Explanation:
(\(\frac{3 × 5}{3}\)) = \(\frac{15}{3}\) =5
b. \(\frac{13}{5}\) + \(\frac{13}{5}\)
Answer:
\(\frac{26}{5}\)
Explanation:
(\(\frac{2 × 13}{5}\)) = \(\frac{26}{5}\)
c. \(\frac{9}{4}\) + \(\frac{9}{4}\) + \(\frac{9}{4}\)
Answer:
\(\frac{27}{4}\)
Expalanation:
(\(\frac{3 × 9}{4}\)) = \(\frac{27}{4}\)
Question 2.
Solve each problem in two different ways as modeled in the example.
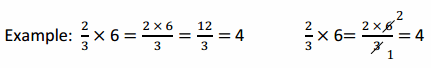
a. \(\frac{3}{4}\) × 16 \(\frac{3}{4}\) × 16
Answer:
12
Explanation:
(\(\frac{3 × 16}{4}\)) = \(\frac{48}{4}\) = 12
(\(\frac{3 × 16}{4}\)) = \(\frac{3 × 4}{1}\) = 12
b. \(\frac{4}{3}\) × 12 \(\frac{4}{3}\) × 12
Answer:
16
Explanation:
(\(\frac{4 × 12}{3}\)) = \(\frac{48}{3}\) = 16
(\(\frac{4 × 12}{3}\)) = \(\frac{4 × 12}{1}\) = 16
c. 40 × \(\frac{11}{10}\) 40 × \(\frac{11}{10}\)
Answer:
44
Explanation:
(\(\frac{40 × 11}{10}\)) = \(\frac{440}{10}\) = 44
(\(\frac{40× 11}{10}\)) = \(\frac{4 × 11}{1}\) = \(\frac{44}{1}\) = 44
d. \(\frac{7}{6}\) × 36 \(\frac{7}{6}\)× 36
Answer:
42
Explanation:
(\(\frac{7 × 36}{6}\)) = \(\frac{252}{6}\) = 42
(\(\frac{7 × 36}{6}\)) = \(\frac{7 × 6}{1}\) = 42
e. 24 × \(\frac{5}{8}\) 24 × \(\frac{5}{8}\)
Answer:
15
Explanation:
(\(\frac{24 × 5}{8}\)) = \(\frac{126}{8}\) = 15
(\(\frac{24 × 5}{8}\)) = \(\frac{3 × 5}{1}\) = 15
f. 18 × \(\frac{5}{12}\) 18 × \(\frac{5}{12}\)
Answer:
7 1/2
Explanation:
(\(\frac{18 × 5}{12}\)) = \(\frac{90}{12}\) = 7 6/12 = 7 1/2
(\(\frac{18 × 5}{12}\)) = \(\frac{3 × 5 }{2}\) = \(\frac{15}{2}\)= 7 1/2
g. \(\frac{10}{9}\) × 21 \(\frac{10}{9}\) × 21
Answer:
23 3/9 = 23 1/3
Explanation:
(\(\frac{10 × 21}{9}\)) = \(\frac{210}{9}\) = 23 3/9 = 23 1/3
(\(\frac{10 × 21}{9}\)) = \(\frac{10 × 7}{3}\) = \(\frac{70}{3}\) = 23 1/3
Question 3.
Solve each problem any way you choose.
a. \(\frac{1}{3}\) × 60 \(\frac{1}{3}\) minute = _________ seconds
Answer:
20 seconds
Explanation:
(\(\frac{1 × 60}{3}\)) = \(\frac{60}{3\) = 20
b. \(\frac{4}{5}\) × 60 \(\frac{4}{5}\) hour = _________ minutes
Answer:
48 minutes
Explanation:
(\(\frac{4 × 60}{5}\)) = \(\frac{48}{1\) = 48
c. \(\frac{7}{10}\) × 1000 \(\frac{7}{10}\) kilogram = _________ grams
Answer:
700 grams
Explanation:
(\(\frac{7 × 1000}{10}\)) = \(\frac{700}{1\) = 700
d. \(\frac{3}{5}\)× 100 \(\frac{3}{5}\) meter = _________ centimeters
Answer:
60 centimeres
Explanation:
(\(\frac{3 × 100}{5}\)) = \(\frac{60}{1\) = 60