Engage NY Eureka Math 5th Grade Module 4 Lesson 26 Answer Key
Eureka Math Grade 5 Module 4 Lesson 26 Problem Set Answer Key
Question 1.
Draw a model or tape diagram to solve. Use the thought bubble to show your thinking. Write your quotient in the blank. Use the example to help you.
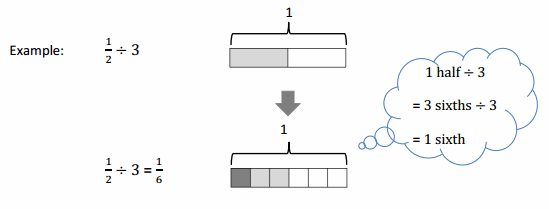
a. \(\frac{1}{3}\) ÷ 2 = __________
Answer:
\(\frac{1}{3}\) ÷ 2 = \(\frac{1}{6}\).
Explanation:
Given that \(\frac{1}{3}\) ÷ 2.
1 third ÷ 2
= 2 sixth ÷ 2
= 1 sixth.
So \(\frac{1}{3}\) ÷ 2 = \(\frac{1}{6}\).
b. \(\frac{1}{3}\) ÷ 4 = __________
Answer:
\(\frac{1}{3}\) ÷ 4 = \(\frac{1}{12}\).
Explanation:
Given that \(\frac{1}{3}\) ÷ 4.
1 third ÷ 4
= 4 twelths ÷ 4
= 1 twelfth.
So \(\frac{1}{3}\) ÷ 4 = \(\frac{1}{12}\).
c. \(\frac{1}{4}\) ÷ 2 = __________
Answer:
\(\frac{1}{4}\) ÷ 2 = \(\frac{1}{8}\).
Explanation:
Given that \(\frac{1}{4}\) ÷ 2.
1 fourth ÷ 2
= 2 eighths ÷ 2
= 1 eighth.
So \(\frac{1}{4}\) ÷ 2 = \(\frac{1}{8}\).
d. \(\frac{1}{4}\) ÷ 3 = __________
Answer:
\(\frac{1}{4}\) ÷ 3 = \(\frac{1}{12}\).
Explanation:
Given that \(\frac{1}{4}\) ÷ 3.
1 fourth ÷ 3
= 3 twelfths ÷ 3
= 1 twelfth.
So \(\frac{1}{3}\) ÷ 2 = \(\frac{1}{6}\).
Question 2.
Divide. Then, multiply to check.
a. \(\frac{1}{2}\) ÷ 7
Answer:
\(\frac{1}{2}\) ÷ 7 = 14.
Explanation:
Given that \(\frac{1}{2}\) ÷ 7 which is 14. Now we need to check, so
\(\frac{1}{14}\) × 7 which is \(\frac{1}{2}\).
b. \(\frac{1}{3}\) ÷ 6
Answer:
\(\frac{1}{3}\) ÷ 6 = 18.
Explanation:
Given that \(\frac{1}{3}\) ÷ 6 which is 18. Now we need to check, so
\(\frac{1}{18}\) × 6 which is \(\frac{1}{3}\).
c. \(\frac{1}{4}\)÷ 5
Answer:
\(\frac{1}{4}\) ÷ 5 = 20.
Explanation:
Given that \(\frac{1}{4}\) ÷ 5 which is 20. Now we need to check, so
\(\frac{1}{20}\) × 5 which is \(\frac{1}{4}\).
d. \(\frac{1}{5}\) ÷ 4
Answer:
\(\frac{1}{5}\) ÷ 4 = 20.
Explanation:
Given that \(\frac{1}{5}\) ÷ 4 which is 20. Now we need to check, so
\(\frac{1}{20}\) × 4 which is \(\frac{1}{5}\).
e. \(\frac{1}{5}\) ÷ 2
Answer:
\(\frac{1}{5}\) ÷ 2 = 10.
Explanation:
Given that \(\frac{1}{5}\) ÷ 2 which is 10. Now we need to check, so
\(\frac{1}{10}\) × 2 which is \(\frac{1}{5}\).
f. \(\frac{1}{6}\) ÷ 3
Answer:
\(\frac{1}{6}\) ÷ 3 = 18.
Explanation:
Given that \(\frac{1}{6}\) ÷ 3 which is 18. Now we need to check, so
\(\frac{1}{18}\) × 3 which is \(\frac{1}{6}\).
g. \(\frac{1}{8}\) ÷ 2
Answer:
\(\frac{1}{8}\) ÷ 2 = 16.
Explanation:
Given that \(\frac{1}{8}\) ÷ 2 which is 16. Now we need to check, so
\(\frac{1}{16}\) × 2 which is \(\frac{1}{16}\).
h. \(\frac{1}{10}\) ÷ 10
Answer:
\(\frac{1}{10}\) ÷ 10 = 100.
Explanation:
Given that \(\frac{1}{10}\) ÷ 10 which is 1. Now we need to check, so
\(\frac{1}{100}\) × 10 which is \(\frac{1}{10}\).
Question 3.
Tasha eats half her snack and gives the other half to her two best friends for them to share equally. What portion of the whole snack does each friend get? Draw a picture to support your response.
Answer:
Each friend gets \(\frac{1}{4}\) of the snack.
Explanation:
Given that Tasha eats half her snack and gives the other half to her two best friends for them to share equally, so the portion of the whole snack does each friend get is
\(\frac{1}{2}\) ÷ 2 = 1 half ÷ 2
= 2 fourths ÷ 2
= 1 fourth.
So each friend gets \(\frac{1}{4}\) of the snack.
Question 4.
Mrs. Appler used \(\frac{1}{2}\) gallon of olive oil to make 8 identical batches of salad dressing.
a. How many gallons of olive oil did she use in each batch of salad dressing?
Answer:
\(\frac{1}{16}\) gal olive oil in each batch.
Explanation:
Given that a gallons of olive oil did she use in each batch of salad dressing, so
\(\frac{1}{2}\) ÷ 8 = \(\frac{8}{16}\) ÷ 8
= 8 sixteenth ÷ 8
= \(\frac{1}{16}\) gal olive oil in each batch.
b. How many cups of olive oil did she use in each batch of salad dressing?
Answer:
She uses 1 cup of olive in each batch of salad dressing.
Explanation:
The number of cups of olive oil did she use in each batch of salad dressing is
1 gallon = 16 cups and \(\frac{1}{16}\) = 1 cups, so she uses 1 cup of olive in each batch of salad dressing.
Question 5.
Mariano delivers newspapers. He always puts \(\frac{3}{4}\) of his weekly earnings in his savings account and then divides the rest equally into 3 piggy banks for spending at the snack shop, the arcade, and the subway.
a. What fraction of his earnings does Mariano put into each piggy bank?
Answer:
Mariano puts \(\frac{1}{12}\) of his earnings in each piggy bank.
Explanation:
Given that Mariano delivers newspapers and puts \(\frac{3}{4}\) of his weekly earnings in his savings account and then divides the rest equally into 3 piggy banks for spending at the snack shop, the arcade, and the subway. So the fraction of his earnings that Mariano put into each piggy bank is
\(\frac{1}{4}\) ÷ 3 = 1 fourth ÷ 3
= 3 twelfths ÷ 3
= 1 twelfth.
So Mariano puts \(\frac{1}{12}\) of his earnings in each piggy bank.
b. If Mariano adds $2.40 to each piggy bank every week, how much does Mariano earn per week delivering papers?
Answer:
Mariano earns per week delivering papers is $7.20 × 4 which is $28.8.
Explanation:
Given that Mariano adds $2.40 to each piggy bank every week which is $2.40 × 3 = $7.20 , so Mariano earn per week delivering papers is $7.20 × 4 which is $28.8.
Eureka Math Grade 5 Module 4 Lesson 26 Exit Ticket Answer Key
Question 1.
Solve. Support at least one of your answers with a model or tape diagram.
a. \(\frac{1}{2}\) ÷ 4 = ______
Answer:
\(\frac{1}{2}\) ÷ 4 = \(\frac{1}{8}\).
Explanation:
Given that \(\frac{1}{2}\) ÷ 4.
1 second ÷ 2
= 2 eights ÷ 2
= 1 eights.
So \(\frac{1}{2}\) ÷ 4 = \(\frac{1}{8}\).
b. \(\frac{1}{8}\) ÷ 5 = ______
Answer:
\(\frac{1}{8}\) ÷ 5 = \(\frac{1}{40}\).
Explanation:
Given that \(\frac{1}{8}\) ÷ 5.
1 eight ÷ 5
= 5 forty ÷ 5
= 1 forty.
So \(\frac{1}{8}\) ÷ 5 = \(\frac{1}{40}\).
Question 2.
Larry spends half of his workday teaching piano lessons. If he sees 6 students, each for the same amount of time, what fraction of his workday is spent with each student?
Answer:
The fraction of his workday is spent with each student is \(\frac{1}{12}\).
Explanation:
Given that Larry spends half of his workday teaching piano lessons. And the duration of piano lessons is \(\frac{1}{2}\). As he sees 6 students, each for the same amount of time. So,
the duration of teaching each student = duration of teaching piano lessons ÷ Number of students.
= \(\frac{1}{2}\) ÷ 6
= \(\frac{1}{2}\) × 6
= \(\frac{1}{12}\).
So the fraction of his workday is spent with each student is \(\frac{1}{12}\).
Eureka Math Grade 5 Module 4 Lesson 26 Homework Answer Key
Question 1.
Solve and support your answer with a model or tape diagram. Write your quotient in the blank.
a. \(\frac{1}{2}\) ÷ 4 = ______
Answer:
\(\frac{1}{2}\) ÷ 4 = \(\frac{1}{8}\).
Explanation:
Given that \(\frac{1}{2}\) ÷ 4.
1 second ÷ 2
= 2 eights ÷ 2
= 1 eight.
So \(\frac{1}{2}\) ÷ 4 = \(\frac{1}{8}\).
b. \(\frac{1}{3}\) ÷ 6 = ______
Answer:
\(\frac{1}{3}\) ÷ 6 = \(\frac{1}{18}\).
Explanation:
Given that \(\frac{1}{3}\) ÷ 6.
1 third ÷ 6
= 6 eighteens ÷ 6
= 1 eighteen.
So \(\frac{1}{3}\) ÷ 6 = \(\frac{1}{18}\).
c. \(\frac{1}{4}\)÷ 3 = ______
Answer:
\(\frac{1}{4}\) ÷ 3 = \(\frac{1}{12}\).
Explanation:
Given that \(\frac{1}{4}\) ÷ 3.
1 fourth ÷ 3
= 3 twelfths ÷ 3
= 1 twelfths.
So \(\frac{1}{4}\) ÷ 3 = \(\frac{1}{12}\).
d. \(\frac{1}{5}\) ÷ 2 = ______
Answer:
\(\frac{1}{5}\) ÷ 2 = \(\frac{1}{10}\).
Explanation:
Given that \(\frac{1}{5}\) ÷ 2.
1 fifth ÷ 2
= 2 tens ÷ 2
= 1 ten.
So \(\frac{1}{5}\) ÷ 2 = \(\frac{1}{10}\).
Question 2.
Divide. Then, multiply to check.
a. \(\frac{1}{2}\) ÷ 10
Answer:
\(\frac{1}{2}\) ÷ 10 = 20.
Explanation:
Given that \(\frac{1}{2}\) ÷ 10 which is 20. Now we need to check, so
\(\frac{1}{20}\) × 10 which is \(\frac{1}{2}\).
b. \(\frac{1}{4}\) ÷ 10
Answer:
\(\frac{1}{4}\) ÷ 10 = 40.
Explanation:
Given that \(\frac{1}{4}\) ÷ 10 which is 40. Now we need to check, so
\(\frac{1}{40}\) × 10 which is \(\frac{1}{4}\).
c. \(\frac{1}{3}\)÷ 5
Answer:
\(\frac{1}{3}\) ÷ 5 = 15.
Explanation:
Given that \(\frac{1}{3}\) ÷ 5 which is 15. Now we need to check, so
\(\frac{1}{15}\) × 5 which is \(\frac{1}{3}\).
d. \(\frac{1}{5}\) ÷ 3
Answer:
\(\frac{1}{5}\) ÷ 3 = 15.
Explanation:
Given that \(\frac{1}{5}\) ÷ 3 which is 15. Now we need to check, so
\(\frac{1}{15}\) × 3 which is \(\frac{1}{15}\).
e. \(\frac{1}{8}\) ÷ 4
Answer:
\(\frac{1}{8}\) ÷ 4 = 32.
Explanation:
Given that \(\frac{1}{8}\) ÷ 4 which is 32. Now we need to check, so
\(\frac{1}{32}\) × 4 which is \(\frac{1}{8}\).
f. \(\frac{1}{7}\) ÷ 3
Answer:
\(\frac{1}{7}\) ÷ 3 = 21.
Explanation:
Given that \(\frac{1}{7}\) ÷ 3 which is 21. Now we need to check, so
\(\frac{1}{21}\) × 3 which is \(\frac{1}{7}\).
g. \(\frac{1}{10}\) ÷ 5
Answer:
\(\frac{1}{10}\) ÷ 5 = 50.
Explanation:
Given that \(\frac{1}{10}\) ÷ 5 which is 50. Now we need to check, so
\(\frac{1}{50}\) × 5 which is \(\frac{1}{10}\).
h. \(\frac{1}{5}\) ÷ 20
Answer:
\(\frac{1}{5}\) ÷ 20 = 100.
Explanation:
Given that \(\frac{1}{5}\) ÷ 20 which is 100. Now we need to check, so
\(\frac{1}{100}\) × 20 which is \(\frac{1}{5}\).
Question 3.
Teams of four are competing in a quarter-mile relay race. Each runner must run the same exact distance. What is the distance each teammate runs?
Answer:
Each person will run \(\frac{1}{16}\) miles.
Explanation:
Given that there are teams of four are competing in a quarter-mile relay race and each runner must run the same exact distance, so the distance each teammate runs is,
so each person will run = the total distance ÷ number of persons in a team
= \(\frac{1}{4}\) ÷ 4
= \(\frac{1}{4}\) × \(\frac{1}{4}\)
= \(\frac{1}{16}\).
so each person will run \(\frac{1}{16}\) miles.
Question 4.
Solomon has read \(\frac{1}{3}\) of his book. He finishes the book by reading the same amount each night for 5 nights.
a. What fraction of the book does he read each of the 5 nights?
Answer:
Solomon reads \(\frac{2}{15}\) of the book each night.
Explanation:
Given that Solomon has read \(\frac{1}{3}\) of his book, so 1 – \(\frac{1}{3}\) which is \(\frac{2}{3}\) of the book is left to be read. And we have that, in 5 nights Solomon reads \(\frac{2}{3}\) of the book. So for 1 night he will read \(\frac{2}{3}\) × \(\frac{1}{5}\) which is \(\frac{2}{15}\) of the book.
b. If he reads 14 pages on each of the 5 nights, how long is the book?
Answer:
The total number of pages in the book is 105.
Explanation:
Let the total number of books be X, as he reads 14 pages on each of the 1 night. So he reads 14 × 5 which is 70 pages in 5 nights. So \(\frac{2}{3}\)of the total pages is 70, which is
\(\frac{2}{3}\) X = 70, on solving we will get
X = 105.
So the total number of pages in the book is 105.