Engage NY Eureka Math 5th Grade Module 3 Lesson 15 Answer Key
Eureka Math Grade 5 Module 3 Lesson 15 Sprint Answer Key
A
Circle the Smaller Fraction
Question 1.
\(\frac{1}{2}\) \(\frac{1}{4}\)
Answer:
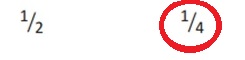
Question 2.
\(\frac{1}{2}\) \(\frac{3}{4}\)
Answer:

Question 3.
\(\frac{1}{2}\) \(\frac{5}{8}\)
Answer:

Question 4.
\(\frac{1}{2}\) \(\frac{7}{8}\)
Answer:
![]()
Question 5.
\(\frac{1}{2}\) \(\frac{1}{10}\)
Answer:

Question 6.
\(\frac{1}{2}\) \(\frac{3}{10}\)
Answer:

Question 7.
\(\frac{1}{2}\) \(\frac{5}{12}\)
Answer:
![]()
Question 8.
\(\frac{1}{2}\) \(\frac{11}{12}\)
Answer:
![]()
Question 9.
\(\frac{1}{2}\) \(\frac{7}{10}\)
Answer:

Question 10.
\(\frac{1}{5}\) \(\frac{9}{10}\)
Answer:
![]()
Question 11.
\(\frac{2}{5}\) \(\frac{1}{10}\)
Answer:
![]()
Question 12.
\(\frac{2}{5}\) \(\frac{3}{10}\)
Answer:

Question 13.
\(\frac{3}{5}\) \(\frac{3}{10}\)
Answer:
![]()
Question 14.
\(\frac{3}{5}\) \(\frac{7}{10}\)
Answer:

Question 15.
\(\frac{4}{5}\) \(\frac{1}{10}\)
Answer:

Question 16.
\(\frac{4}{5}\) \(\frac{9}{10}\)
Answer:

Question 17.
\(\frac{1}{3}\) \(\frac{1}{9}\)
Answer:
![]()
Question 18.
\(\frac{1}{3}\) \(\frac{2}{9}\)
Answer:

Question 19.
\(\frac{1}{3}\) \(\frac{4}{9}\)
Answer:

Question 20.
\(\frac{1}{3}\) \(\frac{8}{9}\)
Answer:

Question 21.
\(\frac{1}{3}\) \(\frac{1}{12}\)
Answer:

Question 22.
\(\frac{1}{3}\) \(\frac{5}{12}\)
Answer:

Question 23.
\(\frac{1}{4}\) \(\frac{1}{8}\)
Answer:

Question 24.
\(\frac{1}{4}\) \(\frac{3}{8}\)
Answer:

Question 25.
\(\frac{1}{4}\) \(\frac{7}{12}\)
Answer:

Question 26.
\(\frac{1}{4}\) \(\frac{11}{12}\)
Answer:

Question 27.
\(\frac{1}{6}\) \(\frac{7}{12}\)
Answer:

Question 28.
\(\frac{1}{6}\) \(\frac{11}{12}\)
Answer:
![]()
Question 29.
\(\frac{2}{3}\) \(\frac{1}{6}\)
Answer:
![]()
Question 30.
\(\frac{2}{3}\) \(\frac{5}{6}\)
Answer:
![]()
Question 31.
\(\frac{2}{3}\) \(\frac{2}{9}\)
Answer:
![]()
Question 32.
\(\frac{2}{3}\) \(\frac{4}{9}\)
Answer:

Question 33.
\(\frac{2}{3}\) \(\frac{1}{12}\)
Answer:

Question 34.
\(\frac{2}{3}\) \(\frac{5}{12}\)
Answer:
![]()
Question 35.
\(\frac{2}{3}\) \(\frac{11}{12}\)
Answer:
![]()
Question 36.
\(\frac{2}{3}\) \(\frac{7}{12}\)
Answer:
![]()
Question 37.
\(\frac{3}{4}\) \(\frac{1}{8}\)
Answer:
![]()
Question 38.
\(\frac{3}{4}\) \(\frac{1}{8}\)
Answer:
![]()
Question 39.
\(\frac{5}{6}\) \(\frac{7}{12}\)
Answer:
![]()
Question 40.
\(\frac{5}{6}\) \(\frac{5}{12}\)
Answer:
![]()
Question 41.
\(\frac{6}{7}\) \(\frac{38}{42}\)
Answer:
![]()
Question 42.
\(\frac{7}{8}\) \(\frac{62}{72}\)
Answer:
![]()
Question 43.
\(\frac{49}{54}\) \(\frac{8}{9}\)
Answer:
![]()
Question 44.
\(\frac{67}{72}\) \(\frac{11}{12}\)
Answer:
![]()
B
Circle the Smaller Fraction
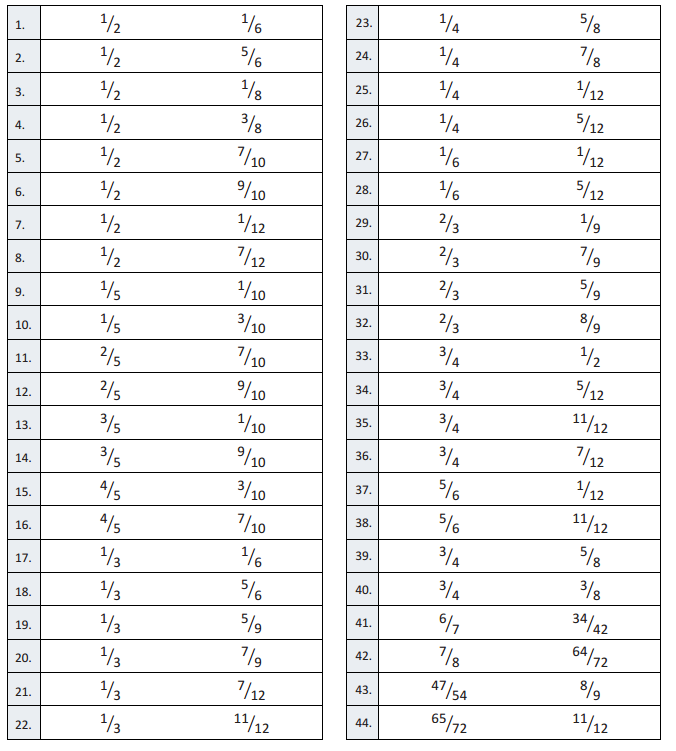
Question 1.
\(\frac{1}{2}\) \(\frac{1}{6}\)
Answer:

Question 2.
\(\frac{1}{2}\) \(\frac{5}{6}\)
Answer:

Question 3.
\(\frac{1}{2}\) \(\frac{1}{8}\)
Answer:

Question 4.
\(\frac{1}{2}\) \(\frac{3}{8}\)
Answer:

Question 5.
\(\frac{1}{2}\) \(\frac{7}{10}\)
Answer:

Question 6.
\(\frac{1}{2}\) \(\frac{9}{10}\)
Answer:

Question 7.
\(\frac{1}{2}\) \(\frac{1}{12}\)
Answer:

Question 8.
\(\frac{1}{2}\) \(\frac{7}{12}\)
Answer:

Question 9.
\(\frac{1}{5}\) \(\frac{1}{10}\)
Answer:

Question 10.
\(\frac{1}{5}\) \(\frac{3}{10}\)
Answer:

Question 11.
\(\frac{2}{5}\) \(\frac{1}{10}\)
Answer:

Question 12.
\(\frac{2}{5}\) \(\frac{9}{10}\)
Answer:
![]()
Question 13.
\(\frac{3}{5}\) \(\frac{1}{10}\)
Answer:

Question 14.
\(\frac{3}{5}\) \(\frac{9}{10}\)
Answer:
![]()
Question 15.
\(\frac{4}{5}\) \(\frac{3}{10}\)
Answer:

Question 16.
\(\frac{4}{5}\) \(\frac{7}{10}\)
Answer:

Question 17.
\(\frac{1}{3}\) \(\frac{1}{6}\)
Answer:

Question 18.
\(\frac{1}{3}\) \(\frac{5}{6}\)
Answer:

Question 19.
\(\frac{1}{3}\) \(\frac{5}{9}\)
Answer:
![]()
Question 20.
\(\frac{1}{3}\) \(\frac{7}{9}\)
Answer:

Question 21.
\(\frac{1}{3}\) \(\frac{7}{12}\)
Answer:

Question 22.
\(\frac{1}{3}\) \(\frac{11}{12}\)
Answer:

Question 23.
\(\frac{1}{4}\) \(\frac{5}{8}\)
Answer:

Question 24.
\(\frac{1}{4}\) \(\frac{7}{8}\)
Answer:

Question 25.
\(\frac{1}{4}\) \(\frac{1}{12}\)
Answer:

Question 26.
\(\frac{1}{4}\) \(\frac{5}{12}\)
Answer:

Question 27.
\(\frac{1}{6}\) \(\frac{1}{12}\)
Answer:

Question 28.
\(\frac{1}{6}\) \(\frac{5}{12}\)
Answer:

Question 29.
\(\frac{2}{3}\) \(\frac{1}{9}\)
Answer:

Question 30.
\(\frac{2}{3}\) \(\frac{7}{9}\)
Answer:

Question 31.
\(\frac{2}{3}\) \(\frac{5}{9}\)
Answer:

Question 32.
\(\frac{2}{3}\) \(\frac{8}{9}\)
Answer:
![]()
Question 33.
\(\frac{2}{3}\) \(\frac{1}{12}\)
Answer:
![]()
Question 34.
\(\frac{3}{4}\) \(\frac{1}{2}\)
Answer:
![]()
Question 35.
\(\frac{3}{4}\) \(\frac{5}{12}\)
Answer:
![]()
Question 36.
\(\frac{3}{4}\) \(\frac{7}{12}\)
Answer:

Question 37.
\(\frac{5}{6}\) \(\frac{1}{12}\)
Answer:
![]()
Question 38.
\(\frac{5}{6}\) \(\frac{11}{12}\)
Answer:

Question 39.
\(\frac{3}{4}\) \(\frac{5}{8}\)
Answer:
![]()
Question 40.
\(\frac{3}{4}\) \(\frac{3}{8}\)
Answer:
![]()
Question 41.
\(\frac{6}{7}\) \(\frac{34}{42}\)
Answer:

Question 42.
\(\frac{7}{8}\) \(\frac{64}{72}\)
Answer:
![]()
Question 43.
\(\frac{47}{54}\) \(\frac{8}{9}\)
Answer:

Question 44.
\(\frac{65}{72}\) \(\frac{11}{12}\)
Answer:

Eureka Math Grade 5 Module 3 Lesson 15 Problem Set Answer Key
Solve the word problems using the RDW strategy. Show all of your work.
Question 1.
In a race, the-second place finisher crossed the finish line 1\(\frac{1}{3}\) minutes after the winner. The third-place finisher was 1\(\frac{3}{4}\) minutes behind the second-place finisher. The third-place finisher took 34\(\frac{2}{3}\) minutes. How long did the winner take?
Answer:
Fraction of time of Second place finisher crossed the line after = 1\(\frac{1}{3}\) minutes = \(\frac{4}{3}\)
Fraction of time of Third place finisher is behind the second place = 1\(\frac{3}{4}\) minutes = \(\frac{7}{4}\)
Fraction of time the third place finisher took = 34\(\frac{2}{3}\) = \(\frac{105}{3}\)
Fraction of time the second place runner took = \(\frac{105}{3}\) – \(\frac{7}{4}\) = \(\frac{420}{12}\) – \(\frac{21}{12}\) = \(\frac{399}{12}\) = \(\frac{133}{4}\)
Fraction of time the First place runner took = \(\frac{133}{4}\) – \(\frac{4}{3}\) = \(\frac{399}{12}\) – \(\frac{16}{12}\) = \(\frac{383}{12}\) = 31 \(\frac{11}{12}\) .
Therefore the First Runner took = 31 \(\frac{11}{12}\) .minutes.
Question 2.
John used 1\(\frac{3}{4}\) kg of salt to melt the ice on his sidewalk. He then used another 3\(\frac{4}{5}\) kg on the driveway. If he originally bought 10 kg of salt, how much does he have left?
Answer:
Fraction of Salt used by John =1\(\frac{3}{4}\) kg = \(\frac{7}{4}\) kg
Fraction of Salt used again =3\(\frac{4}{5}\) kg = \(\frac{24}{5}\) kg
Fraction of salt used = \(\frac{7}{4}\) + \(\frac{24}{5}\) = \(\frac{35}{20}\) + \(\frac{96}{20}\) = \(\frac{131}{20}\) = 6 \(\frac{11}{20}\) .
Total Salt = 10 kg.
Fraction of salt left = 10 – \(\frac{131}{20}\) = \(\frac{200}{20}\) – \(\frac{131}{20}\) = \(\frac{69}{20}\) = 3\(\frac{9}{20}\) .
Therefore Fraction of salt left = 3\(\frac{9}{20}\) .
Question 3.
Sinister Stan stole 3\(\frac{3}{4}\) oz of slime from Messy Molly, but his evil plans require 6\(\frac{3}{8}\) oz of slime. He stole another 2\(\frac{3}{5}\) oz of slime from Rude Ralph. How much more slime does Sinister Stan need for his evil plan?
Answer:
Fraction of slime stolen from Messy Molly = 3\(\frac{3}{4}\) = \(\frac{15}{4}\) oz
Fraction of slime stolen from Messy Molly again = 2\(\frac{3}{5}\) = \(\frac{13}{5}\) oz
Total Fraction Stolen = \(\frac{15}{4}\) + \(\frac{13}{5}\) = \(\frac{75}{20}\) + \(\frac{52}{20}\) = \(\frac{127}{20}\) = 6\(\frac{7}{20}\) .
Fraction of more slime required = 6\(\frac{3}{8}\) – \(\frac{127}{20}\) = \(\frac{51}{8}\) – \(\frac{127}{20}\) = \(\frac{255}{40}\) – \(\frac{254}{40}\) = \(\frac{1}{40}\) .
Therefore, Fraction of more slime required = \(\frac{1}{40}\) oz.
Question 4.
Gavin had 20 minutes to do a three-problem quiz. He spent 9\(\frac{3}{4}\) minutes on Problem 1 and 3\(\frac{4}{5}\) minutes on Problem 2. How much time did he have left for Problem 3? Write the answer in minutes and seconds.
Answer:
Time given for 3 problems = 20 minutes
Fraction of time Spent on Problem 1 = 9\(\frac{3}{4}\) minutes = \(\frac{39}{4}\) .
Fraction of Time spent on Problem 2 = 3\(\frac{4}{5}\) = \(\frac{19}{5}\) .
Fraction of Time spent on Problem 3 = x
20 = \(\frac{39}{4}\) + \(\frac{19}{5}\) + x
x = 20 – \(\frac{39}{4}\) – \(\frac{19}{5}\)
x = \(\frac{400}{20}\) – \(\frac{195}{20}\) – \(\frac{76}{20}\)
x = \(\frac{129}{20}\) = 6\(\frac{9}{20}\) .
Therefore, Fraction of Time spent on Problem 3 = 6\(\frac{9}{20}\) .
Question 5.
Matt wants to shave 2\(\frac{1}{2}\) minutes off his 5K race time. After a month of hard training, he managed to lower his overall time from 21\(\frac{1}{5}\) minutes to 19\(\frac{1}{4}\) minutes. By how many more minutes does Matt need to lower his race time?
Answer:
Fraction of Time lowered = 21\(\frac{1}{5}\) minutes to 19\(\frac{1}{4}\) minutes. = \(\frac{106}{5}\) – \(\frac{77}{4}\) = \(\frac{424}{20}\) – \(\frac{385}{20}\) = \(\frac{39}{20}\) =1\(\frac{19}{20}\) .
Fraction of Time shaved = 2\(\frac{1}{2}\) =\(\frac{5}{2}\) .
Fraction of More Time Matt need to lower his race time = \(\frac{5}{2}\) – \(\frac{39}{20}\) = \(\frac{50}{20}\) – \(\frac{39}{20}\) = \(\frac{11}{20}\) = \(\frac{33}{60}\) = 33 minutes .
Eureka Math Grade 5 Module 3 Lesson 15 Exit Ticket Answer Key
Solve the word problem using the RDW strategy. Show all of your work.
Cheryl bought a sandwich for 5\(\frac{1}{2}\) dollars and a drink for $2.60. If she paid for her meal with a $10 bill, how much money did she have left? Write your answer as a fraction and in dollars and cents.
Answer:
Fraction of Cost of sandwich = 5\(\frac{1}{2}\) = \(\frac{11}{2}\) dollar = 5.5 dollar
Fraction of Cost of Drink = $2.60.
Total Cost = 5.5 +2.60 = 8.1 $.
Amount paid = 10$.
Money left = 10 – 8.1 = 1.9 $ .
Eureka Math Grade 5 Module 3 Lesson 15 Homework Answer Key
Solve the word problems using the RDW strategy. Show all of your work.
Question 1.
A baker buys a 5 lb bag of sugar. She uses 1\(\frac{2}{3}\) lb to make some muffins and 2\(\frac{3}{4}\) lb to make a cake. How much sugar does she have left?
Answer:
Total Quantity of Sugar = 5 lb
Fraction of Quantity of Suagr used for muffins = 1\(\frac{2}{3}\) lb = \(\frac{5}{3}\)
Fraction of Quantity of Suagr used cake = 2\(\frac{3}{4}\) lb = \(\frac{11}{4}\)
Fraction of Quantity of Sugar used = \(\frac{5}{3}\) + \(\frac{11}{4}\) = \(\frac{20}{12}\) + \(\frac{33}{12}\) = \(\frac{53}{12}\)
Fraction of Quantity of Sugar left = 5 – \(\frac{53}{12}\) = \(\frac{60}{12}\) – \(\frac{53}{12}\) =\(\frac{7}{12}\) .
Therefore, Fraction of Quantity of sugar left = \(\frac{7}{12}\) .
Question 2.
A boxer needs to lose 3\(\frac{1}{2}\) kg in a month to be able to compete as a flyweight. In three weeks, he lowers his weight from 55.5 kg to 53.8 kg. How many kilograms must the boxer lose in the final week to be able to compete as a flyweight?
Answer:
Fraction of weight need to lose in month = 3\(\frac{1}{2}\) = \(\frac{7}{2}\) = 3.5 kg
Weight lost in 3 weeks = 55.5 – 53.8 = 1.7 kg
Weight need to lose in final week = 3.5 – 1.7 = 1.8 kg.
Question 3.
A construction company builds a new rail line from Town A to Town B. They complete 1\(\frac{1}{4}\) miles in their first week of work and 1\(\frac{2}{3}\) miles in the second week. If they still have 25\(\frac{3}{4}\) miles left to build, what is the distance from Town A to Town B?
Answer:
Fraction of work completed in first week = 1\(\frac{1}{4}\) miles = \(\frac{5}{4}\)
Fraction of work completed in second week = 1\(\frac{2}{3}\) miles = \(\frac{5}{3}\)
Fraction of work left to built = 25\(\frac{3}{4}\) miles = \(\frac{103}{4}\)
Fraction of Distance from Town A to Town B = \(\frac{103}{4}\) + \(\frac{5}{4}\) + \(\frac{5}{3}\) = \(\frac{108}{4}\) + \(\frac{5}{3}\) = \(\frac{324}{12}\) + \(\frac{20}{12}\) = \(\frac{344}{12}\)= 28\(\frac{2}{3}\) .
Therefore, Fraction of Distance from Town A to Town B = 28\(\frac{2}{3}\) miles.
Question 4.
A catering company needs 8.75 lb of shrimp for a small party. They buy 3\(\frac{2}{3}\) lb of jumbo shrimp, 2\(\frac{5}{8}\) lb of medium-sized shrimp, and some mini-shrimp. How many pounds of mini-shrimp do they buy?
Answer:
Quantity of shrimp needed = 8.75 lb =8\(\frac{3}{4}\) = \(\frac{27}{4}\)
Quantity of jumbo shrimp = 3\(\frac{2}{3}\) lb = \(\frac{11}{3}\)
Quantity of medium – sized shrimp = 2\(\frac{5}{8}\) lb = \(\frac{21}{8}\)
Quantity of mini shrimp = x
\(\frac{35}{4}\) = \(\frac{11}{3}\) + \(\frac{21}{8}\) + x
x = \(\frac{210}{24}\) – \(\frac{88}{24}\) – \(\frac{63}{24}\)
x = \(\frac{59}{24}\) = 2 \(\frac{11}{24}\)
Therefore, Quantity of mini shrimp = x = 2 \(\frac{11}{24}\) lb .
Question 5.
Mark breaks up a 9-hour drive into 3 segments. He drives 2\(\frac{1}{2}\) hours before stopping for lunch. After driving some more, he stops for gas. If the second segment of his drive was 1\(\frac{2}{3}\) hours longer than the first segment, how long did he drive after stopping for gas?
Answer:
Total time of the drive = 9 hours .
Fraction of Time drived for first segment = 2\(\frac{1}{2}\) hours = \(\frac{5}{2}\)
Fraction of Time of second segment = 1\(\frac{2}{3}\) hours longer than the first segment = \(\frac{5}{3}\) + \(\frac{5}{2}\) = \(\frac{10}{6}\) + \(\frac{15}{6}\) = \(\frac{25}{6}\) =4\(\frac{1}{6}\)
Fraction of Time of first and second segment= \(\frac{5}{2}\) + \(\frac{25}{6}\) = \(\frac{15}{6}\) + \(\frac{25}{6}\) = \(\frac{40}{6}\) = 6\(\frac{4}{6}\)
Fraction of Time he drive after stopping gas = 9 – \(\frac{40}{6}\) = \(\frac{54}{6}\) – \(\frac{40}{6}\) = \(\frac{14}{6}\) = 2\(\frac{2}{6}\) .
Therefore, Fraction of Time he drive after stopping gas = third segment = 2\(\frac{2}{6}\) hours .