Engage NY Eureka Math 5th Grade Module 3 Lesson 13 Answer Key
Eureka Math Grade 5 Module 3 Lesson 13 Problem Set Answer Key
Question 1.
Are the following expressions greater than or less than 1? Circle the correct answer.
a. \(\frac{1}{2}\) + \(\frac{2}{7}\) greater than 1 less than 1
b. \(\frac{5}{8}\) + \(\frac{3}{5}\) greater than 1 less than 1
c. 1\(\frac{1}{4}\) – \(\frac{1}{3}\) greater than 1 less than 1
d. 3\(\frac{5}{8}\) – 2\(\frac{5}{9}\) greater than1 less than 1
Answer:

Explanation :
a. \(\frac{1}{2}\) + \(\frac{2}{7}\) =
Lcm of 2 and 7 are 14 .
\(\frac{7}{14}\) + \(\frac{4}{14}\) = \(\frac{11}{14}\)
b. \(\frac{5}{8}\) + \(\frac{3}{5}\)
lcm of 8 and 5 is 40.
\(\frac{25}{40}\) + \(\frac{24}{40}\) = \(\frac{49}{40}\) = 1\(\frac{9}{40}\)
c. 1\(\frac{1}{4}\) – \(\frac{1}{3}\) = \(\frac{5}{4}\) – \(\frac{1}{3}\)
lcm of 4 and 3 is 12.
\(\frac{15}{12}\) – \(\frac{4}{12}\) = \(\frac{11}{12}\)
d. 3\(\frac{5}{8}\) – 2\(\frac{5}{9}\) = \(\frac{29}{8}\) – \(\frac{23}{9}\)
lcm of 8 and 9 is 72 .
\(\frac{261}{72}\) – \(\frac{184}{72}\) = \(\frac{77}{72}\) = 1\(\frac{5}{72}\) .
Question 2.
Are the following expressions greater than or less than \(\frac{1}{2}\) ? Circle the correct answer.
a. \(\frac{1}{4}\) + \(\frac{2}{3}\) greater than \(\frac{1}{2}\) less than \(\frac{1}{2}\)
b.\(\frac{3}{7}\) – \(\frac{1}{8}\) greater than \(\frac{1}{2}\) less than \(\frac{1}{2}\)
c. 1\(\frac{1}{7}\) – \(\frac{7}{8}\) greater than \(\frac{1}{2}\) less than \(\frac{1}{2}\)
d. \(\frac{3}{7}\) + \(\frac{2}{6}\) greater than \(\frac{1}{2}\) less than \(\frac{1}{2}\)
Answer:

Explanation :
a. \(\frac{1}{4}\) + \(\frac{2}{3}\)
lcm of 4 and 3 is 12 .
\(\frac{3}{12}\) + \(\frac{8}{12}\) = \(\frac{11}{12}\) greater than \(\frac{1}{2}\)
b.\(\frac{3}{7}\) – \(\frac{1}{8}\)
lcm of 7 and 8 is 56.
\(\frac{24}{56}\) – \(\frac{7}{56}\) = \(\frac{17}{56}\) less than \(\frac{1}{2}\)
c. 1\(\frac{1}{7}\) – \(\frac{7}{8}\) = \(\frac{8}{7}\) – \(\frac{7}{8}\)
lcm of 7 and 8 is 56.
\(\frac{64}{56}\) – \(\frac{49}{56}\) = \(\frac{15}{56}\) less than \(\frac{1}{2}\)
d. \(\frac{3}{7}\) + \(\frac{2}{6}\)
lcm of 7 and 6 is 42.
\(\frac{18}{42}\) + \(\frac{14}{42}\) = \(\frac{32}{42}\) = \(\frac{16}{21}\) greater than \(\frac{1}{2}\) .
Question 3.
Use > , < , or = to make the following statements true.
a. 5\(\frac{2}{3}\) + 3\(\frac{3}{4}\) _______ 8\(\frac{2}{3}\)
b. 4\(\frac{5}{8}\) – 3\(\frac{2}{5}\) _______ 1\(\frac{5}{8}\) + \(\frac{2}{5}\)
c. 5\(\frac{1}{2}\) + 1\(\frac{3}{7}\) _______ 6 + \(\frac{13}{14}\)
d. 15\(\frac{4}{7}\) – 11\(\frac{2}{5}\) _______ 4\(\frac{4}{7}\) + \(\frac{2}{5}\)
Answer:
a. 5\(\frac{2}{3}\) + 3\(\frac{3}{4}\) = 8\(\frac{2}{3}\)
b. 4\(\frac{5}{8}\) – 3\(\frac{2}{5}\) < 1\(\frac{5}{8}\) + \(\frac{2}{5}\)
c. 5\(\frac{1}{2}\) + 1\(\frac{3}{7}\) = 6 + \(\frac{13}{14}\)
d. 15\(\frac{4}{7}\) – 11\(\frac{2}{5}\) > 4\(\frac{4}{7}\) + \(\frac{2}{5}\)
Explanation :
a. 5\(\frac{2}{3}\) + 3\(\frac{3}{4}\) = \(\frac{17}{3}\) + \(\frac{12}{4}\)
lcm of 3 and 4 is 12.
\(\frac{68}{12}\) + \(\frac{36}{12}\) = \(\frac{104}{12}\) = \(\frac{26}{3}\) =8\(\frac{2}{3}
\)
b. 4\(\frac{5}{8}\) – 3\(\frac{2}{5}\) = \(\frac{37}{8}\) – \(\frac{17}{5}\)
lcm of 8 and 5 is 40 .
\(\frac{185}{40}\) – \(\frac{136}{40}\) = \(\frac{49}{40}\) =1\(\frac{9}{40}\)
1\(\frac{5}{8}\) + \(\frac{2}{5}\) = \(\frac{13}{8}\) + \(\frac{2}{5}\)
lcm of 8 and 5 is 40 .
\(\frac{65}{40}\) + \(\frac{16}{5}\) = \(\frac{81}{40}\) = 2\(\frac{1}{40}\)
c. 5\(\frac{1}{2}\) + 1\(\frac{3}{7}\) = \(\frac{11}{2}\) + \(\frac{10}{7}\)
lcm of 2 and 7 is 14.
\(\frac{77}{14}\) + \(\frac{20}{14}\) = \(\frac{97}{14}\) = 6 \(\frac{13}{14}\)
6 + \(\frac{13}{14}\) =\(\frac{84}{14}\) + \(\frac{13}{14}\) = \(\frac{97}{14}\) = 6 \(\frac{13}{14}\)
d. 15\(\frac{4}{7}\) – 11\(\frac{2}{5}\) =\(\frac{109}{7}\) – \(\frac{57}{5}\)
lcm of 7 and 5 is 35 .
\(\frac{545}{35}\) – \(\frac{399}{35}\) = \(\frac{944}{35}\) = 26\(\frac{34}{35}\) .
4\(\frac{4}{7}\) + \(\frac{2}{5}\) = \(\frac{32}{7}\) + \(\frac{2}{5}\)
lcm of 7 and 5 is 35 .
\(\frac{160}{35}\) + \(\frac{14}{35}\) = \(\frac{174}{35}\)= 4\(\frac{34}{35}\)
Question 4.
Is it true that 4\(\frac{3}{5}\) – 3\(\frac{2}{3}\) = 1 + \(\frac{3}{5}\) + \(\frac{2}{3}\)? Prove your answer.
Answer:
No it is wrong
4\(\frac{3}{5}\) – 3\(\frac{2}{3}\) < 1 + \(\frac{3}{5}\) + \(\frac{2}{3}\)
Explanation :
4\(\frac{3}{5}\) – 3\(\frac{2}{3}\) = \(\frac{23}{5}\) – \(\frac{11}{3}\)
lcm of 5 and 3 is 15 .
\(\frac{69}{15}\) – \(\frac{55}{15}\) = \(\frac{14}{15}\)
1 + \(\frac{3}{5}\) + \(\frac{2}{3}\)
lcm of 5 and 3 is 15 .
\(\frac{15}{15}\) + \(\frac{9}{15}\) + \(\frac{10}{15}\) = latex]\frac{34}{15}[/latex] = 2latex]\frac{4}{15}[/latex] .
Question 5.
Jackson needs to be 1\(\frac{3}{4}\) inches taller in order to ride the roller coaster. Since he can’t wait, he puts on a pair of boots that add 1\(\frac{1}{6}\) inches to his height and slips an insole inside to add another \(\frac{1}{8}\) inch to his height. Will this make Jackson appear tall enough to ride the roller coaster?
Answer:
Fraction of Height required to ride a roller coaster for Jackson = 1\(\frac{3}{4}\) inches.
Fraction of his height = 1\(\frac{1}{6}\) inches = \(\frac{7}{6}\)
Fraction of his boots length = \(\frac{1}{8}\) inches
Total fraction of his height with boots = \(\frac{7}{6}\) + \(\frac{1}{8}\) = \(\frac{28}{24}\) + \(\frac{3}{24}\) = \(\frac{31}{24}\) = 1\(\frac{7}{24}\) .
1\(\frac{3}{4}\) = multiply by 6 both numerator and denominator = 1\(\frac{18}{24}\)
therefore, 1\(\frac{18}{24}\) > is greater than 1\(\frac{7}{24}\) So, he is not taller enough to ride roller coaster .
So, he cant ride the roller coaster .
Question 6.
A baker needs 5 lb of butter for a recipe. She found 2 portions that each weigh 1\(\frac{1}{6}\) lb and a portion that weighs 2\(\frac{2}{7}\) lb. Does she have enough butter for her recipe?
Answer:
Fraction of butter required for a recipe = 5 lb
Fraction of 2 portions that weigh = 2 × \(\frac{7}{6}\) lb = \(\frac{7}{3}\)
Fraction of portions that weighs = 2\(\frac{2}{7}\) lb. = \(\frac{16}{7}\) lb.
Fraction of butter of portions = \(\frac{7}{3}\) + \(\frac{16}{7}\) = \(\frac{49}{21}\) + \(\frac{48}{21}\) = \(\frac{97}{21}\) = 4\(\frac{13}{21}\)
Therefore, she doesnot have enough butter for the recipe = 4\(\frac{13}{21}\)
Eureka Math Grade 5 Module 3 Lesson 13 Exit Ticket Answer Key
Question 1.
Circle the correct answer.
a. \(\frac{1}{2}\) +\(\frac{5}{12}\) greater than 1 less than 1
b. 2\(\frac{7}{8}\) – 1\(\frac{7}{9}\) greater than 1 less than 1
c. 1\(\frac{1}{12}\) – \(\frac{7}{10}\) greater than \(\frac{1}{2}\) less than \(\frac{1}{2}\)
d. \(\frac{3}{7}\) + \(\frac{1}{8}\) greater than \(\frac{1}{2}\) less than \(\frac{1}{2}\)
Answer:
a. \(\frac{1}{2}\) +\(\frac{5}{12}\) = \(\frac{11}{12}\)
b.2\(\frac{7}{8}\) – 1\(\frac{7}{9}\) = 8\(\frac{7}{9}\)
c. 1\(\frac{1}{12}\) – \(\frac{7}{10}\) = \(\frac{23}{60}\)
d. \(\frac{3}{7}\) + \(\frac{1}{8}\) = \(\frac{31}{56}\)
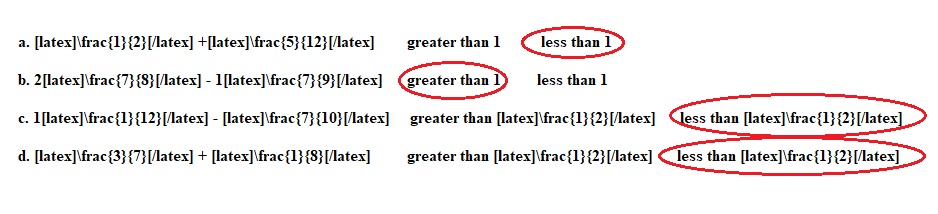
Explanation :
a. \(\frac{1}{2}\) +\(\frac{5}{12}\)
lcm of 2 and 12 is 12.
\(\frac{6}{12}\) +\(\frac{5}{12}\) = \(\frac{11}{12}\) less than 1
b. 2\(\frac{7}{8}\) – 1\(\frac{7}{9}\) = \(\frac{23}{8}\) – \(\frac{16}{9}\)
lcm of 8 and 9 is 72.
\(\frac{207}{72}\) – \(\frac{128}{9}\) = \(\frac{79}{9}\) = 8\(\frac{7}{9}\) greater than1.
c. . 1\(\frac{1}{12}\) – \(\frac{7}{10}\) = . \(\frac{13}{12}\) – \(\frac{7}{10}\)
lcm of 12 and 10 is 60.
. \(\frac{65}{60}\) – \(\frac{42}{60}\) = \(\frac{23}{60}\) less than 1 .
d. \(\frac{3}{7}\) + \(\frac{1}{8}\)
lcm of 7 and 8 is 56
\(\frac{24}{56}\) + \(\frac{7}{56}\) = \(\frac{31}{56}\) = less than 1 .
Question 2.
Use > , < , or = to make the following statement true.
4\(\frac{4}{5}\) + 3\(\frac{2}{3}\) < 8\(\frac{1}{2}\)
Answer:
4\(\frac{4}{5}\) + 3\(\frac{2}{3}\) < 8\(\frac{1}{2}\)
Explanation :
4\(\frac{4}{5}\) + 3\(\frac{2}{3}\) = \(\frac{24}{5}\) + \(\frac{11}{3}\)
lcm of 5 and 3 is 15 .
\(\frac{72}{15}\) + \(\frac{55}{15}\) = \(\frac{127}{15}\) = 8 \(\frac{7}{15}\)
Eureka Math Grade 5 Module 3 Lesson 13 Homework Answer Key
Question 1.
Are the following expressions greater than or less than 1? Circle the correct answer.
a. \(\frac{1}{2}\) + \(\frac{4}{9}\) greater than 1 less than 1
b. \(\frac{5}{8}\) + \(\frac{3}{5}\) greater than 1 less than 1
c. 1\(\frac{1}{5}\) – \(\frac{1}{3}\) greater than 1 less than 1
d. 4\(\frac{3}{5}\) – 3\(\frac{3}{4}\) greater than 1 less than 1
Answer:
a. \(\frac{1}{2}\) + \(\frac{4}{9}\) = \(\frac{17}{18}\) less than 1.
b. \(\frac{5}{8}\) + \(\frac{3}{5}\) = 1 \(\frac{9}{40}\) greater than 1 .
c. 1\(\frac{1}{5}\) – \(\frac{1}{3}\) = \(\frac{13}{15}\) less than 1.
d. 4\(\frac{3}{5}\) – 3\(\frac{3}{4}\) = \(\frac{17}{20}\) less than 1 .
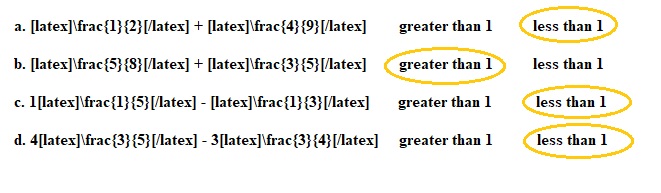
Explanation :
a. \(\frac{1}{2}\) + \(\frac{4}{9}\)
lcm of 2 and 9 is 18.
\(\frac{9}{18}\) + \(\frac{8}{18}\) = \(\frac{17}{18}\)
b. \(\frac{5}{8}\) + \(\frac{3}{5}\)
lcm of 8 and 5 is 40 .
\(\frac{25}{40}\) + \(\frac{24}{40}\) = \(\frac{49}{40}\) =1 \(\frac{9}{40}\)
c. 1\(\frac{1}{5}\) – \(\frac{1}{3}\) = \(\frac{6}{5}\) – \(\frac{1}{3}\)
lcm of 5 and 3 is 15 .
\(\frac{18}{15}\) – \(\frac{5}{15}\) = \(\frac{13}{15}\)
d. 4\(\frac{3}{5}\) – 3\(\frac{3}{4}\) = \(\frac{23}{5}\) – \(\frac{15}{4}\)
lcm of 5 and 4 is 20 .
\(\frac{92}{20}\) – \(\frac{75}{20}\) = \(\frac{17}{20}\)
Question 2.
Are the following expressions greater than or less than \(\frac{1}{2}\)? Circle the correct answer.
a. \(\frac{1}{5}\) + \(\frac{1}{4}\) greater than \(\frac{1}{2}\) less than \(\frac{1}{2}\)
b. \(\frac{6}{7}\) – \(\frac{1}{6}\) greater than \(\frac{1}{2}\) less than \(\frac{1}{2}\)
c. 1\(\frac{1}{7}\) – \(\frac{5}{6}\) greater than \(\frac{1}{2}\) less than \(\frac{1}{2}\)
d. \(\frac{4}{7}\) + \(\frac{1}{8}\) greater than \(\frac{1}{2}\) less than \(\frac{1}{2}\)
Answer:
a. \(\frac{1}{5}\) + \(\frac{1}{4}\) = \(\frac{9}{20}\) less than \(\frac{1}{2}\)
b. \(\frac{6}{7}\) – \(\frac{1}{6}\) = \(\frac{29}{42}\) greater than \(\frac{1}{2}\)
c. 1\(\frac{1}{7}\) – \(\frac{5}{6}\) = \(\frac{13}{42}\) less than \(\frac{1}{2}\)
d. \(\frac{4}{7}\) + \(\frac{1}{8}\) = \(\frac{39}{56}\) greater than \(\frac{1}{2}\)
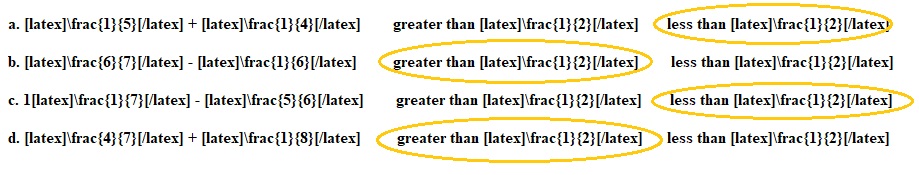
Explanation :
a. \(\frac{1}{5}\) + \(\frac{1}{4}\)
lcm of 5 and 4 is 20 .
\(\frac{4}{20}\) + \(\frac{5}{20}\) = \(\frac{9}{20}\)
b. \(\frac{6}{7}\) – \(\frac{1}{6}\)
lcm of 7 and 6 is 42 .
\(\frac{36}{42}\) – \(\frac{7}{42}\) = \(\frac{29}{42}\)
c. 1\(\frac{1}{7}\) – \(\frac{5}{6}\) = \(\frac{8}{7}\) – \(\frac{5}{6}\)
lcm of 7 and 6 is 42 .
\(\frac{48}{42}\) – \(\frac{35}{42}\) = \(\frac{13}{42}\)
d. \(\frac{4}{7}\) + \(\frac{1}{8}\)
lcm of 7 and 8 is 56 .
\(\frac{32}{56}\) + \(\frac{7}{56}\) = \(\frac{39}{56}\)
Question 3.
Use > , < , or = to make the following statements true.
a. 5\(\frac{4}{5}\) + 2\(\frac{2}{3}\) _______ 8\(\frac{3}{4}\)
b. 3\(\frac{4}{7}\) – 2\(\frac{3}{5}\) _______ 1\(\frac{4}{7}\) + \(\frac{3}{5}\)
c. 4\(\frac{1}{2}\) + 1\(\frac{4}{9}\) _______ 5 + \(\frac{13}{18}\)
d. 10\(\frac{3}{8}\) – 7\(\frac{3}{5}\) _______ 3\(\frac{3}{8}\) + \(\frac{3}{5}\)
Answer:
a. 5\(\frac{4}{5}\) + 2\(\frac{2}{3}\) < 8\(\frac{3}{4}\)
b. 3\(\frac{4}{7}\) – 2\(\frac{3}{5}\) < 1\(\frac{4}{7}\) + \(\frac{3}{5}\)
c. 4\(\frac{1}{2}\) + 1\(\frac{4}{9}\) < 5 + \(\frac{13}{18}\)
d. 10\(\frac{3}{8}\) – 7\(\frac{3}{5}\) > 3\(\frac{3}{8}\) + \(\frac{3}{5}\)
Explanation :
a. 5\(\frac{4}{5}\) + 2\(\frac{2}{3}\) = \(\frac{29}{5}\) + \(\frac{8}{3}\)
lcm of 5 and 3 is 15 .
\(\frac{57}{15}\) + \(\frac{40}{15}\) = \(\frac{97}{15}\) = 6\(\frac{7}{15}\) .
b. 3\(\frac{4}{7}\) – 2\(\frac{3}{5}\) = \(\frac{25}{7}\) – \(\frac{13}{5}\) .
lcm of 7 and 5 is 35 .
\(\frac{125}{35}\) – \(\frac{91}{35}\) = \(\frac{34}{35}\)
1\(\frac{4}{7}\) + \(\frac{3}{5}\) = \(\frac{11}{7}\) + \(\frac{3}{5}\)
lcm of 5 and 7 is 35 .
\(\frac{55}{35}\) + \(\frac{21}{35}\) = \(\frac{76}{35}\) = 2 \(\frac{6}{35}\)
c. 4\(\frac{1}{2}\) + 1\(\frac{4}{9}\) = \(\frac{9}{2}\) + \(\frac{13}{9}\)
lcm of 2 and 9 is 18 .
4\(\frac{1}{2}\) + 1\(\frac{4}{9}\)
5 + \(\frac{13}{18}\) = \(\frac{90}{18}\) + \(\frac{13}{18}\) = \(\frac{103}{18}\) = 5\(\frac{13}{18}\)
d. 10\(\frac{3}{8}\) – 7\(\frac{3}{5}\) = \(\frac{83}{8}\) – \(\frac{38}{5}\)
lcm of 8 and 5 is 40 .
\(\frac{415}{40}\) – \(\frac{304}{40}\) = \(\frac{311}{40}\) = 7\(\frac{31}{40}\)
3\(\frac{3}{8}\) + \(\frac{3}{5}\) = \(\frac{27}{8}\) + \(\frac{3}{5}\)
lcm of 8 and 5 is 40 .
\(\frac{135}{40}\) + \(\frac{24}{40}\) = \(\frac{159}{40}\)= 3\(\frac{39}{40}\)
Question 4.
Is it true that 5\(\frac{2}{3}\) – 3\(\frac{3}{4}\) = 1 + \(\frac{2}{3}\) + \(\frac{3}{4}\)? Prove your answer.
Answer:
It is not true .
5\(\frac{2}{3}\) – 3\(\frac{3}{4}\) < 1 + \(\frac{2}{3}\) + \(\frac{3}{4}\)
Explanation :
5\(\frac{2}{3}\) – 3\(\frac{3}{4}\) = \(\frac{17}{3}\) – \(\frac{15}{4}\)
lcm of 3 and 4 is 12.
\(\frac{68}{12}\) – \(\frac{45}{12}\) = \(\frac{23}{12}\) = 1\(\frac{11}{12}\)
1 + \(\frac{2}{3}\) + \(\frac{3}{4}\)
lcm of 3 and 4 is 12 .
\(\frac{12}{12}\) + \(\frac{8}{12}\) + \(\frac{9}{12}\) = \(\frac{29}{12}\) = 2\(\frac{5}{12}\) .
Question 5.
A tree limb hangs 5\(\frac{1}{4}\) feet from a telephone wire. The city trims back the branch before it grows within 2 \(\frac{1}{2}\) feet of the wire. Will the city allow the tree to grow 2\(\frac{3}{4}\) more feet?
Answer:
Fraction of height at which telephone wire is hung = 5\(\frac{1}{4}\) =\(\frac{21}{4}\) feet
Fraction of height city allow the tree to grow = 2\(\frac{3}{4}\) = \(\frac{11}{4}\) feet .
Fraction of height city trims back the branch before it grows = 2\(\frac{1}{2}\) = \(\frac{5}{2}\) feet
Fraction of height of telephone wire can be hang = \(\frac{21}{4}\) – \(\frac{11}{4}\) = \(\frac{10}{4}\) = \(\frac{5}{2}\)
both are equal that means the tree will be trim back .
Question 6.
Mr. Kreider wants to paint two doors and several shutters. It takes 2\(\frac{1}{8}\) gallons of paint to coat each door and 1\(\frac{3}{5}\) gallons of paint to coat all of his shutters. If Mr. Kreider buys three 2-gallon cans of paint, does he have enough to complete the job?
Answer:
Fraction of cost of paint to coat each door = 2\(\frac{1}{8}\) gallons = \(\frac{17}{8}\)
Fraction of cost of paint to coat all his shutters = 1\(\frac{3}{5}\) gallons = \(\frac{8}{5}\)
Fraction of cost to paint 2 doors and shutters = 2 × \(\frac{17}{8}\) + \(\frac{8}{5}\) = \(\frac{17}{4}\) + \(\frac{8}{5}\) = \(\frac{85}{20}\) + \(\frac{32}{20}\) = \(\frac{117}{20}\) = 5latex]\frac{17}{20}[/latex]
Total paint = three 2-gallon cans of paint = 3 × 2 = 6 gallons.
Therefore Kreider doesn’t have sufficient amount of paint .