Engage NY Eureka Math 4th Grade Module 5 Lesson 23 Answer Key
Eureka Math Grade 4 Module 5 Lesson 23 Problem Set Answer Key
Question 1.
Circle any fractions that are equivalent to a whole number. Record the whole number below the fraction.
a. Count by 1 thirds. Start at 0 thirds. End at 6 thirds.
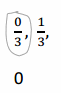
Answer:
0/3, 1/3, 2/3, 3/3, 4/3, 5/3, 6/3.
Explanation:
In the above-given question,
given that,
circle any fractions that are equivalent to a whole number.
count by 1 third.
start at 0 thirds.
end at 6 thirds.
0/3 + 1 = 1/3.
1/3 + 1 = 2/3.
2/3 + 1 = 3/3.
3/3 + 1 = 4/3.
4/3 + 1 = 5/3.
5/3 + 1 = 6/3.
0/3 = 0, 3/3 = 1, 6/3 = 2.
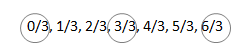
b. Count by 1 halves. Start at 0 halves. End at 8 halves.
Answer:
0/2, 1/2, 2/2, 3/2, 4/2, 5/2, 6/2, 7/2, 8/2.
Explanation:
In the above-given question,
given that,
circle any fractions that are equivalent to a whole number.
count by 1 half.
start at 0 halves.
end at 8 halves.
0/2 + 1 = 1/2.
1/2 + 1 = 2/2.
2/2 + 1 = 3/2.
3/2 + 1 = 4/2.
4/2 + 1 = 5/2.
5/2 + 1 = 6/2.
6/2 + 1 = 7/2.
7/2 + 1 = 8/2.
0/2 = 0, 2/2 = 1, 4/2 = 2, 6/2 = 3, 8/2 = 4.
![]()
Question 2.
Use parentheses to show how to make ones in the following number sentence.
\(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) = 3
Answer:
1/4 + 1/4 + 1/4 + 1/4 + 1/4 + 1/4 + 1/4 + 1/4 + 1/4 + 1/4 + 1/4 + 1/4.
Explanation:
In the above-given question,
given that,
use parantheses to make ones .
(1/4) + (1/4) + (1/4) + (1/4).
1/4 = 0.25.
0.25 + 0.25 + 0.25 + 0.25.
0.50 + 0.50 = 1.
1 + 1 + 1 = 3.
Question 3.
Multiply, as shown below. Draw a number line to support your answer.
a. 6 × \(\frac{1}{3}\)
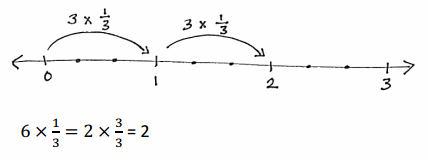
Answer:
6 x 1/3 = 2.
Explanation:
In the above-given question,
given that,
6 x 1/3.
3 x 1/3 + 3 x 1/3.
2 x 3/3 = 2.
2 x 1 = 2.
b. 6 × \(\frac{1}{2}\)
Answer:
6 x 1/2 = 3.
Explanation:
In the above-given question,
given that,
6 x 1/2.
3 x 1/2 + 3 x 1/2.
3 x 2/2 = 3.
3 x 1 = 3.
c. 12 × \(\frac{1}{4}\)
Answer:
12 x 1/4 = 3.
Explanation:
In the above-given question,
given that,
12 x 1/4.
6 x 1/4 + 6 x 1/4.
6 x 2/2 = 3.
3 x 1 = 3.
Question 4.
Multiply, as shown below. Write the product as a mixed number. Draw a number line to support your answer.
a. 7 copies of 1 third
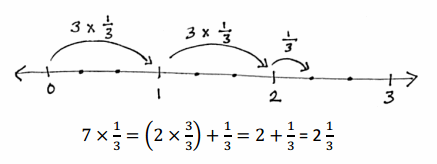
Answer:
7 x 1/3 = 7/3 = 2(1/3).
Explanation:
In the above-given question,
given that,
write the product as a mixed number.
7 x 1/3.
(2 x 3/3) + 1/3.
2 + 1/3.
2(1/3).
b. 7 copies of 1 half
Answer:
7 x 1/2 = 7/2 = 3(1/2).
Explanation:
In the above-given question,
given that,
write the product as a mixed number.
7 x 1/2.
(3 x 2/2) + 1/2.
3 + 1/2.
3(1/2).
c. 10 × \(\frac{1}{4}\)
Answer:
10 x 1/4 = 10/4 = 2(2/4).
Explanation:
In the above-given question,
given that,
write the product as a mixed number.
10 x 1/4.
(2 x 4/4) + 2/4.
2 + 2/4.
2(2/4).
d. 14 × \(\frac{1}{3}\)
Answer:
14 x 1/3 = 14/3 = 4(2/3).
Explanation:
In the above-given question,
given that,
write the product as a mixed number.
14 x 1/3.
(4 x 3/3) + 2/3.
4 + 2/3.
4(2/3).
Eureka Math Grade 4 Module 5 Lesson 23 Exit Ticket Answer Key
Multiply and write the product as a mixed number. Draw a number line to support your answer.
Question 1.
8 × \(\frac{1}{2}\)
Answer:
8 x 1/2 = 4.
Explanation:
In the above-given question,
given that,
8 x 1/2.
4 x 1/2 + 4 x 1/2.
4 x 2/2 = 4.
4 x 1 = 4.
Question 2.
7 copies of 1 fourth
Answer:
7 x 1/4 = 7/4 = 4(3/4).
Explanation:
In the above-given question,
given that,
write the product as a mixed number.
7 x 1/4.
(4 x 2/2) + 3/4.
4 + 3/4.
4(3/4).
Question 3.
13 × \(\frac{1}{3}\)
Answer:
13 x 1/3 = 13/3.
Explanation:
In the above-given question,
given that,
13 x 1/3.
6 x 1/3 + 7 x 1/3.
13 x 1/3.
13/3.
Eureka Math Grade 4 Module 5 Lesson 23 Homework Answer Key
Question 1.
Circle any fractions that are equivalent to a whole number. Record the whole number below the fraction.
a. Count by 1 fourths. Start at 0 fourths. Stop at 6 fourths.
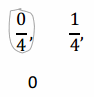
Answer:
0/4, 1/4, 2/4, 3/4, 4/4, 5/4, 6/4.
Explanation:
In the above-given question,
given that,
circle any fractions that are equivalent to a whole number.
count by 1 fourth.
start at 0 fourths.
end at 6 fourths.
0/4 + 1 = 1/4.
1/4 + 1 = 2/4.
2/4 + 1 = 3/4.
3/4 + 1 = 4/4.
4/4 + 1 = 5/4.
5/4 + 1 = 6/4.
0/4 = 0, 2/4 = 2, 4/4 = 1.
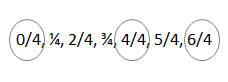
b. Count by 1 sixths. Start at 0 sixths. Stop at 14 sixths.
Answer:
0/6, 1/6, 2/6, 3/6, 4/6, 5/6, 6/6, 7/6, 8/6, 9/6, 10/6, 11/6, 12/6, 13/6, 14/6.
Explanation:
In the above-given question,
given that,
circle any fractions that are equivalent to a whole number.
count by 1 sixth.
start at 0 sixths.
end at 14 sixths.
0/6 + 1 = 1/6.
1/6 + 1 = 2/6.
2/6 + 1 = 3/6.
3/6 + 1 = 4/6.
4/6 + 1 = 5/6.
5/6 + 1 = 6/6.
6/6 + 1 = 7/6.
7/6 + 1 = 8/6.
8/6 + 1 = 9/6.
9/6 + 1 = 10/6.
10/6 + 1 = 11/6.
11/6 + 1 = 12/6.
12/6 + 1 = 13/6.
13/6 + 1 = 14/6.
0/6 = 0, 12/6 = 2, 6/6 = 1.
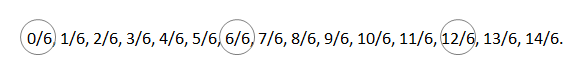
Question 2.
Use parentheses to show how to make ones in the following number sentence.
\(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\) = 4
Answer:
1/3 + 1/3 + 1/3 + 1/3 + 1/3 + 1/3 + 1/3 + 1/3 + 1/3 + 1/3 + 1/3 + 1/3.
Explanation:
In the above-given question,
given that,
use parantheses to make ones .
(1/3) + (1/3) + (1/3) + (1/3).
1/3 = 0.75.
0.75 + 0.75 + 0.75 + 0.75.
1.5 + 1.5 = 3.
3 + 1 = 4.
Question 3.
Multiply, as shown below. Draw a number line to support your answer.
a. 6 × \(\frac{1}{3}\)
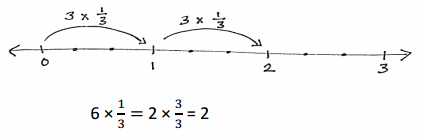
Answer:
6 x 1/3 = 2.
Explanation:
In the above-given question,
given that,
6 x 1/3.
3 x 1/3 + 3 x 1/3.
2 x 3/3 = 2.
2 x 1 = 2.
b. 10 × \(\frac{1}{2}\)
Answer:
10 x 1/2 = 5.
Explanation:
In the above-given question,
given that,
10 x 1/2.
5 x 1/2 + 5 x 1/2.
5 x 2/2 = 5.
5 x 1 = 5.
c. 8 × \(\frac{1}{4}\)
Answer:
8 x 1/4 = 2.
Explanation:
In the above-given question,
given that,
8 x 1/4.
4 x 1/4 + 4 x 1/4.
2 x 4/4 = 2.
2 x 1 = 2.
Question 4.
Multiply, as shown below. Write the product as a mixed number. Draw a number line to support your answer.
a. 7 copies of 1 third
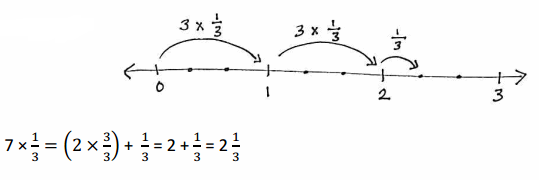
Answer:
7 x 1/3 = 7/3 = 2(1/3).
Explanation:
In the above-given question,
given that,
write the product as a mixed number.
7 x 1/3.
(2 x 3/3) + 1/3.
2 + 1/3.
2(1/3).
b. 7 copies of 1 fourth
Answer:
7 x 1/4 = 7/4 = 1(3/4).
Explanation:
In the above-given question,
given that,
write the product as a mixed number.
7 x 1/4.
(1 x 4/4) + 3/4.
1 + 3/4.
1(3/4).
c. 11 groups of 1 fifth
Answer:
11 x 1/5 = 11/5 = 2(1/5).
Explanation:
In the above-given question,
given that,
write the product as a mixed number.
11 x 1/5.
( 2 x 5/5) + 1/5.
2 + 1/5.
2(1/5).
d. 7 × \(\frac{1}{2}\)
Answer:
7 x 1/2 = 7/2 = 3(1/2).
Explanation:
In the above-given question,
given that,
write the product as a mixed number.
7 x 1/2.
(3 x 2/2) + 1/2.
3 + 1/2.
3(1/2).
e. 9 × \(\frac{1}{5}\)
Answer:
9 x 1/5 = 9/5 = 1(4/5).
Explanation:
In the above-given question,
given that,
write the product as a mixed number.
9 x 1/5.
(1 x 5/5) + 4/5.
1 + 4/5.
1(4/5).