Engage NY Eureka Math 4th Grade Module 5 Lesson 18 Answer Key
Eureka Math Grade 4 Module 5 Lesson 18 Practice Sheet Answer Key
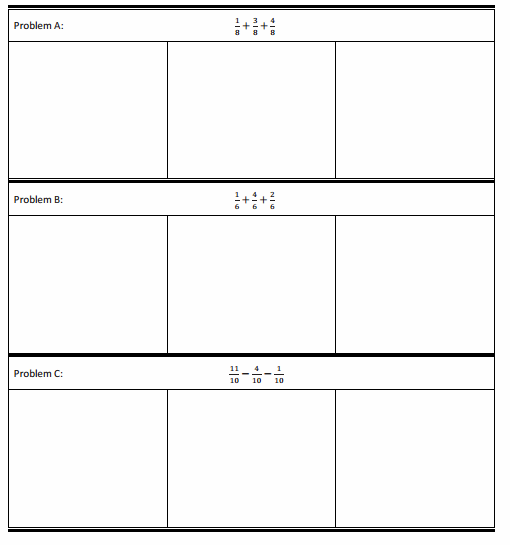
Answer:
1/8 + 3/8 + 4/8= 1.
Explanation:
In the above-given question,
given that,
1/8 + 3/8.
4/8.
4/8 + 4/8.
8/8 = 1.
Answer:
1/6 + 4/6 + 2/6= 7/6.
Explanation:
In the above-given question,
given that,
1/6 + 4/6.
5/6.
5/6 + 2/6.
7/6.
Answer:
11/10 – 4/10 – 1/10 = 6/10.
Explanation:
In the above-given question,
given that,
11/10 – 4/10.
7/10 – 1/10.
6/10._____________
adding and subt

Answer:
1 – 3/12 – 5/12 = 4/12.
Explanation:
In the above-given question,
given that,
1 – 3/12.
9/12.
9/12 – 5/12.
4/12.
Answer:
5/8 + 4/8 + 1/8= 10/8.
Explanation:
In the above-given question,
given that,
5/8 + 4/8.
9/8.
9/8 + 1/8.
10/8.
Answer:
1(1/5) – 2/5 – 3/5= 1/5.
Explanation:
In the above-given question,
given that,
1(1/5) – 2/5.
6/5 – 2/5.
4/5 – 1/5.
3/5.
Eureka Math Grade 4 Module 5 Lesson 18 Problem Set Answer Key
Question 1.
Show one way to solve each problem. Express sums and differences as a mixed number when possible. Use number bonds when it helps you. Part (a) is partially completed.
a. \(\frac{2}{5}\) + \(\frac{3}{5}\) + \(\frac{1}{5}\)
= \(\frac{5}{5}\) + \(\frac{1}{5}\) = 1 + \(\frac{1}{5}\)
=1 \(\frac{1}{5}\).
Answer:
1\(\frac{1}{5}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{2}{5}\) + \(\frac{3}{5}\) + \(\frac{1}{5}\)
2/5 + 3/5 = 5/5.
\(\frac{5}{5}\) + \(\frac{1}{5}\).
5/5 = 1.
5/5 + 1/5 = 6/5.
1\(\frac{1}{5}\).
b. \(\frac{3}{6}\) + \(\frac{1}{6}\) + \(\frac{3}{6}\)
Answer:
1\(\frac{1}{6}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{3}{6}\) + \(\frac{1}{6}\) + \(\frac{3}{6}\)
3/6 + 1/6 = 4/6.
\(\frac{4}{6}\) + \(\frac{3}{6}\).
4/6 + 3/6.
7/6.
1\(\frac{1}{6}\).
c. \(\frac{5}{7}\) + \(\frac{7}{7}\) + \(\frac{2}{7}\)
Answer:
\(\frac{14}{7}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{5}{7}\) + \(\frac{7}{7}\) + \(\frac{2}{7}\)
5/7 + 7/7 = 12/7.
\(\frac{12}{7}\) + \(\frac{2}{7}\).
12/7 + 2/7 = 14/7.
1\(\frac{7}{7}\).
d. \(\frac{7}{8}\) – \(\frac{3}{8}\) – \(\frac{1}{8}\)
Answer:
\(\frac{3}{8}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{7}{8}\) – \(\frac{3}{8}\) – \(\frac{1}{8}\)
7/8 – 3/8 = 4/8.
\(\frac{4}{8}\) – \(\frac{1}{8}\).
4/8 – 1/8 = 3/8.
1\(\frac{5}{8}\).
e. \(\frac{7}{9}\) + \(\frac{1}{9}\) + \(\frac{4}{9}\)
Answer:
\(\frac{12}{9}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{7}{9}\) + \(\frac{1}{9}\) + \(\frac{4}{9}\)
7/9 + 1/9 = 8/9.
\(\frac{8}{9}\) + \(\frac{4}{9}\).
8/9 + 4/9 = 12/9.
1\(\frac{3}{9}\).
f. \(\frac{4}{10}\) + \(\frac{11}{10}\) + \(\frac{5}{10}\)
Answer:
\(\frac{20}{10}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{4}{10}\) + \(\frac{11}{10}\) + \(\frac{5}{10}\)
4/10 + 11/10 = 15/10.
\(\frac{15}{10}\) + \(\frac{5}{10}\).
15/10 + 5/10 = 20/10.
1\(\frac{10}{10}\).
g. 1 – \(\frac{3}{12}\) – \(\frac{4}{12}\)
Answer:
\(\frac{5}{12}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{12}{12}\) – \(\frac{3}{12}\) – \(\frac{4}{12}\)
12 – 3/12 = 9/12.
\(\frac{9}{12}\) – \(\frac{4}{12}\).
9/12 – 4/12 = 5/12.
1 – \(\frac{7}{12}\).
h. 1\(\frac{2}{3}\) – \(\frac{1}{3}\) – \(\frac{1}{3}\)
Answer:
\(\frac{0}{3}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{2}{3}\) – \(\frac{1}{3}\) – \(\frac{1}{3}\)
2/3 – 1/3 = 1/3.
\(\frac{1}{3}\) – \(\frac{1}{3}\).
1/3 – 1/3 = 0.
\(\frac{0}{3}\).
i. \(\frac{10}{12}\) + \(\frac{5}{12}\) + \(\frac{2}{12}\) + \(\frac{7}{12}\)
Answer:
\(\frac{24}{12}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{10}{12}\) + \(\frac{5}{12}\) + \(\frac{2}{12}\) + \(\frac{7}{12}\)
10/12 + 5/12 = 15/12.
\(\frac{15}{12}\) + \(\frac{2}{12}\).
15/12 + 2 /12 = 17/12.
\(\frac{17}{12}\) + \(\frac{7}{12}\).
17/12 + 7/12.
24/12.
1\(\frac{12}{12}\).
Question 2.
Monica and Stuart used different strategies to solve \(\frac{5}{8}\) + \(\frac{2}{8}\) + \(\frac{5}{8}\).

Whose strategy do you like best? Why?
Answer:
Stuart’s way is the best.
Explanation:
In the above-given question,
given that,
Monica and Stuart used different strategies to solve \(\frac{5}{8}\) + \(\frac{2}{8}\) + \(\frac{5}{8}\).
Monica explained in detail.
Stuart’s also explained in detail.
he explained in a simple way.
so Stuart’s way is the best.
Question 3.
You gave one solution for each part of Problem 1. Now, for each problem indicated below, give a different solution method.
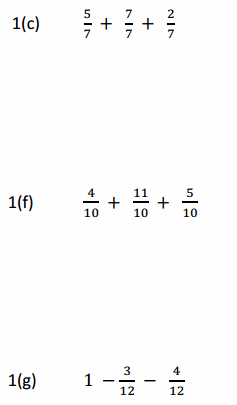
Answer:
e. 5/7 + 7/7 + 2/7 = 14/7.
Explanation:
In the above-given question,
given that,
5/7 + 7/7.
12/7.
12/7 + 2/7.
14/7.
5/7 + 7/7 + 2/7 = 14/7.
Answer:
f. 4/10 + 11/10 + 5/10 = 20/10.
Explanation:
In the above-given question,
given that,
4/10 + 11/10.
15/10.
15/10 + 5/10.
20/10.
4/10 + 11/10 + 5/10 = 20/10.
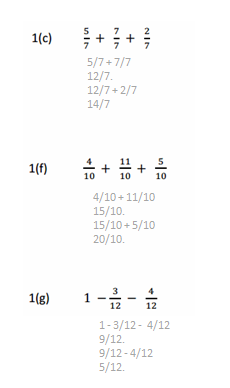
Eureka Math Grade 4 Module 5 Lesson 18 Exit Ticket Answer Key
Solve the following problems. Use number bonds to help you.
Question 1.
\(\frac{5}{9}\) + \(\frac{2}{9}\) + \(\frac{4}{9}\)
Answer:
\(\frac{11}{9}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{5}{9}\) + \(\frac{2}{9}\) + \(\frac{4}{9}\)
5/9 + 2/9 = 7/9.
\(\frac{7}{9}\) + \(\frac{4}{9}\).
7/9 + 4/9 = 11/9.
\(\frac{11}{9}\).
Question 2.
1 – \(\frac{5}{8}\) – \(\frac{1}{8}\)
Answer:
\(\frac{2}{8}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{8}{1}\) – \(\frac{5}{8}\) – \(\frac{1}{8}\)
8 – 5/8 = 3/8.
\(\frac{3}{8}\) – \(\frac{1}{8}\).
3/8 – 1/8 = 2/8.
\(\frac{2}{8}\).
Eureka Math Grade 4 Module 5 Lesson 18 Homework Answer Key
Question 1.
Show one way to solve each problem. Express sums and differences as a mixed number when possible. Use number bonds when it helps you. Part (a) is partially completed.
a. \(\frac{1}{3}\) + \(\frac{2}{3}\) + \(\frac{1}{3}\)
= \(\frac{3}{3}\) + \(\frac{1}{3}\) = 1 + \(\frac{1}{3}\)
= __4/3______
Answer:
1\(\frac{1}{3}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{3}{3}\) + \(\frac{1}{3}\) + \(\frac{1}{3}\)
1 + 1/3 =2 /3.
\(\frac{3}{3}\) + \(\frac{1}{3}\).
2/3 + 2/3 = 4/3.
1\(\frac{1}{3}\).
b. \(\frac{5}{8}\) + \(\frac{5}{8}\) + \(\frac{3}{8}\)
Answer:
1\(\frac{5}{8}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{5}{8}\) + \(\frac{5}{8}\) + \(\frac{3}{8}\)
5/8 + 5/8 = 10/8.
\(\frac{10}{8}\) + \(\frac{3}{8}\).
10/8 + 3/8 = 13/8.
1\(\frac{5}{8}\).
c. \(\frac{4}{6}\) + \(\frac{6}{6}\) + \(\frac{1}{6}\)
Answer:
1\(\frac{5}{6}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{4}{6}\) + \(\frac{6}{6}\) + \(\frac{1}{6}\)
4/6 + 6/6 = 10/6.
\(\frac{10}{6}\) + \(\frac{1}{6}\).
10/6 + 1/6 = 11/6.
1\(\frac{5}{6}\).
d. 1\(\frac{2}{12}\) – \(\frac{2}{12}\) – \(\frac{1}{12}\)
Answer:
1 – \(\frac{1}{12}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
1\(\frac{2}{12}\) – \(\frac{2}{12}\) – \(\frac{1}{12}\)
14/12 – 2/12 = 12/12.
\(\frac{12}{12}\) – \(\frac{1}{12}\).
1 – 1/12 = 11/12.
1 – \(\frac{11}{12}\).
e. \(\frac{5}{7}\) + \(\frac{1}{7}\) + \(\frac{4}{7}\)
Answer:
1\(\frac{3}{7}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{5}{7}\) + \(\frac{1}{7}\) + \(\frac{4}{7}\)
5/7 + 1/7 = 6/7.
\(\frac{6}{7}\) + \(\frac{4}{7}\).
6/7 + 4/7 = 10/7.
1\(\frac{3}{7}\).
f. \(\frac{4}{10}\) + \(\frac{7}{10}\) + \(\frac{9}{10}\)
Answer:
1\(\frac{10}{20}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{4}{10}\) + \(\frac{7}{10}\) + \(\frac{9}{10}\)
4/10 + 7/10 = 11/10.
\(\frac{11}{10}\) + \(\frac{9}{10}\).
11/10 + 9/10 = 20/10.
1\(\frac{10}{20}\).
g. 1 – \(\frac{3}{10}\) – \(\frac{1}{10}\)
Answer:
1 – \(\frac{4}{10}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
1 – \(\frac{3}{10}\) – \(\frac{1}{10}\).
10 – 3/10 = 7/10.
\(\frac{7}{10}\) – \(\frac{1}{10}\).
7/10 – 1/10 = 6/10.
1 – \(\frac{4}{10}\).
h. 1\(\frac{3}{5}\) – \(\frac{4}{5}\) – \(\frac{1}{5}\)
Answer:
1 – \(\frac{2}{5}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
1\(\frac{3}{5}\) – \(\frac{4}{5}\) – \(\frac{1}{5}\)
8/5 – 4/5 = 4/5.
\(\frac{4}{5}\) – \(\frac{1}{5}\).
4/5 – 1/5 = 3/5.
1\(\frac{2}{5}\).
i. \(\frac{10}{15}\) + \(\frac{7}{15}\) + \(\frac{12}{15}\) + \(\frac{1}{15}\)
Answer:
1\(\frac{15}{15}\).
Explanation:
In the above-given question,
given that,
Express sums and differences as a mixed number when possible.
\(\frac{10}{15}\) + \(\frac{7}{15}\) + \(\frac{12}{15}\) + \(\frac{1}{15}\).
10/15 + 7/15 = 17/15.
\(\frac{12}{15}\) + \(\frac{1}{15}\).
12/15 + 1/15 = 13/15.
13/15 + 17/15.
1\(\frac{15}{15}\).
Question 2.
Bonnie used two different strategies to solve \(\frac{5}{10}\) + \(\frac{4}{10}\) + \(\frac{3}{10}\).
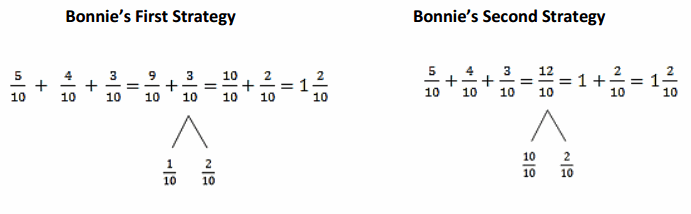
Which strategy do you like best? Why?
Answer:
Bonnie’s Second Strategy is the best.
Explanation:
In the above-given question,
given that,
Bonnie’s first and second used different strategies to solve \(\frac{5}{10}\) + \(\frac{4}{10}\) + \(\frac{3}{10}\).
Bonnie’s second strategy explained in detail.
Bonnie’s first strategy also explained in detail.
he explained in a simple way.
so the second way is the best.
Question 3.
You gave one solution for each part of Problem 1. Now, for each problem indicated below, give a different solution method.
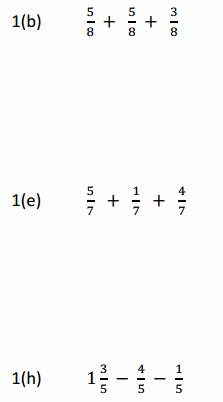
Answer:
b. 5/8 + 5/8 + 3/8 = 13/8.
Explanation:
In the above-given question,
given that,
5/8 + 5/8.
10/8.
10/8 + 3/8.
13/8.
5/8 + 5/8 + 3/8 = 13/8.
Answer:
e. 5/7 + 1/7 + 4/7 = 10/7.
Explanation:
In the above-given question,
given that,
5/7 + 1/7.
6/7.
6/7 + 4/7.
10/7.
5/7 + 1/7 + 4/7 = 10/7.
Answer:
h. 1(3/5) – 4/5 – 1/5 = 3/5.
Explanation:
In the above-given question,
given that,
1(3/5) – 4/5.
8/5 – 4/5.
4/5 – 3/5.
1/5.
1(3/5) – 4/5 – 1/5 = 3/5.
