Engage NY Eureka Math 3rd Grade Module 7 Lesson 21 Answer Key
Eureka Math Grade 3 Module 7 Lesson 21 Sprint Answer Key
A
Multiply or Divide by 3
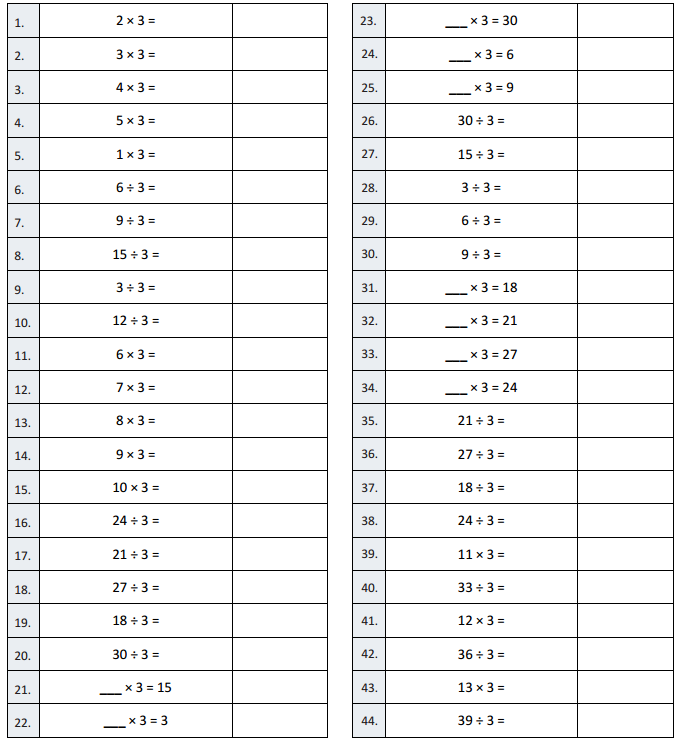
Answer:
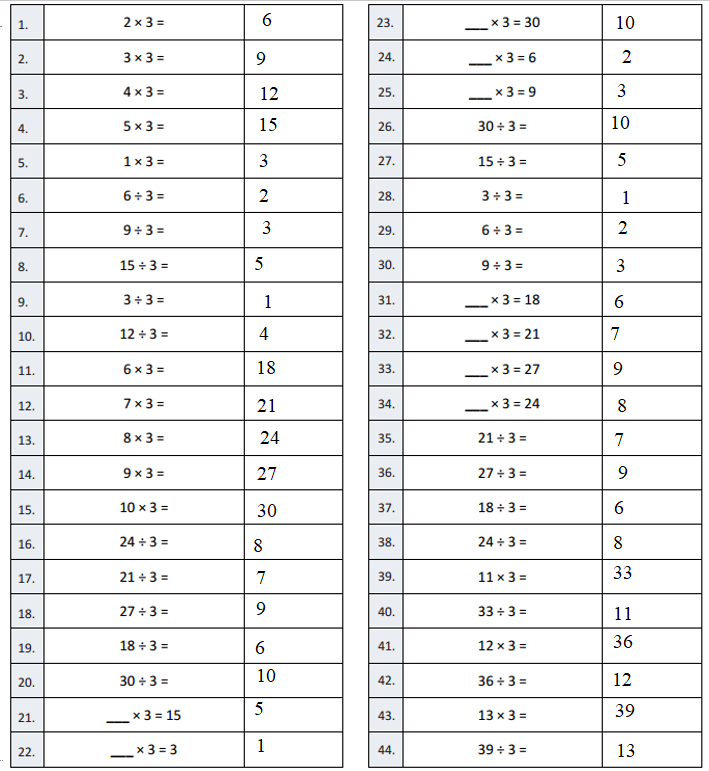
Question 1.
2 × 3 =
Answer:
2 × 3 = 6.
Question 2.
3 × 3 =
Answer:
3 × 3 = 9.
Question 3.
4 × 3 =
Answer:
4 × 3 = 12.
Question 4.
5 × 3 =
Answer:
5 × 3 = 15.
Question 5.
1 × 3 =
Answer:
1 × 3 = 3.
Question 6.
6 ÷ 3 =
Answer:
6 ÷ 3 = 2.
Question 7.
9 ÷ 3 =
Answer:
9 ÷ 3 = 3.
Question 8.
15 ÷ 3 =
Answer:
15 ÷ 3 = 5.
Question 9.
3 ÷ 3 =
Answer:
3 ÷ 3 = 1.
Question 10.
12 ÷ 3 =
Answer:
12 ÷ 3 = 4.
Question 11.
6 × 3 =
Answer:
6 × 3 = 18.
Question 12.
7 × 3 =
Answer:
7 × 3 = 21.
Question 13.
8 × 3 =
Answer:
8 × 3 = 24.
Question 14.
9 × 3 =
Answer:
9 × 3 = 27.
Question 15.
10 × 3 =
Answer:
10 × 3 = 30.
Question 16.
24 ÷ 3 =
Answer:
24 ÷ 3 = 8.
Question 17.
21 ÷ 3 =
Answer:
21 ÷ 3 = 7.
Question 18.
27 ÷ 3 =
Answer:
27 ÷ 3 = 9.
Question 19.
18 ÷ 3 =
Answer:
18 ÷ 3 = 6.
Question 20.
30 ÷ 3 =
Answer:
30 ÷ 3 = 10.
Question 21.
___ × 3 = 15
Answer:
5 × 3 = 15.
Question 22.
___ × 3 = 3
Answer:
1 × 3 = 3.
Question 23.
___ × 3 = 30
Answer:
10 × 3 = 30.
Question 24.
___ × 3 = 6
Answer:
2 × 3 = 6.
Question 25.
___ × 3 = 9
Answer:
3 × 3 = 9.
Question 26.
30 ÷ 3 =
Answer:
30 ÷ 3 = 10.
Question 27.
15 ÷ 3 =
Answer:
15 ÷ 3 = 5.
Question 28.
3 ÷ 3 =
Answer:
3 ÷ 3 = 1.
Question 29.
6 ÷ 3 =
Answer:
6 ÷ 3 = 2.
Question 30.
9 ÷ 3 =
Answer:
9 ÷ 3 = 3.
Question 31.
___ × 3 = 18
Answer:
6 × 3 = 18.
Question 32.
___ × 3 = 21
Answer:
7 × 3 = 21.
Question 33.
___ × 3 = 27
Answer:
9 × 3 = 27.
Question 34.
___ × 3 = 24
Answer:
8 × 3 = 24.
Question 35.
21 ÷ 3 =
Answer:
21 ÷ 3 = 7.
Question 36.
27 ÷ 3 =
Answer:
27 ÷ 3 = 9.
Question 37.
18 ÷ 3 =
Answer:
18 ÷ 3 = 6.
Question 38.
24 ÷ 3 =
Answer:
24 ÷ 3 = 8.
Question 39.
11 × 3 =
Answer:
11 × 3 = 33.
Question 40.
33 ÷ 3 =
Answer:
33 ÷ 3 = 11.
Question 41.
12 × 3 =
Answer:
12 × 3 = 36.
Question 42.
36 ÷ 3 =
Answer:
36 ÷ 3 = 12.
Question 43.
13 × 3 =
Answer:
13 × 3 = 39.
Question 44.
39 ÷ 3 =
Answer:
39 ÷ 3 = 13.
B
Multiply or Divide by 3
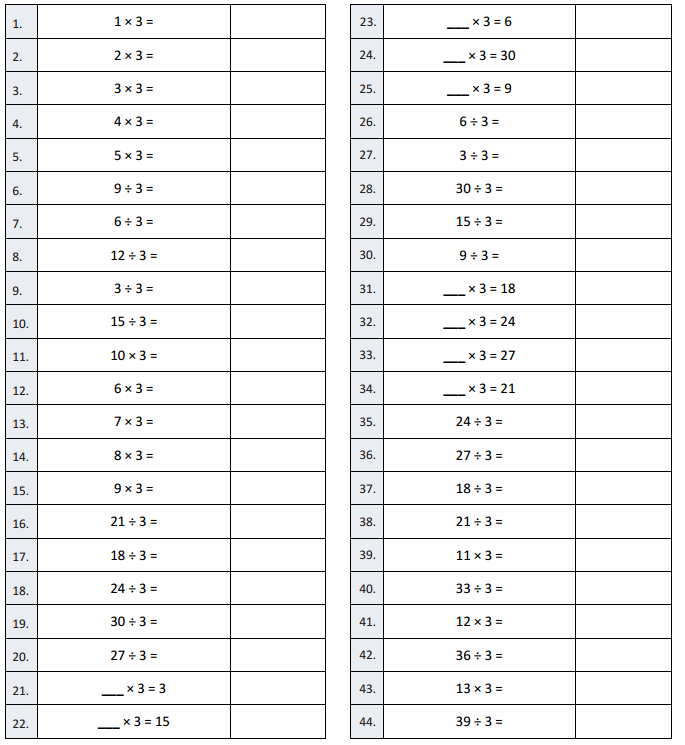
Answer:
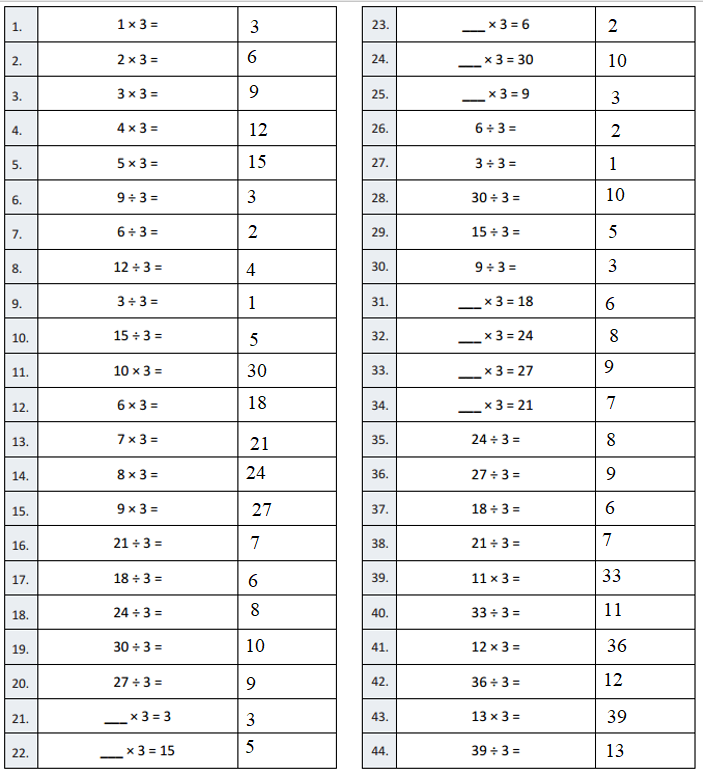
Question 1.
1 × 3 =
Answer:
1 × 3 = 3.
Question 2.
2 × 3 =
Answer:
2 × 3 = 6.
Question 3.
3 × 3 =
Answer:
3 × 3 = 9.
Question 4.
4 × 3 =
Answer:
4 × 3 = 12.
Question 5.
5 × 3 =
Answer:
5 × 3 = 15.
Question 6.
9 ÷ 3 =
Answer:
9 ÷ 3 = 3.
Question 7.
6 ÷ 3 =
Answer:
6 ÷ 3 = 2.
Question 8.
12 ÷ 3 =
Answer:
12 ÷ 3 = 4.
Question 9.
3 ÷ 3 =
Answer:
3 ÷ 3 = 1.
Question 10.
15 ÷ 3 =
Answer:
15 ÷ 3 = 5.
Question 11.
10 × 3 =
Answer:
10 × 3 = 30.
Question 12.
6 × 3 =
Answer:
6 × 3 = 18.
Question 13.
7 × 3 =
Answer:
7 × 3 = 21.
Question 14.
8 × 3 =
Answer:
8 × 3 = 24.
Question 15.
9 × 3 =
Answer:
9 × 3 = 27.
Question 16.
21 ÷ 3 =
Answer:
21 ÷ 3 = 7.
Question 17.
18 ÷ 3 =
Answer:
18 ÷ 3 = 6.
Question 18.
24 ÷ 3 =
Answer:
24 ÷ 3 = 8.
Question 19.
30 ÷ 3 =
Answer:
30 ÷ 3 = 10.
Question 20.
27 ÷ 3 =
Answer:
27 ÷ 3 = 9.
Question 21.
___ × 3 = 3
Answer:
1 × 3 = 3.
Question 22.
___ × 3 = 15
Answer:
5 × 3 = 15.
Question 23.
___ × 3 = 6
Answer:
2 × 3 = 6.
Question 24.
___ × 3 = 30
Answer:
10 × 3 = 30.
Question 25.
___ × 3 = 9
Answer:
3 × 3 = 9.
Question 26.
6 ÷ 3 =
Answer:
6 ÷ 3 = 2.
Question 27.
3 ÷ 3 =
Answer:
3 ÷ 3 = 1.
Question 28.
30 ÷ 3 =
Answer:
30 ÷ 3 = 10.
Question 29.
15 ÷ 3 =
Answer:
15 ÷ 3 = 5.
Question 30.
9 ÷ 3 =
Answer:
9 ÷ 3 = 3.
Question 31.
___ × 3 = 18
Answer:
6 × 3 = 18.
Question 32.
___ × 3 = 24
Answer:
8 × 3 = 24.
Question 33.
___ × 3 = 27
Answer:
9 × 3 = 27.
Question 34.
___ × 3 = 21
Answer:
7 × 3 = 21.
Question 35.
24 ÷ 3 =
Answer:
24 ÷ 3 = 8.
Question 36.
27 ÷ 3 =
Answer:
27 ÷ 3 = 9.
Question 37.
18 ÷ 3 =
Answer:
18 ÷ 3 = 6.
Question 38.
21 ÷ 3 =
Answer:
21 ÷ 3 = 7.
Question 39.
11 × 3 =
Answer:
11 × 3 = 33.
Question 40.
33 ÷ 3 =
Answer:
33 ÷ 3 = 11.
Question 41.
12 × 3 =
Answer:
12 × 3 = 36.
Question 42.
36 ÷ 3 =
Answer:
36 ÷ 3 = 12.
Question 43.
13 × 3 =
Answer:
13 × 3 = 39.
Question 44.
39 ÷ 3 =
Answer:
39 ÷ 3 = 13.
Eureka Math Grade 3 Module 7 Lesson 21 Problem Set Answer Key
Question 1.
On your centimeter grid paper, shade and label as many rectangles as you can with a perimeter of 16 centimeters.
a. Sketch the rectangles below, and label the side lengths.
b. Find the area of each rectangle you drew above.
Answer:
a. 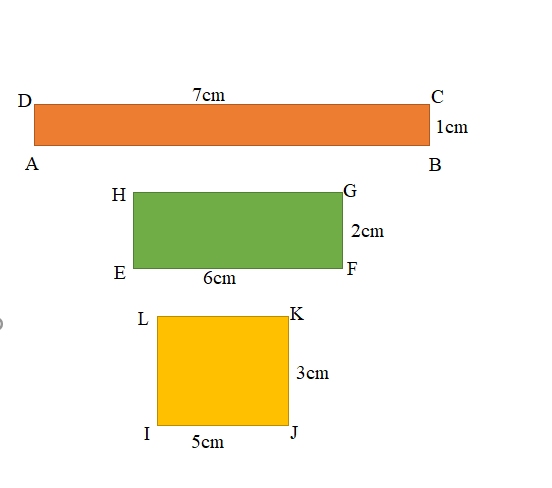
b. Area of the ABCD Rectangle = 7 square cm.
Area of the EFGH Rectangle = 12 square cm.
Area of the IJKL Rectangle = 15 square cm.
Explanation:
a. 
b.
Figure 1 : ABCD Rectangle
Length of the ABCD Rectangle = 7cm
Width of the ABCD Rectangle = 1cm
Area of the ABCD Rectangle = Length × Width
= 7cm × 1cm
= 7 square cm.
Figure 2 : EFGH Rectangle
Length of the EFGH Rectangle = 6cm
Width of the EFGH Rectangle = 2cm
Area of the EFGH Rectangle = Length × Width
= 6cm × 2cm
= 12 square cm.
Figure 3 : IJKL Rectangle
Length of the IJKL Rectangle = 5cm
Width of the IJKL Rectangle = 3cm
Area of the IJKL Rectangle = Length × Width
= 5cm × 3cm
= 15 square cm.
Question 2.
On your centimeter grid paper, shade and label as many rectangles as you can with a perimeter of 18 centimeters.
a. Sketch the rectangles below, and label the side lengths.
b. Find the area of each rectangle you drew above.
Answer:
a. 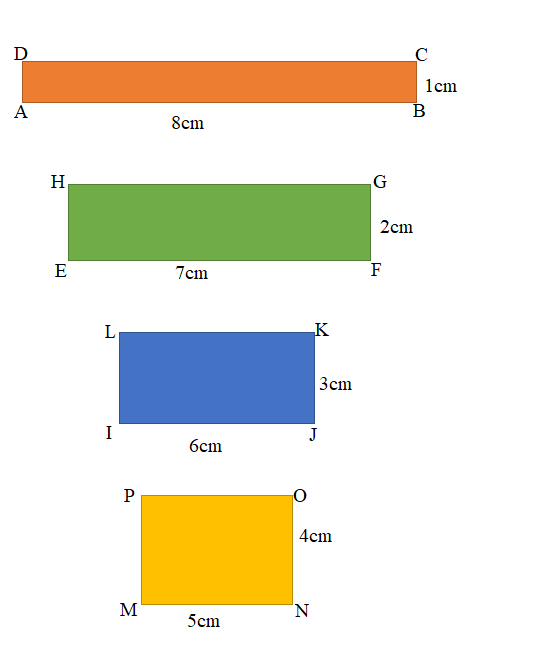
b. Area of the ABCD Rectangle = 8 square cm.
Area of the EFGH Rectangle = 14 square cm.
Area of the IJKL Rectangle = 18 square cm.
Area of the MNOP Rectangle = 20 square cm.
Explanation:
a.

b.
Figure 1 : ABCD Rectangle
Length of the ABCD Rectangle = 8cm
Width of the ABCD Rectangle = 1cm
Area of the ABCD Rectangle = Length × Width
= 8cm × 1cm
= 8 square cm.
Figure 2 : EFGH Rectangle
Length of the EFGH Rectangle = 7cm
Width of the EFGH Rectangle = 2cm
Area of the EFGH Rectangle = Length × Width
= 7cm × 2cm
= 14 square cm.
Figure 3 : IJKL Rectangle
Length of the IJKL Rectangle = 6cm
Width of the IJKL Rectangle = 3cm
Area of the IJKL Rectangle = Length × Width
= 6cm × 3cm
= 18 square cm.
Figure 4 : MNOP Rectangle
Length of the MNOP Rectangle = 5cm
Width of the MNOP Rectangle = 4cm
Area of the MNOP Rectangle = Length × Width
= 5cm × 4cm
= 20 square cm.
Question 3.
Use centimeter grid paper to shade in as many rectangles as you can with the given perimeters.
a. Use the charts below to show how many rectangles you shaded for each given perimeter. You might not use all the spaces in the charts.
| Perimeter = 10 cm Number of rectangles I made: _____ |
||
| Width | Length | Area |
| 1 cm | 4 cm | 4 square cm |
| Perimeter = 20 cm Number of rectangles I made: _____ |
||
| Width | Length | Area |
| 1 cm | 9 cm | 9 square cm |
| 3 cm | 7 cm | 21 square cm |
| 4 cm | 6 cm | 24 square cm |
| 5 cm | 5 cm | 25 square cm |
b. Did you make a square with either of the given perimeters? How do you know?
Answer:
Yes, I have made a square with lengths of the given perimeters of 20cm. I know it because a rectangle with the side length all equal to 5cm and a rectangle with all equal sides is to be known as Square.
Explanation:
Yes, because a rectangle with side length all equal to 5cm and a rectangle with all equal sides is to be known as Square.
Question 4.
Macy and Gavin both draw rectangles with perimeters of 16 centimeters. Use words and pictures to explain how it is possible for Macy’s and Gavin’s rectangles to have the same perimeters but different areas.
Answer:
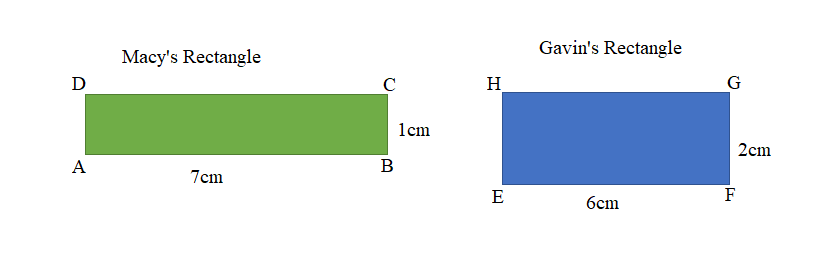
Area of the ABCD Macy’s rectangle = 7 Square cm.
Perimeter of the ABCD Macy’s rectangle = 16cms.
Area of the EFGH Gavin’s rectangle = 12 Square cm.
Perimeter of the EFGH Gavin’s rectangle = 16cms.
Here, Macy and Gavin has drawn two different rectangles with different lengths perimeters same 16cms yet different areas. Well, its possible to draw as many as rectangles with perimeters of 16 centimeters but different areas.
Explanation:

Figure1: Macy’s rectangle:
Length of the ABCD Macy’s rectangle = 7cm
Width of the ABCD Macy’s rectangle = 1cm
Area of the ABCD Macy’s rectangle = Length × Width
= 7cm × 1cm
= 7 Square cm.
Perimeter of the ABCD Macy’s rectangle = 2 ( Length + Width )
= 2 ( 7cm + 1cm)
= 2 × 8cm
= 16 cms.
Figure2: Gavin’s rectangle:
Length of the EFGH Gavin’s rectangle = 7cm
Width of the EFGH Gavin’s rectangle = 1cm
Area of the EFGH Gavin’s rectangle = Length × Width
= 6cm × 2cm
= 12 Square cm.
Perimeter of the EFGH Gavin’s rectangle = 2 ( Length + Width )
= 2 ( 6cm + 2cm)
= 2 × 8cm
= 16 cms .
Eureka Math Grade 3 Module 7 Lesson 21 Exit Ticket Answer Key
On the grid below, shade and label at least two different rectangles with a perimeter of 20 centimeters.

Answer:
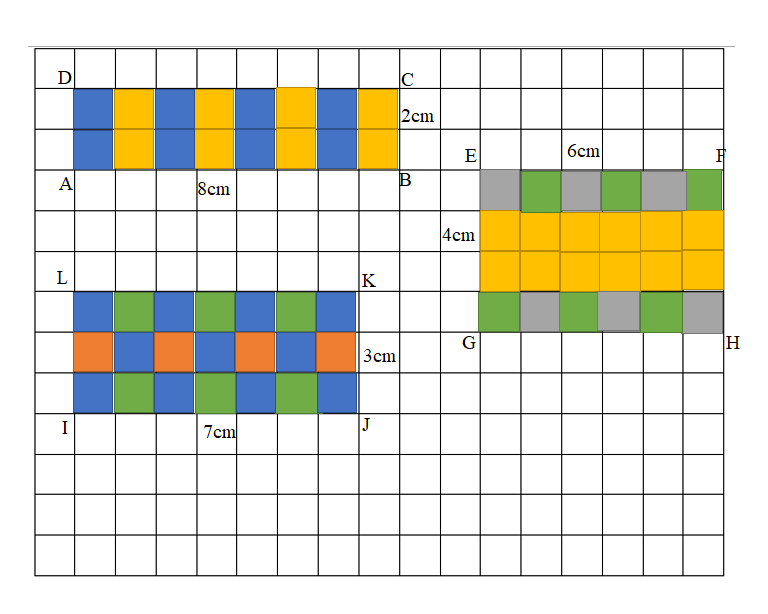
Explanation:
I have drawn three rectangles having lengths as ABCD Rectangle ( 8cm,2cm) , EFGH Rectangle ( 6cm,4cm) and IJKL Rectangle ( 7cm,3cm).
Eureka Math Grade 3 Module 7 Lesson 21 Homework Answer Key
Question 1.
Margo finds as many rectangles as she can with a perimeter of 14 centimeters.
a. Shade Margo’s rectangles on the grid below. Label the length and width of each rectangle.

b. Find the areas of the rectangles in part (a) above.
c. The perimeters of the rectangles are the same. What do you notice about the areas?
Answer:
a. 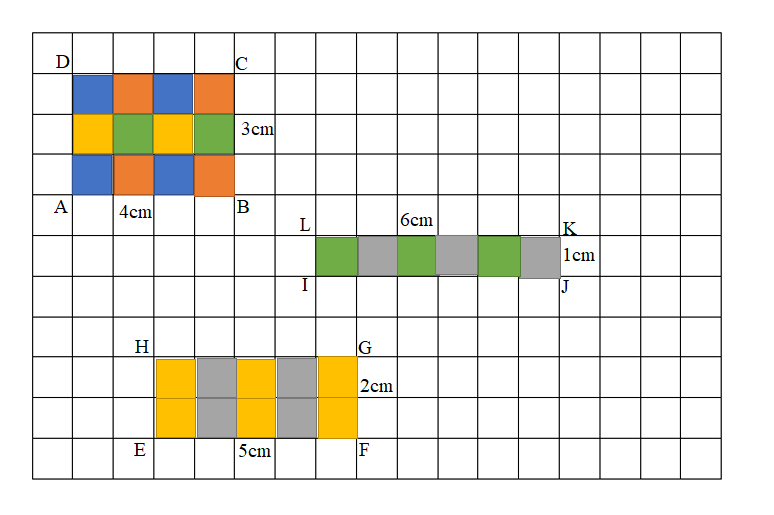
b. Area of the ABCD Rectangle = 12 square cm.
Area of the EFGH Rectangle = 10 square cm.
Area of the IJKL Rectangle = 6 square cm.
c. Perimeters of the three rectangles are the same having 14 cms, where as their areas are completely different from each other.
Explanation:
a.

b. Figure 1 : ABCD Rectangle
Length of the ABCD Rectangle = 4cm
Width of the ABCD Rectangle = 3cm
Area of the ABCD Rectangle = Length × Width
= 4cm × 3cm
= 12 square cm.
Figure 2 : EFGH Rectangle
Length of the EFGH Rectangle = 5cm
Width of the EFGH Rectangle = 2cm
Area of the EFGH Rectangle = Length × Width
= 5cm × 2cm
= 10 square cm.
Figure 3 : IJKL Rectangle
Length of the IJKL Rectangle = 6cm
Width of the IJKL Rectangle = 1cm
Area of the IJKL Rectangle = Length × Width
= 6cm × 1cm
= 6 square cm.
c. Perimeter of the ABCD rectangle = 2 ( Length + Width )
= 2 ( 4cm + 3cm)
= 2 × 7cm
= 14 cms.
Perimeter of the EFGH rectangle = 2 ( Length + Width )
= 2 ( 5cm + 2cm)
= 2 × 7cm
= 14 cms.
Perimeter of the IJKL rectangle = 2 ( Length + Width )
= 2 ( 6cm + 1cm)
= 2 × 7cm
= 14 cms.
Perimeters of the three rectangles are the same having 14 cms, where as their areas are completely different from each other.
Perimeter requires only the lengths of the four sides of rectangle to be added where as for area we require length and width of the rectangle.
Question 2.
Tanner uses unit squares to build rectangles that have a perimeter of 18 units. He creates the chart below to record his findings.
a. Complete Tanner’s chart. You might not use all the spaces in the chart.
| Perimeter = 18 units Number of rectangles I made: _____ |
||
| Width | Length | Area |
| 1 unit | 8 units | 8 square units |
| 2 unit | 7 unit | 14 square units |
| 3 unit | 6 unit | 18 square units |
| 4 unit | 5 unit | 20 square units |
b. Explain how you found the widths and lengths in the chart above.
Answer:
The chart in itself has the labelling heading of the columns as length and width and their areas.
If not always length value is going to be more than the value of width in the measurements of rectangle.
Explanation:
The chart in itself has the labelling heading of the columns as length and width and their areas. If not always length value is going to be more than the value of width in the measurements of rectangle. This is how I found the widths and lengths in the chart above.
Question 3.
Jason and Dina both draw rectangles with perimeters of 12 centimeters, but their rectangles have different areas. Explain with words, pictures, and numbers how this is possible.
Answer:
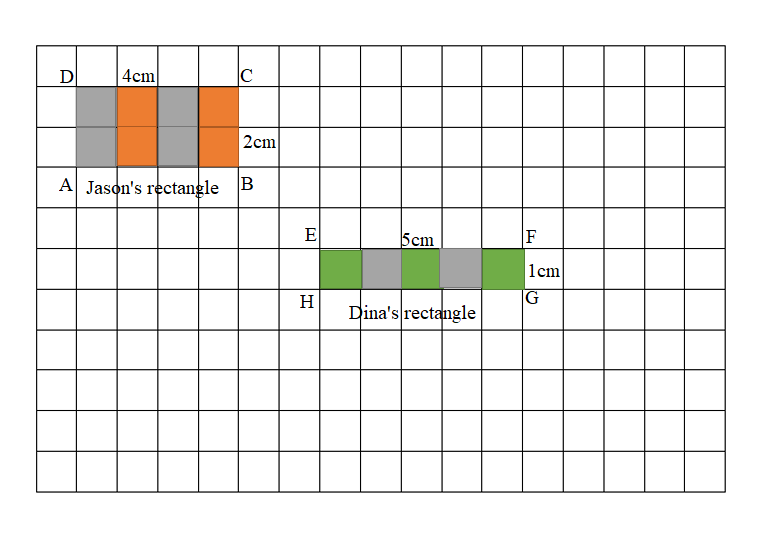
Area of the Jason’s ABCD Rectangle = 8 square cm.
Perimeter of the Jason’s ABCD Rectangle = 12 cm.
Area of the Dina’s EFGH Rectangle = 5 square cm.
Perimeter of the Dina’s EFGH Rectangle = 12 cm.
Perimeter requires only the lengths of the four sides of rectangle to be added where as for area we require length and width of the rectangle. Jason’s ABCD rectangle and Dina’s EFGH rectangle are having same perimeter yet different areas.
Explanation:
Jason’s ABCD Rectangle:
Length of the Jason’s ABCD Rectangle = 4cm
Width of the Jason’s ABCD Rectangle = 2cm
Area of the Jason’s ABCD Rectangle = Length × Width
= 4cm × 2cm
= 8 square cm.
Perimeter of the Jason’s ABCD Rectangle = 2 ( Length + Width )
= 2 ( 4cm + 2cm )
= 2 × 6cm
= 12 cm.
Dina’s EFGH Rectangle:
Length of the Dina’s EFGH Rectangle = 5cm
Width of the Dina’s EFGH Rectangle = 1cm
Area of the Dina’s EFGH Rectangle = Length × Width
= 5cm × 1cm
= 5 square cm.
Perimeter of the Dina’s EFGH Rectangle = 2 ( Length + Width )
= 2 ( 5cm + 1cm )
= 2 × 6cm
= 12 cm.
Jason’s ABCD rectangle and Dina’s EFGH rectangle are having same perimeter yet different areas.
Eureka Math Grade 3 Module 7 Lesson 21 Data Sheet Answer Key
Use the data you gathered from Problem Sets 20 and 21 to complete the charts to show how many rectangles you can create with a given perimeter. You might not use all the spaces in the charts.
| Perimeter = 10 units Number of rectangles you made: _1____ |
||
| Width | Length | Area |
| 1 unit | 4 units | 4 square units |
| 2 units | 3 units | 6 square units |
| Perimeter = 12 units Number of rectangles you made: _2____ |
||
| Width | Length | Area |
| 1 unit | 5 units | 5 square units |
| 2 units | 4 units | 8 square units |
| Perimeter = 14 units Number of rectangles you made: __3___ |
||
| Width | Length | Area |
| 1 unit | 6 units | 6 square units |
| 2 units | 5 units | 10 square units |
| 3 units | 4 units | 12 square units |
| Perimeter = 16 units Number of rectangles you made: __4___ |
||
| Width | Length | Area |
| 1 unit | 7 units | 7 square units |
| 2 units | 6 units | 12 square units |
| 3 units | 5 units | 15 square units |
| 4 units | 4 units | 16 square units |
| Perimeter = 18 units Number of rectangles you made: _4____ |
||
| Width | Length | Area |
| 1 unit | 8 units | 8 square units |
| 2 units | 7 units | 14 square units |
| 3 units | 6 units | 18 square units |
| 4 units | 5 units | 20 square units |
| Perimeter = 20 units Number of rectangles you made: __3___ |
||
| Width | Length | Area |
| 2 units | 8 units | 16 square units |
| 4 units | 6 units | 24 square units |
| 3 units | 7 units | 21 square units |