Fun learning activities are the best option to educate primary school students and make them understand the basic mathematical concepts like addition, subtraction, multiplication, division, etc. Grade 3 primary school students can find these fun-learning exercises for all math concepts through the Eureka Math Answers Grade 3 Common Core Curriculum.
Engage NY Eureka Math 3rd Grade Module 4 Lesson 9 Answer Key
You may have diverse opportunities to develop math skills and problem-solving skills but practicing with Eureka Math 3rd Grade Answer Key for better and efficient learning. Eureka Math Grade 3 provided Free Access Student Edition of Eureka Math Grade 3 Answers are enough to practice more and get a good grip on the subject. The diverse opportunities will develop problem-solving skills among the primary school kids Practising.
Eureka Math Grade 3 Module 4 Lesson 9 Problem Set Answer Key
Question 1.
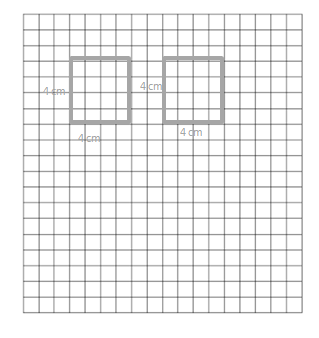
Cut the grid into 2 equal rectangles.
a. Draw and label the side lengths of the 2 rectangles.
Answer:
The side lengths of the two rectangles = 4 x 4 and 4 x 4.
Explanation:
In the above-given question,
given that,
cut the grid into two equal rectangles.
area of the rectangle = l x b.
where l = length and b = breadth.
area = 4 x 4.
area = 16.
so the side lengths of 2 rectangles = 4 x 4.
b. Write an equation to find the area of 1 of the rectangles.
Answer:
The area of the 1 of the rectangle = length x breadth.
Explanation:
In the above-given question,
given that,
area of the rectangle = l x b.
where l = length and b = breadth.
area = l x b.
c. Write an equation to show the total area of the 2 rectangles.
Answer:
The total area of the 2 rectangles = 16 sq cms.
Explanation:
In the above-given question,
given that,
area of the rectangle = l x b.
where l = length and b = breadth.
area = 4 x 4.
area = 16.
Question 2.
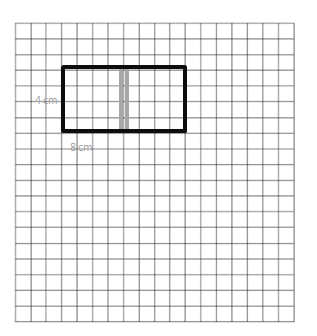
Place your 2 equal rectangles side by side to create a new, longer rectangle.
a. Draw an area model to show the new rectangle. Label the side lengths.
Answer:
The side lengths of the two rectangles = 4 cm x 8 cm.
Explanation:
In the above-given question,
given that,
cut the grid into two equal rectangles.
area of the rectangle = l x b.
where l = length and b = breadth.
area = 4 x 8.
area = 32.
so the side lengths of 2 rectangles = 4 x 8.
b. Find the total area of the longer rectangle.
Answer:
The total area of the longer rectangle = 32 sq cms.
Explanation:
In the above-given question,
given that,
area of the rectangle = l x b.
where l = length and b = breadth.
area = 4 x 8.
area = 32 sq cms.
Question 3.
Furaha and Rahema use square tiles to make the rectangles shown below.
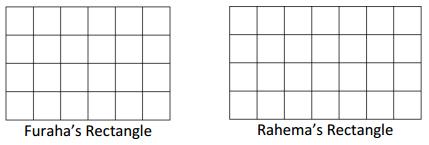
a. Label the side lengths on the rectangles above, and find the area of each rectangle.
Answer:
The side length of the Rahema rectangle = 4 cms x 6 cms.
Explanation:
In the above-given question,
given that,
area of the rectangle = l x b.
where l = length and b = breadth.
area = 4 x 6.
area = 24.
Answer:
The side length of the Rahema rectangle = 4 cms x 7 cms.
Explanation:
In the above-given question,
given that,
area of the rectangle = l x b.
where l = length and b = breadth.
area = 4 x 7.
area = 28.
b. Furaha pushes his rectangle next to Rahema’s rectangle to form a new, longer rectangle. Draw an area model to show the new rectangle. Label the side lengths.
Answer:
The side length of the Rahema rectangle = 4 cms x 8 cms.
Explanation:
In the above-given question,
given that,
area of the rectangle = l x b.
where l = length and b = breadth.
area = 4 x 8.
area = 32.
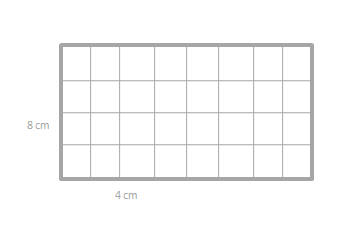
c. Rahema says the area of the new, longer rectangle is 52 square units. Is she right? Explain your answer.
Answer:
No, she was not correct.
Explanation:
given that,
area of the rectangle = l x b.
where l = length and b = breadth.
area = 4 x 8.
area = 32.
so the area of the rectangle = 32 sq units.
Question 4.
Kiera says she can find the area of the long rectangle below by adding the areas of Rectangles A and B. Is she right? Why or why not?
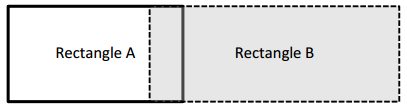
Answer:
Yes, she was correct.
Explanation:
In the above-given question,
given that,
Kiera says that she can find the area of the long rectangle below by adding the areas of the rectangles A and B.
area = l x b.
area of the rectangles A + B = rectangle C.
so she was correct.
Eureka Math Grade 3 Module 4 Lesson 9 Exit Ticket Answer Key
Lamar uses square tiles to make the 2 rectangles shown below.
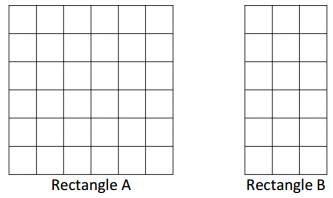
Question 1.
Label the side lengths of the 2 rectangles.
Answer:
The side lengths of rectangle A = 6 cm x 6 cm.
the side lengths of rectangle B = 6 cm x 3 cm.
Explanation:
In the above-given question,
given that,
area of the rectangle A = l x b.
where l = length and b = breadth.
area = 6 x 6.
area of the rectangle B = l x b.
where l = length and b = breadth.
area = 6 x 3.
Question 2.
Write equations to find the areas of the rectangles.
Area of Rectangle A: ______36_sq__cm______
Area of Rectangle B: ___18__sq__cm________
Answer:
The area of rectangle A = 36 sq cm.
the area of rectangle B = 18 sq cm.
Explanation:
In the above-given question,
given that,
area of the rectangle A = l x b.
where l = length and b = breadth.
area = 6 x 6.
area = 36 sq cm.
area of the rectangle B = l x b.
where l = length and b = breadth.
area = 6 x 3.
area = 18 sq cm.
Question 3.
Lamar pushes Rectangle A next to Rectangle B to make a bigger rectangle. What is the area of the bigger rectangle? How do you know?
Answer:
The area of the bigger rectangle = 6 cms x 9 cms.
Explanation:
In the above-given question,
given that,
area of the rectangle = l x b.
where l = length and b = breadth.
area = 6 x 9.
area = 54.
so the area of the bigger rectangle = 54 sq cms.
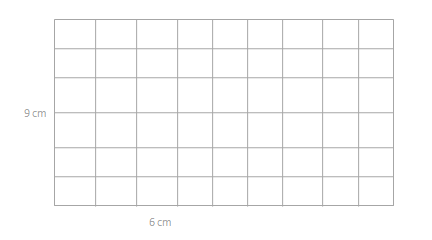
Eureka Math Grade 3 Module 4 Lesson 9 Homework Answer Key
Question 1.
Use the grid to answer the questions below.

a. Draw a line to divide the grid into 2 equal rectangles. Shade in 1 of the rectangles that you created.
Answer:
The area of the rectangle = 32 sq cms.
Explanation:
In the above-given question,
given that,
area of the rectangle = l x b.
where l = length and b = breadth.
area = 8 x 4.
area = 32 sq cm.
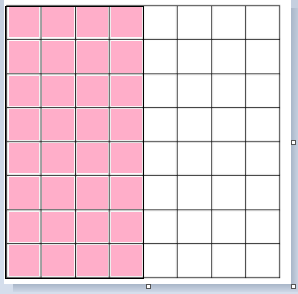
b. Label the side lengths of each rectangle.
Answer:
The side lengths of rectangle A = 8 cm x 4 cm.
the side lengths of rectangle B = 8 cm x 4 cm.
Explanation:
In the above-given question,
given that,
area of the rectangle A = l x b.
where l = length and b = breadth.
area = 8 x 4.
area = 32 sq cm.
area of the rectangle B = l x b.
where l = length and b = breadth.
area = 8 x 4.
area = 32 sq cm.
c. Write an equation to show the total area of the 2 rectangles.
Answer:
The area of rectangle A = 32 sq cm.
the area of rectangle B = 32 sq cm.
Explanation:
In the above-given question,
given that,
area of the rectangle A = l x b.
where l = length and b = breadth.
area = 8 x 4.
area = 32 sq cm.
area of the rectangle B = l x b.
where l = length and b = breadth.
area = 8 x 4.
area = 32 sq cm.
Question 2.
Alexa cuts out the 2 equal rectangles from Problem 1(a) and puts the two shorter sides together.
a. Draw Alexa’s new rectangle and label the side lengths below.
Answer:
The side lengths of the new rectangle = 4 cm x 4cm.
Explanation:
In the above-given question,
given that,
area of the rectangle = l x b.
where l = length and b = breadth.
area = 4 x 4.
area = 16 sq cm.
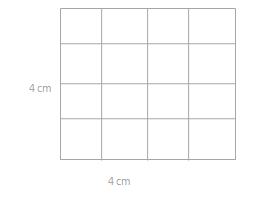
b. Find the total area of the new, longer rectangle.
Answer:
The area of the new rectangle = 16 sq cm.
Explanation:
In the above-given question,
given that,
area of the rectangle = l x b.
where l = length and b = breadth.
area = 4 x 4.
area = 16 sq cm.
c. Is the area of the new, longer rectangle equal to the total area in Problem 1(c)? Explain why or why not.
Answer:
No, the longer rectangle does not equal the total area in the problem.
Explanation:
In the above-given question,
given that,
the area of the longer rectangle = l x b.
where l = length and b = breadth.
area = 4 x 4.
area = 16 sq cm.
Eureka Math Grade 3 Module 4 Lesson 9 Template Answer Key
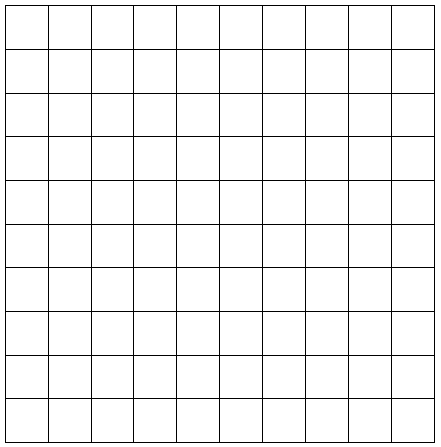
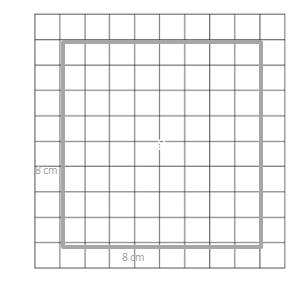
________64_sq_cm.____
small centimeter grid
Answer:
The area of the rectangle = 64 sq cm.
Explanation:
given that,
area of the rectangle = l x b.
where l = length and b = breadth.
area = 8 x 8.
area = 64.
so the area of the rectangle = 64 sq cm.