Engage NY Eureka Math Geometry Module 4 Lesson 14 Answer Key
Eureka Math Geometry Module 4 Lesson 14 Example Answer Key
Example 1.
Programmers want to program a robot so that it moves at a uniform speed along a straight line segment connecting two points A and B. If A(0, -1) and B(1, 1), and the robot travels from A to B in 1 minute,
a. Where is the robot at t = 0?
Answer:
The robot will be at A(0, -1).
b. Where is the robot at t = 1?
Answer:
The robot will be at B(1, 1).
c. Draw a picture that shows where the robot will be at 0 ≤ t ≤ 1.
Answer:
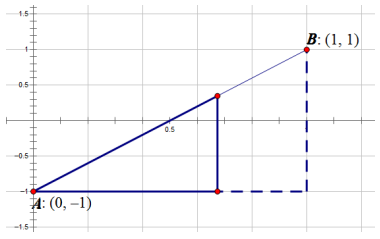
Student pictures will vary, but they should all include similar right triangles. Students should look around the room at the triangles their fellow students sketched.
Example 2.
Our robot has been reprogrammed so that it moves along the same straight line path through two points A(0, -1) and B(1, 1) at a uniform rate but makes the trip in 0. 6 minutes instead of 1 minute.
How does this change the way we calculate the location of the robot at any time, t?
a. Find the location, P, of the robot from Example 1 If the robot were traveling at a uniform speed that allowed It to make the trip from A to B in 0.6 minutes. Is the robot’s speed greater or less than the robot’s speed In Example 1?
Answer:
P = (a1, a2) + \(\frac{t}{0.6}\) (b1 – a1, b2 – a2) or P = (a1, a2) + \(\frac{5}{3}\)t(b1 – a1, b2 – a2)
The robot is moving faster than it was in Example 1 because it travels the same distance from A and B in a shorter period of time.
b. Find the location, P, of the robot from Example 1 if the robot were traveling at a uniform speed that allowed It to make the trip from A to B in 1. 5 minutes. Is the robot’s speed greater or less than the robot’s speed in Example 1?
Answer:
P = (a1, a2) + \(\frac{t}{1.5}\) (b1 – a1, b2 – a2) or P = (a1, a2) + \(\frac{2}{3}\)t(b1 – a1, b2 – a2)
The robot is moving more slowly than it was in Example 1 because it travels the same distance from A and B in a longer period of time.
Example 3.
A programmer wants to program a robot so that it moves at a constant speed along a straight line segment connecting the point A(30, 60) to the point 8(200, 100) over the course of a minute.
At time t = 0, the robot is at point A.
At time t = 1, the robot is at point B.
a. Where will the robot be at time t = \(\frac{1}{2}\)?
Answer:
Because the robot is moving at a uniform speed, the robot should travel half the distance between points A and B in half of the time it takes the robot to travel the entire distance.
30 + \(\frac{1}{2}\)(200 – 30)60 + \(\frac{1}{2}\)(100 – 60)) = (115, 80)
b. Where will the robot be at time t = 0.6?
Answer:
The robot will be three-fifths of the way along the segment from A to B.
(30 + \(\frac{3}{5}\)(200 – 30), 60 + \(\frac{3}{5}\)(100 – 60)) = (132, 84)
Eureka Math Geometry Module 4 Lesson 14 Opening Exercise Answer Key
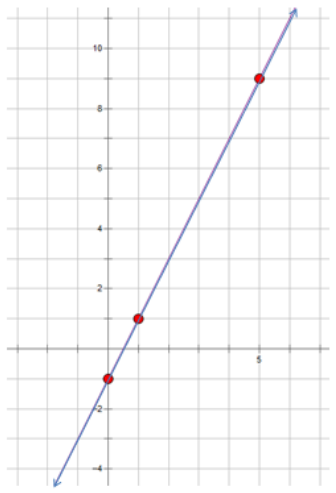
a. If f(t) = (t, 2t – 1), find the values of f(0), f(1), and f(5), and plot them on a coordinate plane.
Answer:
f(0) = (0, -1)
f(1) = (1, 1)
f(S) = (5, 9)
b. What is the image of f(t)?
Answer:
A line
c. At what time does the graph of the line pass through the y- axis?
Answer:
The line passes through the y-axis when t = 0.
d. When does it pass through the x-axis?
Answer:
The line passes through the x-axis when 2t – 1 = 0 or when t = \(\frac{1}{2}\).
e. Can you write the equation of the line you graphed in slope y-intercept form?
Answer:
y = 2x – 1
f. How does this equation compare with the definition of f(t)?
Answer:
The value of the second coordinate is obtained by taking two times the value of the first coordinate and then subtracting 1.
Eureka Math Geometry Module 4 Lesson 14 Exercise Answer Key
A robot is programmed to move along a straight line path through two points A and B. It travels at a uniform speed that allows It to make the trip from A(0, -1) to B(1, 1) In 1 minute. Find the robot’s location, P, for each time t in minutes.
a. t = \(\frac{1}{4}\)
Answer:
(0 + \(\frac{1}{4}\) (1 – 0), – 1 + \(\frac{1}{4}\) (1 – (1)))
(\(\frac{1}{4}\), – \(\frac{1}{2}\))
b. t = 0.7
Answer:
(0 + 0.7(1 – 0), -1 + 0.7(1 (-1)))
(0.7, 0.4)
c. t = \(\frac{5}{4}\)
Answer:
(0 + \(\frac{5}{4}\)(1 – 0), -1 + \(\frac{5}{4}\)(1 – (-1))
(\(\frac{5}{4}\), \(\frac{3}{2}\))
d. t = 2.2
Answer:
(0 + 2.2(1 – 0), – 1 + 2.2(1 – (-1)))
(2.2, 3.4)
Exercise 2.
Two robots are moving along straight line paths in a rectangular room. Robot 1 starts at point A(20, 10) and travels at a constant speed to point B(120, 50) in 2 minutes. Robot 2 starts at point C(90, 10) and travels at a constant speed to point D(60, 70) in 90 seconds.
a. Find the location, P, of Robot 1 after it has traveled for t minutes along its path from A to B.
Answer:
p = (20 + \(\frac{t}{2}\)(100), 10 + \(\frac{t}{2}\)(4o))
P = (20, 10) + \(\frac{t}{2}\)(100, 40)
b. Find the location, Q, of Robot 2 after It has traveled for t minutes along its path from C to D.
Answer:
Q = 90 + \(\frac{t}{1.5}\)(-30), 10 + \(\frac{t}{1.5}\)(60)
Q = (90, 10) + \(\frac{t}{1.5}\)(-3o, 60)
c. Are the robots traveling at the same speed? If not, which robot’s speed is greater?
Answer:
AB CD
AB = \(\sqrt{11600}\) CD = \(\sqrt{4500}\)
AB = 20√29 CD = 30√5
AB ≈ 107.7 CD ≈ 67.1
Robot 1 travels approximately 107.7 units in two minutes, which is about 53.85 units per minute. Robot 2 travels approximately 67. 1 units in 1.5 minutes, which Is about 44.7 units per minute. Therefore, Robot 1’s speed is greater.
d. Are the straight line paths that the robots are traveling parallel, perpendicular, or neither? Explain your answer.
Answer:
slope \(\overline{A B}\) = \(\frac{50-10}{120-20}\) = \(\frac{2}{5}\)
slope \(\overline{C D}\) = \(\frac{70-10}{60-90}\) = – 2
The paths are neither parallel nor perpendicular; the slopes of their straight line paths are not equal nor do they have a product equal to -1.
Eureka Math Geometry Module 4 Lesson 14 Problem Set Answer Key
Question 1.
Find the coordinates of the intersection of the medians of ∆ ABC given A(2, 4), B(- 4, 0), and C(3, – 1).
Answer:
(\(\frac{1}{3}\)(2 + (- 4) + 3), (\(\frac{1}{3}\)(4 + 0 + (-1))) = ((\(\frac{1}{3}\), 1)
Question 2.
Given a quadrilateral with vertices A(-1, 3), B(1, 5), C(5, 1), and D(3, -1):
a. Prove that quadrilateral ABCD is a rectangle.
Answer:
\(\overline{A B}\) and \(\overline{D C}\) have slopes of 1, so they are parallel.
\(\overline{B C}\) and \(\overline{A D}\) have slopes of -1, so they are parallel.
Since adjacent sides have slopes that are negative reciprocals, they are perpendicular; therefore, each angle is a right angle.
Both pairs of opposite sides are parallel, so the quadrilateral is a parallelogram.
All angles are right angles, so the parallelogram is a rectangle.
b. Prove that (2,2) is a point on both diagonals of the quadrilateral.
Answer:
Since ABCD is a parallelogram, Its diagonals intersect at their midpoints. (2, 2) is the midpoint of both \(\overline{A C}\) and \(\overline{B D}\), so it is a point on both diagonals.
Question 3.
A robot is programed to travel along a line segment at a constant speed. If P represents the robot’s position at any given time t in minutes:
P = (240,60) + \(\frac{t}{10}\)(100, 100),
a. What was the robot’s starting position?
Answer:
Starting position: (240,60) + \(\frac{0}{10}\)(100,100) or (240,60)
b. Where did the robot stop?
Answer:
Stopping position: (240,60) + \(\frac{10}{10}\)(100,100) or (340, 160)
c. How long did it take the robot to complete the entire journey?
Answer:
The robot will travel the entire length of the segment in 10 minutes.
d. Did the robot pass through the point (310, 130), and, if so, how long into its journey did the robot reach this position?
Answer:
There are a number of ways to answer part (d). The one most relevant to this lesson might be the following:
Find a time such that 240 + \(\frac{t}{10}\)(100) = 310, and 60 + \(\frac{t}{10}\)(100) = 130. The robot passed through the point (310, 130) when t = 7.
Question 4.
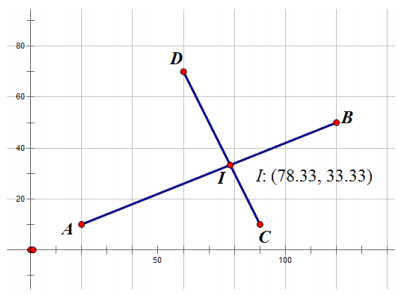
Two robots are moving along straight line paths in a rectangular room. Robot 1 starts at point A(20, 10) and travels at a constant speed to point B(120, 50) in two minutes. Robot 2 starts at point C(90, 10) and travels at a constant
speed to point D(60, 70) in 90 seconds. If the robots begin their journeys at the same time, will the robots collide? Why or why not?
Answer:
Robot 1’s position is modeled by
P = (20,10) + \(\frac{t}{2}\)(100, 40).
Robot 2’s position is modeled by
Q = (90,10) + \(\frac{t}{1.5}\)(- 30, 60).
(20, 10) + \(\frac{t}{2}\)(100, 40) = (78\(\frac{1}{32}\), 33\(\frac{1}{3}\))
Robot 1 passes through the point (78\(\frac{1}{3}\), 33\(\frac{1}{3}\)) at t = 1\(\frac{1}{6}\).
(90,10) + \(\frac{t}{1.5}\)(- 30, 60) = (78\(\frac{1}{3}\), 33\(\frac{1}{3}\))
Robot 2 passes through the point (78\(\frac{1}{3}\), 33\(\frac{1}{3}\)) at t = \(\frac{7}{12}\).
The paths of the two robots do intersect, but the robots reach this point (78\(\frac{1}{3}\), 33\(\frac{1}{3}\)) at different times, so the robots will not collide.
Eureka Math Geometry Module 4 Lesson 14 Exit Ticket Answer Key
Programmers want to program a robot so that it moves along a straight line segment connecting the point A(35, 80) to the point 8(150,15) at a uniform speed over the course of five minutes. Find the robot’s location at the following times (in minutes):
a. t = 0
Answer:
At t = 0, the robot is at point A(35, 80).
b. t = 2
Answer:
At t = 2, the robot is at (35, 80) + \(\frac{2}{5}\)(115, -65) or (81, 54).
c. t = 3.5
Answer:
At t = 3.5, the robot is at (35, 80) + \(\frac{3.5}{5}\)(115, -65) or (115.5, 34.5).
d. t = 5
Answer:
At t = 5, the robot is at point B(150, 15).